Марковская цепь — различия между версиями
Igusev (обсуждение | вклад) (Добавлен подсчет поглощающих состояний) |
|||
| Строка 121: | Строка 121: | ||
* поглощающим состоянием является состояние <tex> 5 </tex>. | * поглощающим состоянием является состояние <tex> 5 </tex>. | ||
* если расматривать <tex> \{6, 7\} </tex> отдельно, можно выделить два циклических класса <tex> \{6\} </tex> и <tex> \{7\} </tex> (на каждом шаге цепь переходит из одного состояния в другое, а через <tex> d = 2 </tex> шага возвращается в одно и то же состояние. | * если расматривать <tex> \{6, 7\} </tex> отдельно, можно выделить два циклических класса <tex> \{6\} </tex> и <tex> \{7\} </tex> (на каждом шаге цепь переходит из одного состояния в другое, а через <tex> d = 2 </tex> шага возвращается в одно и то же состояние. | ||
| + | |||
| + | ==Подсчет количества поглощащих состояний== | ||
| + | Пусть <tex>\mathtt{transition}</tex> — массив переходов марковской цепи, где <tex>\mathtt{transition[i][2]}</tex> — вероятность перехода из состояния <tex>\mathtt{transition[i][0]}</tex> в <tex>\mathtt{transition[i][1]}</tex>. | ||
| + | Тогда, по определению поглощающего состояния, если <tex>\mathtt{j}</tex> — поглощающее состояние, то <tex>\mathtt{transition[j][2] = 1}</tex>. По этому признаку помно определить все поглощающие состояния в цепи. | ||
| + | |||
| + | ===Псевдокод=== | ||
| + | *<tex>\mathtt{absorbing}: boolean:[\mathtt{n}]</tex> — массив состояний. Если i — посглощающее состояние absorbing[i] = true | ||
| + | *<tex>\mathtt{n}</tex> — количество состояний | ||
| + | *<tex>\mathtt{m}</tex> — количество переходов | ||
| + | |||
| + | '''function''' findAbsorbings(transition: '''int'''[m][2]): | ||
| + | '''boolean''' absorbing[m] | ||
| + | '''for''' i = 0 '''to''' m - 1 | ||
| + | '''if''' transition[i][0] == transition[i][1] '''and''' transition[i][2] == 1 | ||
| + | absorbing[transition[i][0]] = ''true'' | ||
| + | '''return''' absorbing | ||
== Литература == | == Литература == | ||
| Строка 127: | Строка 143: | ||
* Дж. Кемени, Дж. Снелл "Конечные цепи Маркова" | * Дж. Кемени, Дж. Снелл "Конечные цепи Маркова" | ||
* [http://ru.wikipedia.org/wiki/%D0%A6%D0%B5%D0%BF%D0%B8_%D0%9C%D0%B0%D1%80%D0%BA%D0%BE%D0%B2%D0%B0 Википедия — Цепь Маркова] | * [http://ru.wikipedia.org/wiki/%D0%A6%D0%B5%D0%BF%D0%B8_%D0%9C%D0%B0%D1%80%D0%BA%D0%BE%D0%B2%D0%B0 Википедия — Цепь Маркова] | ||
| + | *[https://en.wikipedia.org/wiki/Absorbing_Markov_chain Wikipedia — Absorbing Markov chain] | ||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
[[Категория: Марковские цепи ]] | [[Категория: Марковские цепи ]] | ||
Версия 09:06, 28 марта 2018
| Определение: |
| Цепь Маркова — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем, что при фиксированном настоящем будущее независимо от прошлого.
Процесс в каждый момент времени находится в одном из состояний. При этом, если он находится в состоянии с номером , то он перейдет в состояние с вероятностью . Матрицу называют матрицей переходов. |
На матрицу переходов накладываются следующие условия:
Такая матрица называется стохастической.
Марковскую цепь можно представить в виде графа, в котором вершины — это состояния процесса, а ребра — переходы между состояниями, и на ребре из в написана вероятность перехода из в , то есть .
Содержание
Распределение вероятностей
Марковскую цепь в любой момент времени можно охарактеризовать вектором-строкой — распределением вероятностей по состояниям цепи ( — вероятность цепи в момент времени быть в состоянии ).
Если — текущее распределение вероятностей, то можно узнать распределение на следующем шаге, умножив вектор на матрицу перехода:
.
Из ассоциативности произведения матриц следует, что для того, чтобы узнать распределение вероятностей через шагов, нужно умножить на матрицу перехода, возведённую в степень :
.
Для марковской цепи иногда задают начальное распределение , хотя во многих классах марковских цепей распределение по прошествии большого периода времени от него не зависит (такое распределение называют предельным).
Достижимость и сообщаемость
Обозначим вероятность попасть из состояния в состояние за переходов как .
| Определение: |
| Состояние достижимо (accesible) из состояния , если существует такое , что . Достижимость из обозначается . |
| Определение: |
| Состояния и сообщаются (communicate), если они достижимы друг из друга. Сообщаемость и обозначается . |
Классификация цепей и состояний
Неразложимая цепь
| Определение: |
| Неразложимый класс (communicating class) — класс эквивалентности множества состояний по отношению сообщаемости. Если представить марковскую цепь как граф, неразложимый класс будет аналогичен компоненте сильной связности. |
| Определение: |
| Неразложимая цепь (ireducible chain) — цепь Маркова, в которой все состояния образуют один неразложимый класс. |
Эргодическая цепь
| Определение: |
| Упорядочим (очевидно, упорядочение будет частичным) неразложимые классы отношением достижимости. Минимальные элементы в таком упорядочении называются эргодическими классами. Состояния в эргодических классах называются эргодическими (ergodic), возвратными, или существенными. Все остальные неразложимые классы называются невозвратными классами. Состояния, входящие в них, называются невозвратными или несущественными. |
| Определение: |
| Если эргодический класс состоит из одного состояния, такое состояние называется поглощающим (absorbing). |
Из свойств частичного упорядочения, в любой цепи Маркова найдется хотя бы один эргодический класс.
| Определение: |
| Эргодическая марковская цепь — марковская цепь, целиком состоящая из одного эргодического класса. |
Пусть — множество таких , что находясь в состоянии , можно оказаться в состоянии через шагов. — наибольший общий делитель чисел из множества .
| Лемма: |
Для и , принадлежащих одному классу эквивалентности, и числа из множества сравнимы между собой по модулю . |
| Доказательство: |
| Пусть . Из можно попасть в и обратно, значит, . Также после попадания в можно сколько угодно раз перейти из него в самого себя, и только потом перейти в , для этого понадобится шагов при любом достаточно большом . Значит, должно делиться на . Но аналогично можно доказать, что делится на , поэтому . Также можно перейти за шагов в , а потом попасть в , поэтому . Значит, и оба делятся на , то есть и сравнимы между собой по модулю . |
Введём числа , так, что любой элемент из сравним с по модулю .
| Определение: |
| Циклический класс — класс, для любых элементов и которого верно равенство . |
| Определение: |
| Если цепь состоит целиком из одного циклического класса, её называют регулярной, иначе — циклической. |
Если цепь циклическая, у неё есть некоторый период , а её состояния подразделяются на циклических классов. Цепь движется по циклическим классам в определённом порядке, возвращаясь в класс с начальным состоянием через шагов.
Поглощающая цепь
| Определение: |
| Поглощающее состояние — состояние, из которого нельзя попасть ни в какое другое, то есть — поглощающее состояние, если . |
| Определение: |
| Поглощающей (absorbing chain) называется марковская цепь, в которой есть хотя бы одно поглощающее состояние и из любого состояния достижимо хотя бы одно поглощающее. |
В примере на рисунке поглощающими являются состояния 3 и 4, а непоглощающими — 1 и 2.
Пример
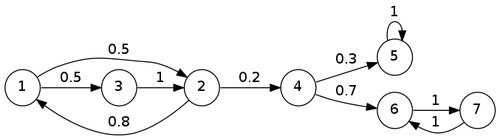
На рисунке:
- достижимыми состояниями являются: из (непосредственно), из (непосредственно), из (к примеру, через цепочку состояний ) и т.д.
- сообщаются состояния и (непосредственно), и (непосредственно), и (достижимы друг из друга) и т. д.
- неразложимыми классами являются множества вершин , , , ;
- эргодическими классами являются множества вершин , ;
- поглощающим состоянием является состояние .
- если расматривать отдельно, можно выделить два циклических класса и (на каждом шаге цепь переходит из одного состояния в другое, а через шага возвращается в одно и то же состояние.
Подсчет количества поглощащих состояний
Пусть — массив переходов марковской цепи, где — вероятность перехода из состояния в . Тогда, по определению поглощающего состояния, если — поглощающее состояние, то . По этому признаку помно определить все поглощающие состояния в цепи.
Псевдокод
- — массив состояний. Если i — посглощающее состояние absorbing[i] = true
- — количество состояний
- — количество переходов
function findAbsorbings(transition: int[m][2]):
boolean absorbing[m]
for i = 0 to m - 1
if transition[i][0] == transition[i][1] and transition[i][2] == 1
absorbing[transition[i][0]] = true
return absorbing
Литература
- И.В. Романовский «Дискретный анализ». 3-е изд., 2003. стр. 270—279
- Дж. Кемени, Дж. Снелл "Конечные цепи Маркова"
- Википедия — Цепь Маркова
- Wikipedia — Absorbing Markov chain