Производящие функции нескольких переменных — различия между версиями
(→Экспоненциальные производящие функции) |
(→Многочлены Бернулли) |
||
| Строка 118: | Строка 118: | ||
Экспоненциальная производящая функция для многочленов Бернулли имеет вид: | Экспоненциальная производящая функция для многочленов Бернулли имеет вид: | ||
| − | <tex>\mathcal{B}(x, s) = \sum\limits_{n=0}^{\infty}B_n(x)\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}e^{sx}</tex>. | + | <tex>\mathcal{B}(x, s) = \displaystyle\sum\limits_{n=0}^{\infty}B_n(x)\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}e^{sx}</tex>. |
| proof = | | proof = | ||
Для доказательства теоремы достаточно применить операцию усреднения к левой и правой частям равенства. С одной стороны, мы имеем: | Для доказательства теоремы достаточно применить операцию усреднения к левой и правой частям равенства. С одной стороны, мы имеем: | ||
| − | <tex>A(B(x, s)) = \sum\limits_{n=0}^{\infty}A(B_n(x))\dfrac{s^n}{n!} = \sum\limits_{n=0}^{\infty}x^n\dfrac{s^n}{n!} = e^{xs}</tex>. | + | <tex>A(B(x, s)) = \displaystyle\sum\limits_{n=0}^{\infty}A(B_n(x))\dfrac{s^n}{n!} = \sum\limits_{n=0}^{\infty}x^n\dfrac{s^n}{n!} = e^{xs}</tex>. |
С другой стороны, имеем: | С другой стороны, имеем: | ||
| Строка 137: | Строка 137: | ||
Доказанная теорема позволяет нам легко выписать экспоненциальную производящую функцию для чисел Бернулли. Для этого достаточно подставить в экспоненциальную производящую функцию для многочленов Бернулли значение <tex>x = 0</tex>: | Доказанная теорема позволяет нам легко выписать экспоненциальную производящую функцию для чисел Бернулли. Для этого достаточно подставить в экспоненциальную производящую функцию для многочленов Бернулли значение <tex>x = 0</tex>: | ||
| − | <tex>\sum\limits_{n=0} B_n\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}</tex>. | + | <tex>\displaystyle\sum\limits_{n=0} B_n\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}</tex>. |
==См. также== | ==См. также== | ||
Версия 22:30, 17 апреля 2018
| Определение: |
| Производящие функции нескольких переменных (англ. multivariable generating function) — обычные производящие функции, зависящие более, чем от одной переменной. Очень часто применяются функции от двух переменных (далее они и будут рассматриваться), которые в общем случае принимают вид: . |
Рассмотрим несколько примеров :
Содержание
Треугольник Паскаля
| Определение: |
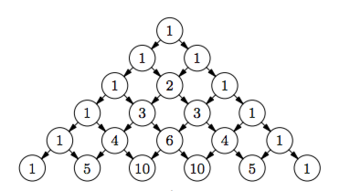
| Треугольник Паскаля (англ. Pascal's triangle) — бесконечная таблица биномиальных коэффициентов[1], имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. |
Элементы треугольника (рис.) перечисляют пути, идущие из его вершины в соответствующую клетку. Пути имеют вид ломаных, составленных из векторов единичной длины двух видов: идущих вправо-вниз и идущих влево-вниз.
Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию
Второй способ соответствует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис.) . Тогда производящая функция будет иметь вид
Также существует еще один способ: сопоставить треугольнику Паскаля экспоненциальную производящую функцию. Экспоненциальная производящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности , а числа .
Экспоненциальные производящие функции
Зафиксируем произвольную последовательность . Каждой последовательности мы можем сопоставить производящую функцию
определяемую последовательностью . Если в последовательности отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями, отвечающими последовательности . В зависимости от преследуемых целей могут принести и другие последовательности.
| Определение: |
| Производящие экспоненциальные функции (англ. exponential generating function) — функции, соответсвующие последовательности . |
| Определение: |
| Экспоненциальные производящие функции для целочисленных последовательностей называют функциями Гурвица (англ. Hurwitz function). |
Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операции над ними. Сумма ведет себя обычным образом:
а с произведением по-другому:
Коэффициенты произведения вычисляются по формуле
Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных и при интегрировании. Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их величины:
Обычная производящая функция выражается через экспоненциальную по формуле
Действительно,
Теперь можно выписать экспоненциальную производящую функцию для треугольника Паскаля:
Многочлены Бернулли
Для начала введен операцию усреднения, положив
.
Нетрудно заметить, что эта операция переводит многочлены в многочлены: она линейна, т.е. для любых постоянных и любых многочленов , а ее значение на мономе[2] равно
,
где многоточие обозначает слагаемые, степени которых меньше . Последняя формула показывает также, что преобразование переводит пространство многочленов степени не выше в себя, а значит, является линейным оператором в этом пространстве. Этот оператор обратим. Действительно, любой многочлен степени не выше может быть получен в результате усреднения многочлена такой же степени, и, используя последнюю формулу, мы заключаем, что и любой многочлен степени не выше является результатом усреднения некоторого многочлена степени не выше . Отметим, что при усреднении степень многочлена сохраняется.
| Определение: |
| Многочленом Бернулли (англ. Bernoulli polynomial) степени называется многочлен , результатом усреднения которого служит моном , т.е. . |
Первые многочлены Бернулли нетрудно сосчитать:
| Теорема (Экспоненциальная производящая функция для многочленов Бернулли): |
Экспоненциальная производящая функция для многочленов Бернулли имеет вид:
. |
| Доказательство: |
|
Для доказательства теоремы достаточно применить операцию усреднения к левой и правой частям равенства. С одной стороны, мы имеем: . С другой стороны, имеем: , и теорема доказана. |
Определим теперь числа Бернулли[3] как значения многочленов Бернулли в нуле. Вот начало последовательности чисел Бернулли:
Доказанная теорема позволяет нам легко выписать экспоненциальную производящую функцию для чисел Бернулли. Для этого достаточно подставить в экспоненциальную производящую функцию для многочленов Бернулли значение :
.
См. также
Примечания
Источники информации
- Ландо С. К., Лекции о производящих функциях. — 3-е изд., испр. — М.: МЦНМО, 2007. — 57с. ISBN 978-5-94057-042-4