Асимптотика гипергеометрических последовательностей — различия между версиями
Iksiygrik (обсуждение | вклад) м |
Iksiygrik (обсуждение | вклад) м |
||
| (не показано 47 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|id=def1. | |id=def1. | ||
| − | |definition= | + | |definition= |
| − | + | Последовательность, в которой отношение двух соседних членов равно отношению многочленов <tex>A(n)</tex> степени <tex>k</tex>, где <tex>k > 0</tex> и <tex>n</tex> - порядковый номер члена последовательности, называется '''гипергеометрической''' (англ. ''hypergeometric sequence''). | |
}} | }} | ||
| Строка 9: | Строка 9: | ||
|id=lemma1. | |id=lemma1. | ||
|statement= | |statement= | ||
| − | Пусть последовательность <tex>a_0,a_1, | + | Пусть последовательность <tex>a_0, a_1, \ldots</tex> положительных чисел такова, что <tex>\cfrac{a_{n+1}}{a_n}=A\cfrac{n^k + \alpha_1 \cdot n^{k-1} + \ldots + \alpha_k}{n^k+ \beta_1 \cdot n^{k-1}+ \ldots +\beta_k}</tex> для всех достаточно больших <tex>n</tex>, причем <tex>\alpha_1 \ne \beta_1</tex>. Тогда <tex>a_n</tex> растет как <tex>a_n \sim c \cdot A^n \cdot n^{\alpha_1-\beta_1}</tex> для некоторой постоянной <tex>c>0</tex>. |
| + | <br> | ||
| + | '''Замечание:''' Предположения леммы не позволяют определить величину константы <tex>c</tex>. Действительно, умножив последовательность <tex>a_n</tex> на произвольную постоянную <tex>d > 0</tex>, мы получим новую последовательность с тем же отношением последовательных членов, константа <tex>c</tex> для которой увеличивается в <tex>d</tex> раз. | ||
| + | |||
|proof= | |proof= | ||
| − | + | Рассмотрим предел <tex>\lim\limits_{n \to \infty} {\cfrac{a_n}{A^n \cdot n^{\alpha_1-\beta_1}}}</tex>. При <tex>a_n \sim c \cdot A^n \cdot n^{\alpha_1-\beta_1}</tex> для некоторого <tex>c</tex> данный предел будет существовать и равен <tex>c</tex>. С другой стороны, из определения существования предела<ref>[https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%B4%D0%B5%D0%BB_%D1%87%D0%B8%D1%81%D0%BB%D0%BE%D0%B2%D0%BE%D0%B9_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D0%B8 Предел числовой последовательности]</ref> на бесконечности следует, что он равен некоторому <tex>c</tex>, то есть <tex>\lim\limits_{n \to \infty} {\cfrac{a_n}{A^n \cdot n^{\alpha_1-\beta_1}}} = c</tex>. Из чего можно сделать вывод, что утверждение леммы эквивалентно тому, что существует предел <tex>\lim\limits_{n \to \infty} {\cfrac{a_n}{A^n \cdot n^{\alpha_1-\beta_1}}}</tex>. <br> Прологарифмировав, мы приходим к необходимости доказать существование предела <tex>\lim\limits_{n \to \infty} {( \ln {a_n} - n \cdot \ln A - (\alpha_1 - \beta_1) \cdot \ln n )}</tex>. | |
| − | Для доказательства существования предела | + | Для доказательства существования предела применим критерий Коши<ref>[http://nuclphys.sinp.msu.ru/mathan/p1/m0509.html Критерий Коши]</ref>, т. е. будем доказывать, что рассматриваемая последовательность фундаментальна<ref>[https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%B4%D0%B0%D0%BC%D0%B5%D0%BD%D1%82%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%8C Фундаментальная последовательность]</ref>. |
| + | |||
| + | Перепишем отношение <tex>\cfrac{a_{n+1}}{a_n}</tex> в виде | ||
| + | |||
| + | <tex>\cfrac{a_{n+1}}{a_n}=A \cdot \cfrac{1 + \alpha_1 \cdot n^{-1} + \ldots + \alpha_k \cdot n^{-k}}{1 + \beta_1 \cdot n^{-1} + \ldots + \beta_k \cdot n^{-k}}=A \cdot f\left(\cfrac{1}{n}\right)</tex>, | ||
| + | |||
| + | где | ||
| − | <tex> | + | <tex>f(x)=\cfrac{1 + \alpha_1 \cdot x + \ldots + \alpha_k \cdot x^k}{1 + \beta_1 \cdot x + \ldots + \beta_k \cdot x^k}</tex> |
| − | + | Прологарифмировав отношение <tex>\cfrac{a_{n+1}}{a_n}</tex>, получаем | |
| − | <tex> | + | <tex>\ln a_{n+1} - \ln a_n = \ln A + \ln f\left(\cfrac{1}{n}\right)</tex>. |
| − | + | Посмотрим на функцию <tex>\ln f(x)</tex>. Выпишем начальные члены разложения функции <tex>f</tex> в ряд в точке <tex>0</tex>: | |
| − | <tex> | + | <tex>f(x)=1 + (\alpha_1 - \beta_1) \cdot x + \gamma \cdot x^2 + \ldots </tex> для некоторой константы <tex>\gamma</tex>. Это разложение - самый существенный элемент доказательства. Именно коэффициент <tex>\alpha_1 - \beta_1</tex>(отличный от нуля по предположению леммы) при линейном члене указывает на присутствие сомножителя <tex>n^{\alpha_1-\beta_1}</tex> в асимптотике. Для логарифма функции <tex>f</tex> имеем |
| − | + | <tex>\ln f(x)=(\alpha_1-\beta_1) \cdot x+\tilde{\gamma} \cdot x^2 + \ldots</tex> | |
| − | <tex>f(x) | + | Поэтому для некоторой постоянной <tex>C</tex> при достаточно маленьком <tex>x</tex> имеем <tex>|\ln f(x) - (\alpha_1 - \beta_1) \cdot x|<C \cdot x^2</tex>. В частности, если <tex>N</tex> достаточно велико, то <tex>∀ n>N</tex> получаем систему <tex>(*)</tex> |
| − | + | <tex> | |
| + | \begin{equation*} | ||
| + | \begin{cases} | ||
| + | \left| \ln a_{n+1} - \ln a_n - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n} \right| < C \cdot \cfrac{1}{n^2}, \\ | ||
| − | + | \left| \ln a_{n+2} - \ln a_{n+1} - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n+1} \right| < C \cdot \cfrac{1}{(n+1)^2}, \\ | |
| − | + | \ldots \\ | |
| − | + | \left| \ln a_{n+m} - \ln a_{n+m-1} - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n+m} \right| < C \cdot \cfrac{1}{(n+m)^2}. \\ | |
| + | \end{cases} | ||
| + | \end{equation*} | ||
| + | </tex> | ||
| − | <tex>|\ln a_{n+ | + | Теперь интересующее нас выражение в левой части неравенства <tex>|\ln a_{n+m} - \ln a_n - m \cdot \ln A - (\alpha_1 - \beta_1) \cdot \ln {(n + m)} + (\alpha_1 - \beta_1) \cdot \ln n| < ε </tex> можно оценить с помощью системы <tex>(*)</tex> и неравенства треугольника<ref>[https://ru.wikipedia.org/wiki/%D0%9D%D0%B5%D1%80%D0%B0%D0%B2%D0%B5%D0%BD%D1%81%D1%82%D0%B2%D0%BE_%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0 Неравенство треугольника]</ref>: |
| − | <tex>|\ln a_{n+ | + | <tex>\left| \ln a_{n+m} - \ln a_n - m \cdot \ln A - (\alpha_1 - \beta_1) \cdot ( \ln {(n+m)} - \ln n) \right| =</tex> |
| − | <tex> | + | <tex>= | \ln a_{n+m} - \ln a_{n + m - 1} + \ln a_{n + m - 1} - \ldots + \ln a_{n + 1} - \ln a_n - m \cdot \ln A - </tex> |
| − | <tex> | + | <tex> - (\alpha_1 - \beta_1) \cdot \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} + (\alpha_1 - \beta_1) \cdot \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - (\alpha_1 - \beta_1) \cdot (\ln {(n+m)} - \ln n) \Bigg| \leqslant</tex> |
| − | + | <tex>\leqslant \left| \ln a_{n+1} - \ln a_n - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n} \right| + \left| \ln a_{n+2} - \ln a_{n+1} - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n+1} \right| +</tex> | |
| − | <tex> | + | <tex>\ldots</tex> |
| − | <tex> | + | <tex>+ \left| \ln a_{n+m} - \ln a_{n+m-1} - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n+m} \right| + \left| \alpha_1 - \beta_1 \right| \cdot \left| \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n \right| \leqslant</tex> |
| − | <tex> | + | <tex>\leqslant C \cdot \left(\cfrac{1}{n^2} + \cfrac{1}{(n+1)^2} + \ldots + \cfrac{1}{(n+m-1)^2}\right) + \left| \alpha_1 - \beta_1 \right| \cdot \left| \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n \right|</tex>. |
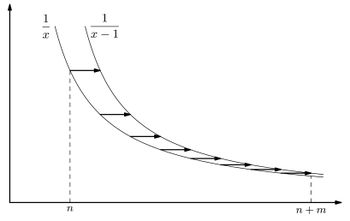
| − | <tex>\ | + | Поскольку ряд <tex>\sum\limits_{k=1}^{\infty} \cfrac{1}{k^2}</tex> сходится, первое слагаемое в правой части последнего неравенства при больших <tex>n</tex> можно сделать сколь угодно малым. Чтобы оценить второе слагаемое, заметим, что стоящая в нем сумма представляет собой площадь под графиком ступенчатой функции <tex>\cfrac{1}{[x]}</tex> на отрезке <tex>[n, n+m]</tex>, |
| − | + | [[Файл:InkedOiGdtVITsP10_LI.jpg|350px|thumb|right|График функции <tex>y = \cfrac{1}{[x]}</tex> на отрезке <tex>[n, n + m]</tex>]] | |
| − | |||
| − | + | (Здесь через <tex>[x]</tex> обозначена целая часть числа <tex>x</tex>, наибольшее целое число, не превосходящее <tex>x</tex>.) Эта площадь больше, чем площадь под графиком функции <tex>y = \cfrac{1}{x}</tex>, но меньше, чем площадь под графиком функции <tex>y = \cfrac{1}{x-1}</tex> на этом же отрезке. Площадь под графиком функции <tex>\cfrac {1}{x}</tex> равна <tex>\ln {(n + m)} - \ln {n}</tex>, площадь под графиком функции <tex>y = \cfrac{1}{x-1}</tex> равна <tex>\ln {(n+m-1)} - \ln {(n-1)}</tex>. Таким образом, интересующая нас разность не превосходит <tex>\left| (\ln {(n+m-1)} - \ln {(n-1)}) - \left( \ln {(n+m)} - \ln n \right) \right| =</tex> | |
| − | + | <tex>= \left| \ln {\cfrac {n+m-1}{n+m} - \ln {\cfrac {n-1}{n}}} \right| = </tex> | |
| + | <tex>= \left| \ln {\left(1 - \cfrac{1}{n+m}\right)} - \ln {\left(1 - \cfrac{1}{n}\right)} \right| <</tex> | ||
| − | + | <tex>< \left| \ln {\left(1 - \cfrac{1}{n}\right)} \right| < C \cdot \cfrac{1}{n}</tex>. | |
}} | }} | ||
| − | ''' | + | == Примеры == |
| + | '''Пример.''' Рассмотрим производящую функцию для [[Числа Каталана|чисел Каталана]] | ||
| + | |||
| + | <tex>A(s) = 1 + s + 2 \cdot s^2 + 5 \cdot s^3 + \ldots </tex> | ||
| + | |||
| + | Возведя ее в квадрат и умножив результат на s, получим | ||
| + | |||
| + | <tex>s \cdot A^2(s) = s + 2 \cdot s^2 + 5 \cdot s^3 + 14 \cdot s^4 + \ldots = A(s) - 1</tex>, | ||
| + | |||
| + | что дает нам квадратное уравнение на производящую функцию | ||
| + | |||
| + | <tex>s \cdot A^2(s) - A(s) + 1 = 0,</tex> | ||
| + | |||
| + | откуда | ||
| + | |||
| + | <tex>A(s) = \cfrac {1 - \sqrt {1 - 4 \cdot s}}{2 \cdot s}</tex> | ||
| + | |||
| + | Второй корень уравнения отбрасывается, так как <tex>\cfrac {1 + \sqrt {1 - 4 \cdot s}}{2 \cdot s} = \cfrac {1}{s} + \ldots</tex> содержит отрицательные степени <tex>s</tex> | ||
| + | |||
| + | Найденная производящая функция позволяет найти явную форму для [[Числа Каталана|чисел Каталана]]. Согласно биному Ньютона <ref>[https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0 Бином Ньютона]</ref> | ||
| − | == | + | <tex>a_n = \cfrac {\cfrac {1}{2} \cdot \cfrac {1}{2} \cdot \cfrac {3}{2} \cdot \ldots \cdot \cfrac {2 \cdot n - 1}{2} \cdot 4^{n + 1}}{2 \cdot (n + 1)!},</tex> |
| − | + | ||
| + | откуда, умножая на числитель и знаменатель на <tex>n!</tex> и сокращая на <tex>2^{n + 1}</tex>, получаем | ||
| + | |||
| + | <tex>a_n = \cfrac {(2 \cdot n)!}{n! \cdot (n + 1)!} = \cfrac {1}{n + 1} \cdot \dbinom {2 \cdot n}{n}</tex> | ||
| + | |||
| + | Последняя формула дает и более простое рекурсивное соотношение для [[Числа Каталана|чисел Каталана]]: | ||
| − | <tex>\ | + | <tex>\cfrac{c_{n+1}}{c_n}=\cfrac{4 \cdot n + 2}{n+2}=4 \cdot \cfrac{ n + \cfrac{1}{2}}{n+2}</tex> |
| − | Поэтому <tex>c_n \sim c \cdot 4^n \cdot n^{-\ | + | Поэтому <tex>c_n \sim c \cdot 4^n \cdot n^{-\dfrac{3}{2}}</tex> для некоторой постоянной <tex>c</tex>. |
'''Пример.''' Найдем асимптотику коэффициентов для функции <tex>(a-s)^{\alpha}</tex>, где <tex>\alpha</tex> вещественно. В ряде случаев эта асимптотика нам | '''Пример.''' Найдем асимптотику коэффициентов для функции <tex>(a-s)^{\alpha}</tex>, где <tex>\alpha</tex> вещественно. В ряде случаев эта асимптотика нам | ||
уже известна, например, при <tex>\alpha=−1</tex>. Согласно определению функции <tex>(1-s)^{\alpha}</tex> имеем | уже известна, например, при <tex>\alpha=−1</tex>. Согласно определению функции <tex>(1-s)^{\alpha}</tex> имеем | ||
| − | <tex>(a-s)^{\alpha}=a^{\alpha}(1-\ | + | <tex>(a-s)^{\alpha}=a^{\alpha} \cdot \left(1-\cfrac{s}{a}\right)^{\alpha}=a^{\alpha} \cdot \left(1 - \cfrac{\alpha}{1!} \cdot \cfrac{s}{a} + \cfrac{\alpha \cdot (\alpha-1)}{2!} \cdot {\left(\cfrac{s}{a}\right)^2} - \cfrac{\alpha \cdot (\alpha-1) \cdot (\alpha-2)}{3!} \cdot \left(\cfrac{s}{a}\right)^3 + \ldots \right)</tex> |
| − | Если <tex>\alpha</tex> — целое неотрицательное число, то ряд обрывается и вопроса об асимптотике не возникает. В противном случае начиная с некоторого номера все коэффициенты ряда имеют одинаковый знак. Для определения асимптотики мы можем воспользоваться | + | Если <tex>\alpha</tex> — целое неотрицательное число, то ряд обрывается и вопроса об асимптотике не возникает. В противном случае, начиная с некоторого номера, все коэффициенты ряда имеют одинаковый знак. Для определения асимптотики мы можем воспользоваться леммой при <tex>a_n=(-1)^n \cdot \cfrac{\alpha \cdot (\alpha-1) \cdot \ldots \cdot (\alpha-n+1)}{n! \cdot {\alpha}^n}:</tex> |
| − | <tex>\ | + | <tex>\cfrac{a_{n+1}}{a_n}=\cfrac{1}{a} \cdot \cfrac{n-\alpha}{n+1}</tex> |
| − | Поэтому <tex>a_n \sim c \cdot a^{-n} \cdot n^{-\alpha-1}</tex>. Например, коэффициенты функции <tex>-(1- | + | Поэтому <tex>a_n \sim c \cdot a^{-n} \cdot n^{-\alpha-1}</tex>. Например, коэффициенты функции <tex>-(1-4 \cdot s)^{\dfrac{1}{2}}</tex> ведут себя как <tex>c \cdot 4^n \cdot n^{-\dfrac{3}{2}}</tex>, и мы получаем повторный вывод ассимптотики для [[Числа Каталана|чисел Каталана]]. |
== См. также == | == См. также == | ||
* [[Производящая функция]] | * [[Производящая функция]] | ||
| + | * [[Числа Каталана]] | ||
==Примечания== | ==Примечания== | ||
Версия 16:26, 11 июня 2018
| Определение: |
| Последовательность, в которой отношение двух соседних членов равно отношению многочленов степени , где и - порядковый номер члена последовательности, называется гипергеометрической (англ. hypergeometric sequence). |
Вычисление асимптотики
| Лемма: |
Пусть последовательность положительных чисел такова, что для всех достаточно больших , причем . Тогда растет как для некоторой постоянной .
|
| Доказательство: |
|
Рассмотрим предел . При для некоторого данный предел будет существовать и равен . С другой стороны, из определения существования предела[1] на бесконечности следует, что он равен некоторому , то есть . Из чего можно сделать вывод, что утверждение леммы эквивалентно тому, что существует предел . Для доказательства существования предела применим критерий Коши[2], т. е. будем доказывать, что рассматриваемая последовательность фундаментальна[3]. Перепишем отношение в виде , где
Прологарифмировав отношение , получаем . Посмотрим на функцию . Выпишем начальные члены разложения функции в ряд в точке : для некоторой константы . Это разложение - самый существенный элемент доказательства. Именно коэффициент (отличный от нуля по предположению леммы) при линейном члене указывает на присутствие сомножителя в асимптотике. Для логарифма функции имеем
Поэтому для некоторой постоянной при достаточно маленьком имеем . В частности, если достаточно велико, то получаем систему
Теперь интересующее нас выражение в левой части неравенства можно оценить с помощью системы и неравенства треугольника[4]:
. Поскольку ряд сходится, первое слагаемое в правой части последнего неравенства при больших можно сделать сколь угодно малым. Чтобы оценить второе слагаемое, заметим, что стоящая в нем сумма представляет собой площадь под графиком ступенчатой функции на отрезке ,
. |
Примеры
Пример. Рассмотрим производящую функцию для чисел Каталана
Возведя ее в квадрат и умножив результат на s, получим
,
что дает нам квадратное уравнение на производящую функцию
откуда
Второй корень уравнения отбрасывается, так как содержит отрицательные степени
Найденная производящая функция позволяет найти явную форму для чисел Каталана. Согласно биному Ньютона [5]
откуда, умножая на числитель и знаменатель на и сокращая на , получаем
Последняя формула дает и более простое рекурсивное соотношение для чисел Каталана:
Поэтому для некоторой постоянной .
Пример. Найдем асимптотику коэффициентов для функции , где вещественно. В ряде случаев эта асимптотика нам уже известна, например, при . Согласно определению функции имеем
Если — целое неотрицательное число, то ряд обрывается и вопроса об асимптотике не возникает. В противном случае, начиная с некоторого номера, все коэффициенты ряда имеют одинаковый знак. Для определения асимптотики мы можем воспользоваться леммой при
Поэтому . Например, коэффициенты функции ведут себя как , и мы получаем повторный вывод ассимптотики для чисел Каталана.