Теорема Гринберга

Базовые определения

Определение:

Подграф (англ. subgraph) исходного графа — граф, содержащий некое подмножество вершин данного графа и некое подмножество инцидентных им рёбер. По отношению к подграфу исходный граф называется суперграфом.

Определение:

Порождённый подграф (англ. induced subgraph) — подграф, порождённый множеством рёбер исходного графа. Содержит не обязательно все вершины графа, но эти вершины соединены такими же ребрами, как в графе.

Определение:

Разрез графа — множество рёбер [math]E(V_1, V_2)[/math] (все рёбра между [math]V_1[/math] и [math]V_2[/math]) для произвольного разбиения [math]V(G)[/math] на два непересекающихся множества вершин [math]V_1[/math] и [math]V_2[/math].

Определение:

Бонд графа — это минимальный (по включению) непустой разрез графа [math]G[/math].

Лемма:

Разрез [math]E(V_1, V_2)[/math] связного графа [math]G[/math] является бондом, если и только если оба графа [math]G(V_1)[/math] и [math]G(V_2)[/math] связны.

Доказательство:

[math]\triangleright[/math]

Для удобства примем [math]E = E(V_1, V_2)[/math]. [math]\Rightarrow[/math]. Пусть [math]E[/math] - бонд. Докажем, что для любого ребра [math]e \in E[/math] граф [math]G - E + e[/math] связен. Действительно, пусть этот граф несвязен и имеет, скажем, компоненты связности [math]U_1[/math] и [math]U_2[/math]. Тогда [math]E \supsetneq E(U_1, U_2)[/math], а из связности графа [math]G[/math] следует, что [math]E(U_1, U_2) \neq \varnothing[/math]. Противоречие с минимальностью [math]E[/math]. Так как для любого ребра [math]e \in E = E(V_1, V_2)[/math] граф [math]G − E + e[/math] связен, оба графа [math]G(V_1)[/math] и [math]G(V_2)[/math] связны. [math]\Leftarrow[/math]. Если оба графа [math]G(V_1)[/math] и [math]G(V_2)[/math] — связны, то добавление любого ребра из [math]E[/math] даст нам связный подграф графа [math]G[/math]. Значит, в этом случае разрез [math]E[/math] минимален по включению. В силу связности [math]G[/math] этот разрез непуст, то есть, является бондом.

[math]\triangleleft[/math]

Определение:

Подграфы [math]V_1[/math] и [math]V_2[/math] из предыдущей леммы называются торцевыми графами.

Также стоит отметить, что если граф [math] G [/math] несвязен, то его бонд определим как бонд какой-либо его компоненты, а всякий перешеек графа образует однореберный бонд. Торцевые графы перешейка являются торцевыми графами соответствующего бонда.

Определение:

Гамильтоновым бондом (англ. hamiltonian bond) называется бонд графа [math] G [/math], торцевыми графами которого являются деревья.

Теорема Гринберга

Теорема (Гринберг):

Пусть связный граф [math] G [/math] имеет гамильтонов бонд [math] H [/math] с торцевыми графами [math] X [/math] и [math] Y [/math]. Пусть [math] f_n^{X} [/math] и [math] f_n^{Y} [/math] — число вершин в графов [math] X [/math] и [math] Y [/math] соответственно, имеющих в [math] G [/math] степень [math] n ~ (n = 1, ~ 2, ~ 3, ~ \ldots) [/math]. Тогда: [math] \sum\limits_{n=1}^{\infty} (n - 2) (f_n^{X} - f_n^{Y}) = 0 ~~~ \bf{(1)} [/math].

Доказательство:

[math]\triangleright[/math]

Так как торцевые графы являются деревьями, то количество их вершин на единицу больше количества ребер: [math] \sum\limits_{n=1}^{\infty} f_n^{X} = |V(X)| = |E(X)| + 1 ~~~ \textbf{(2)} [/math]. Посчитаем [math] \sum\limits_{n=1}^{\infty} n f_n^{X} [/math], то есть количество всех исходящих ребер из [math]X[/math]. По лемме о рукопожатиях внутри [math]X[/math] их будет [math]2|E(X)|[/math], но мы не посчитали ребра прикрепленные и к [math]X[/math], и к [math]Y[/math]. Количество таких ребер, по определению бонда — количество ребер в бонде [math]H[/math], то есть [math]|E(H)|[/math]. Отсюда: [math] \sum\limits_{n=1}^{\infty} n f_n^{X} = |E(H)| + 2|E(X)| ~~~ \textbf{(3)} [/math]. Поэтому: [math] \textbf{(2)} - 2 \times \textbf{(3)} = \sum\limits_{n=1}^{\infty} (n - 2) f_n^{X} = |E(H)| - 2 ~~~ \textbf{(4)} [/math]. Аналогичную формулу получаем для графа [math] Y [/math]. Вычитая ее из [math]\textbf{(4)}[/math], приходим к [math]\textbf{(1)}[/math].

[math]\triangleleft[/math]

Использование теоремы

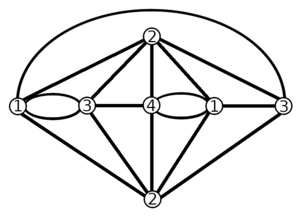
Теорему Гринберга можно иногда использовать для доказательства отсутствия гамильтонова бонда в графе. Пусть, например, все вершины связного графа [math] G [/math], кроме одной, имеют степени, сравнимые с 2 по модулю 3. Тогда левая часть формулы (1) не делится на 3 и, следовательно, гамильтонова бонда в графе [math] G [/math] не существует. Рисунок 1 иллюстрирует этот простой пример.

Рис. 1

См. также

• Гамильтоновы графы

Источники информации

• У. Татт. Теория графов. М.: "Мир", 1988. с. 304. ISBN 5-03-001001-7