Квантовые алгоритмы — различия между версиями
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition='''Квантовый алгоритм''' (англ. ''quantum algorithm'') представляет собой классический алгоритм, который задает последовательность унитарных операций ([[Квантовые гейты|гейтов]] | + | |definition='''Квантовый алгоритм''' (англ. ''quantum algorithm'') представляет собой классический алгоритм, который задает последовательность унитарных операций ([[Квантовые гейты|гейтов]], или вентилей) с указанием, над какими именно кубитами<ref>[https://ru.wikipedia.org/wiki/%D0%9A%D1%83%D0%B1%D0%B8%D1%82 Википедия {{---}} Кубит]</ref> их надо совершать. |
}} | }} | ||
| Строка 6: | Строка 6: | ||
=== Постановка задачи === | === Постановка задачи === | ||
{{Задача | {{Задача | ||
| − | |definition=Пусть имеется функция <tex> f: A \rightarrow B </tex>, такая, что <tex>f(x)=xu | + | |definition=Пусть имеется функция <tex> f: A \rightarrow B </tex>, такая, что <tex>f(x)=xu\bmod 2</tex> с неизвестным <tex>u</tex>. Найти <tex>u</tex> за минимальное количество обращений к функции <tex>f</tex>. |
}} | }} | ||
'''Пример:''' | '''Пример:''' | ||
| Строка 37: | Строка 37: | ||
<tex>\mid -\bigr\rangle = \dfrac{1}{\sqrt{2}}(\mid 0\bigr\rangle - \mid 1\bigr\rangle)</tex> | <tex>\mid -\bigr\rangle = \dfrac{1}{\sqrt{2}}(\mid 0\bigr\rangle - \mid 1\bigr\rangle)</tex> | ||
| − | Выразим неизвестную: <tex>\mid 00 | + | Выразим неизвестную: <tex>\mid 00\ldots0\bigr\rangle\mid -\bigr\rangle\rightarrow\dfrac{1}{2^{n/2}} \Leftrightarrow \sum_\limits{x \mathop \in \{0,1\}^n} \mid x\bigr\rangle\mid-\bigr\rangle\rightarrow\dfrac{1}{2^{n/2}} \Leftrightarrow \sum_\limits{x \mathop \in \{0,1\}^n} (-1)^{xu}\mid x\bigr\rangle\mid-\bigr\rangle\rightarrow\mid u\bigr\rangle\mid-\bigr\rangle</tex> |
=== Сложность === | === Сложность === | ||
| Строка 98: | Строка 98: | ||
=== Постановка задачи === | === Постановка задачи === | ||
{{Задача | {{Задача | ||
| − | |definition=Пусть имеется функция <tex> f: \{0, | + | |definition=Пусть имеется функция <tex> f: \{0,\ldots,N-1\} \rightarrow S </tex>, такая, что <tex>f(x+r\bmod N)=f(x)</tex> с неизвестным периодом <tex>r</tex>. Найти <tex>r</tex> за минимальное количество обращений к функции <tex>f</tex>. |
}} | }} | ||
| Строка 104: | Строка 104: | ||
[[Файл:Quantumalgorithm.QFT.png|470px|thumb|right|]] | [[Файл:Quantumalgorithm.QFT.png|470px|thumb|right|]] | ||
=== Реализация === | === Реализация === | ||
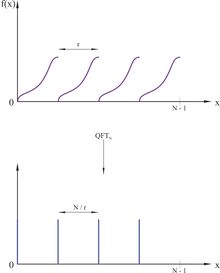
| − | [[Файл:Quantum algorithm. QFT. Graph3.jpg|220px|thumb|left|<tex>r</tex> и <tex>N/r</tex> - периоды функций]] | + | [[Файл:Quantum algorithm. QFT. Graph3.jpg|220px|thumb|left|<tex>r</tex> и <tex>N/r</tex> {{---}} периоды функций]] |
| − | Чтобы решить задачу, воспользуемся квантовым преобразованием Фурье<ref>[https://en.wikipedia.org/wiki/Quantum_Fourier_transform Wikipedia {{---}} Quantum Fourier transform]</ref>(англ. ''Quantum Fourier transform''; далее '''''QFT'''''). '''''QFT''''' - гейт, который реализует матрицу дискретного преобразования Фурье<ref>[https://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5 Википедия {{---}} Дискретное преобразование Фурье]</ref> над квантовым состоянием. Идея в следующем: есть периодическая функция с периодом <tex>r</tex>, после '''''QFT''''', получим новую периодическую функцию с периодом <tex>N/r</tex>, где <tex>N</tex> - модуль, с которым мы работаем. | + | Чтобы решить задачу, воспользуемся квантовым преобразованием Фурье<ref>[https://en.wikipedia.org/wiki/Quantum_Fourier_transform Wikipedia {{---}} Quantum Fourier transform]</ref>(англ. ''Quantum Fourier transform''; далее '''''QFT'''''). '''''QFT''''' {{---}} гейт, который реализует матрицу дискретного преобразования Фурье<ref>[https://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%A4%D1%83%D1%80%D1%8C%D0%B5 Википедия {{---}} Дискретное преобразование Фурье]</ref> над квантовым состоянием. Идея в следующем: есть периодическая функция с периодом <tex>r</tex>, после '''''QFT''''', получим новую периодическую функцию с периодом <tex>N/r</tex>, где <tex>N</tex> {{---}} модуль, с которым мы работаем. |
<tex> QFT_N = \dfrac{1}{\sqrt{N}}\begin{vmatrix} 1 & 1 & 1 & \cdots & 1 | <tex> QFT_N = \dfrac{1}{\sqrt{N}}\begin{vmatrix} 1 & 1 & 1 & \cdots & 1 | ||
Версия 21:52, 30 октября 2018
| Определение: |
| Квантовый алгоритм (англ. quantum algorithm) представляет собой классический алгоритм, который задает последовательность унитарных операций (гейтов, или вентилей) с указанием, над какими именно кубитами[1] их надо совершать. |
Содержание
Алгоритм проверки чётности
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным . Найти за минимальное количество обращений к функции . |
Пример:
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
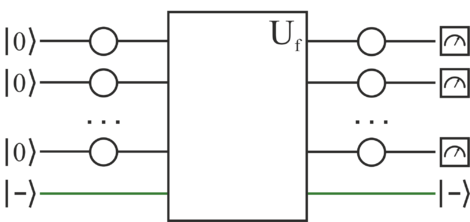
Реализация
Для начала инициализируем начальные кубитов состоянием ноль. Проводим их всех через гейт Адамара (англ. Hadamard gate) и получаем все возможные суперпозиции. Суперпозиции передаём в "черный ящик", который реализован в виде вентиля . Сам результат опять пропускаем через гейт Адамара. В конце измеряем результат, который будет являться искомой .
В качестве бита, который будет содержать ответ, будет использоваться суперпозиция:
Выразим неизвестную:
Сложность
Классический алгоритм: .
Квантовый алгоритм: . Такая сложность достигается благодаря квантовым свойства[2], а конкретно параллелизму[3].
Алгоритм Саймона
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным . Найти за минимальное количество обращений к функции . |
Пример:
| 000 | 010 | 001 | 100 | 010 | 000 | 100 | 001 |
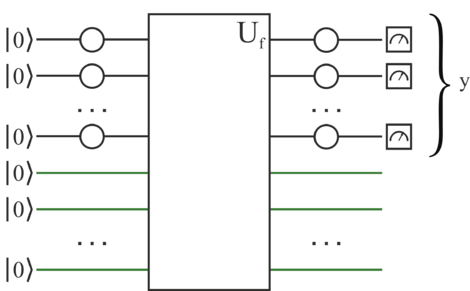
Реализация
Задача похожа на задачу нахождения коллизии, так как необходимо найти два значения, при которых их выходные значения будет одинаковыми, затем вычислить между ними разницу, которая и будет ответом задачи.
Аналогично предыдущему алгоритму вычисляем результат, который будет являться некоторой строкой, дающей при скалярном умножении на искомую ноль. После итерации алгоритма получим систему из линейных уравнений; решив эту систему уравнений, найдём искомую .
Особенности алгоритма:
- для решения СЛАУ [4] необходим препроцессинг на классическом компьютере;
- алгоритм может допускать ошибку(возможно, какие-то уравнения не будут линейно независимыми и система не будет иметь решений) с вероятностью при одном цикле прохода алгоритма. Этого можно избежать, если прогнать алгоритм несколько раз, так для раз, вероятность будет равна: . Например, при вероятность будет .
Сложность
Классический алгоритм: .
Квантовый алгоритм: .
Алгоритм нахождения периода
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным периодом . Найти за минимальное количество обращений к функции . |
Перефразируем задачу: у нас есть периодичная функция, для которой необходимо найти её период, путём нахождения коллизии.
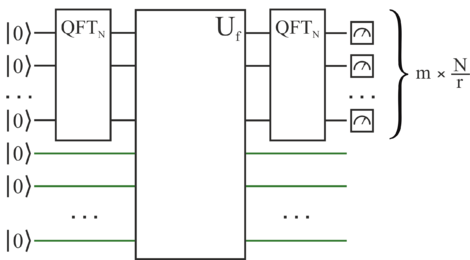
Реализация
Чтобы решить задачу, воспользуемся квантовым преобразованием Фурье[5](англ. Quantum Fourier transform; далее QFT). QFT — гейт, который реализует матрицу дискретного преобразования Фурье[6] над квантовым состоянием. Идея в следующем: есть периодическая функция с периодом , после QFT, получим новую периодическую функцию с периодом , где — модуль, с которым мы работаем.
, где
Так аналогично предыдущему алгоритму, но пользуясь QFT, получаем результат . Выполнив данный алгоритм раз, найдём наибольший общий делитель[7] от полученных чисел, который, с некоторой вероятностью, будет искомым периодом , при этом вероятность ошибки будет экспоненциально падать с каждой попыткой.
Примечание: Алгоритм нахождения периода используется в алгоритме Шора[8], который позволяет решать задачу факторизации числа.
Сложность
Классический алгоритм: .
Квантовый алгоритм: .
См.также
- Квантовые гейты
- Алгоритм Гровера
- Алгоритм Шора
- Веб-приложение, использующее WebGL, чтобы имитировать до 22 кубитов на GPU
- Веб-приложение, для написания и визуализации квантовых алгоритмов
- Языки программирования для квантового компьютера
Примечания
- ↑ Википедия — Кубит
- ↑ Википедия — Квантовый компьютер
- ↑ Википедия — Квантовый параллелизм
- ↑ Википедия — Система линейных алгебраических уравнений
- ↑ Wikipedia — Quantum Fourier transform
- ↑ Википедия — Дискретное преобразование Фурье
- ↑ Википедия — Наибольший общий делитель
- ↑ Wikipedia — Shor's algorithm