Проблема четырёх красок — различия между версиями
Mervap (обсуждение | вклад) (Новая страница: «{{Теорема |about= Проблема четырех красок |statement='''Теорема о четырёх красках''' — утверждение…») |
Mervap (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| + | == Краткая история == | ||
| + | Раскрашивая географическую карту естественно пользоваться по возможности меньшим количеством цветов, однако так, чтобы две страны, имеющие общую часть границы (не только общую точку), были окрашены по-разному. В 1852 году Френсис Гутри, составляя карту графств Англии, обратил внимание, что для такой цели вполне хватает четырех красок. Его брат, Фредерик, сообщил об этом наблюдении известному математику О. Де Моргану, а тот – математической общественности. Точная формулировка гипотезы опубликована А. Кэли в 1878 году. Первое доказательство появилось год спустя и принадлежало В. Кемпе. Одиннадцать лет спустя П. Хивуд обнаружил в нем ошибку. (Однако из доказательства Хивуд понял, что пяти красок действительно достаточно). За первым ошибочным доказательством последовало множество других. До середины XX века, хотя проблемой четырех красок занимались многие выдающиеся математики, положение с доказательством изменилось несущественно: идеи Дж. Д. Биркгофа позволили П. Франклину в 1913 году доказать гипотезу для карты с не более чем 25 странами. Позже это число было увеличено до 38. В 1977 году доказательство гипотезы четырех красок было наконец получено К. Аппелем и У. Хакеном и опубликовано в двух статьях. Значительную часть рутинных проверок выполнил компьютер, и это революционное нововведение в сложившуюся практику дедуктивных рассуждений в чистой математике служит основанием для некоторого естественного скептицизма по отношению к данному доказательству и по сей день. | ||
| + | |||
| + | |||
| + | == Формулировка проблемы == | ||
{{Теорема | {{Теорема | ||
|about= | |about= | ||
| Строка 4: | Строка 9: | ||
|statement='''Теорема о четырёх красках''' — утверждение о том, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. | |statement='''Теорема о четырёх красках''' — утверждение о том, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. | ||
}} | }} | ||
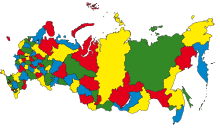
| − | [[Файл:Map of Russia(four colour).png|230px|thumb|right| | + | [[Файл:Map of Russia(four colour).png|230px|thumb|right|Карта России раскрашенная в <tex>4</tex> цвета]] |
| + | |||
| + | Начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. Выберем столицу у каждой страны (то есть выберем по одной внутренней точке в каждой из стран) и соединим дугами столицы стран, имеющих общий сегмент границы. В результате получится [[Укладка графа на плоскости|планарный граф]]. Тогда следующая теорема эквивалентна теореме выше: | ||
| + | {{Теорема | ||
| + | |about= | ||
| + | Хроматическое число планарного графа | ||
| + | |statement= [[Раскраска_графа#chromatic_number_difinition|Хроматическое число]] планарного графа не превосходит 4. | ||
| + | }} | ||
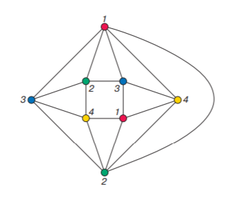
| + | [[Файл:Раскраска_планарного_графа_в_4_цвета.png|230px|thumb|right|4-раскраска планарного графа]] | ||
Версия 03:21, 10 ноября 2018
Краткая история
Раскрашивая географическую карту естественно пользоваться по возможности меньшим количеством цветов, однако так, чтобы две страны, имеющие общую часть границы (не только общую точку), были окрашены по-разному. В 1852 году Френсис Гутри, составляя карту графств Англии, обратил внимание, что для такой цели вполне хватает четырех красок. Его брат, Фредерик, сообщил об этом наблюдении известному математику О. Де Моргану, а тот – математической общественности. Точная формулировка гипотезы опубликована А. Кэли в 1878 году. Первое доказательство появилось год спустя и принадлежало В. Кемпе. Одиннадцать лет спустя П. Хивуд обнаружил в нем ошибку. (Однако из доказательства Хивуд понял, что пяти красок действительно достаточно). За первым ошибочным доказательством последовало множество других. До середины XX века, хотя проблемой четырех красок занимались многие выдающиеся математики, положение с доказательством изменилось несущественно: идеи Дж. Д. Биркгофа позволили П. Франклину в 1913 году доказать гипотезу для карты с не более чем 25 странами. Позже это число было увеличено до 38. В 1977 году доказательство гипотезы четырех красок было наконец получено К. Аппелем и У. Хакеном и опубликовано в двух статьях. Значительную часть рутинных проверок выполнил компьютер, и это революционное нововведение в сложившуюся практику дедуктивных рассуждений в чистой математике служит основанием для некоторого естественного скептицизма по отношению к данному доказательству и по сей день.
Формулировка проблемы
| Теорема (Проблема четырех красок): |
Теорема о четырёх красках — утверждение о том, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. |
Начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. Выберем столицу у каждой страны (то есть выберем по одной внутренней точке в каждой из стран) и соединим дугами столицы стран, имеющих общий сегмент границы. В результате получится планарный граф. Тогда следующая теорема эквивалентна теореме выше:
| Теорема (Хроматическое число планарного графа): |
Хроматическое число планарного графа не превосходит 4. |