Мультиплексор и демультиплексор

Эта статья находится в разработке!

Определение:

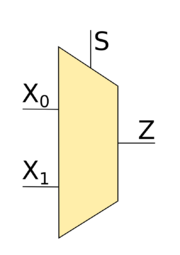
Мультиплексор (англ. multiplexer, или mux) — логическая схема, имеющая [math]2^n + n[/math] входов [math]x_0[/math], [math]x_1[/math], [math]\ldots[/math], [math]x_{2^n-1}[/math], [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math] и один выход [math]z[/math], на который подаётся значение на входе [math]x_i[/math], где [math]i[/math] — число, которое кодируется входами [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math].

Определение:

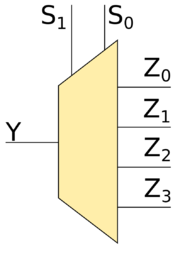
Демультиплексор (англ. demultiplexer, или demux) — логическая схема, имеющая [math]n+1[/math] входов [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math], [math]x[/math] и [math]2^n[/math] выходов [math]z_0[/math], [math]z_1[/math], [math]\ldots[/math], [math]z_{2^n-1}[/math]. На все выходы подаётся [math]0[/math] кроме выхода [math]z_i[/math], на который подаётся значение на входе [math]y[/math], где [math]i[/math] — число, которое кодируется входами [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math].

Принцип работы мультиплексора

[math]2[/math]—to—[math]1[/math] мультиплексор

[math]4[/math]—to—[math]1[/math] мультиплексор

Мультиплексор 2-to-1

Рассмотрим мультиплексор [math]2[/math]-to-[math]1[/math] (это значит, что есть всего два входа [math]x_0[/math] и [math]x_1[/math], значения которых могут подаваться на вход [math]z[/math]). Переберём всевозможные варианты значений на входах. Если на [math]s[/math] подавать [math]0[/math], то на выход [math]z[/math] будет подаваться то же значение, которое подаётся на вход [math]x_0[/math], т.е. в данном случае значение на входе [math]x_1[/math] нас не интересует. Аналогично, если на вход [math]s[/math] подавать [math]1[/math], то на выход [math]z[/math] будет подаваться то же значение, которое подаётся на вход [math]x_1[/math]. Для более лучшего понимания посмотрим на таблицу истинности.

[math]s[/math]	[math]x_0[/math]	[math]x_1[/math]	[math]z[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]

Мультиплексор 4-to-1

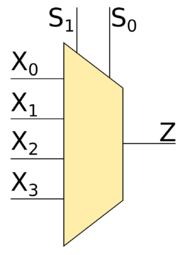
Также рассмотрим мультиплексор [math]4[/math]-to-[math]1[/math] (это значит, что есть четыре входа [math]x_0[/math], [math]x_1[/math], [math]x_2[/math] и [math]x_3[/math], значения которых могут подаваться на выход [math]z[/math]). Также переберём всевозможные варианты значений на входах. Тут уже [math]2[/math] входа [math]s_0[/math] и [math]s_1[/math], которые определяют, значение какого из входов [math]x_0[/math], [math]x_1[/math], [math]x_2[/math] или [math]x_3[/math] будет подаваться на выход [math]z[/math]. Если [math]s_0 = s_1 = 0[/math], то на выход [math]z[/math] будет подаваться значение входа [math]x_0[/math], если [math]s_0 = 1[/math] и [math]s_1 = 0[/math] — то значение [math]x_1[/math], если [math]s_0 = 0[/math] и [math]s_1 = 1[/math] — то значение [math]x_2[/math], в противном случае — значение [math]x_3[/math]. Для более лучшее понимания рекомендуется обратиться к таблице истинности.

[math]s_0[/math]	[math]s_1[/math]	[math]x_0[/math]	[math]x_1[/math]	[math]x_2[/math]	[math]x_3[/math]	[math]z[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]

Логическая схема мультиплексора

Заметим, что дешифратор имеет [math]n[/math] входов и [math]2^n[/math] выходов, причём на все выходы дешифратора подаётся [math]0[/math] кроме выхода [math]z_i[/math], на который подаётся [math]1[/math], где [math]i[/math] — число, которое кодируется его входами.

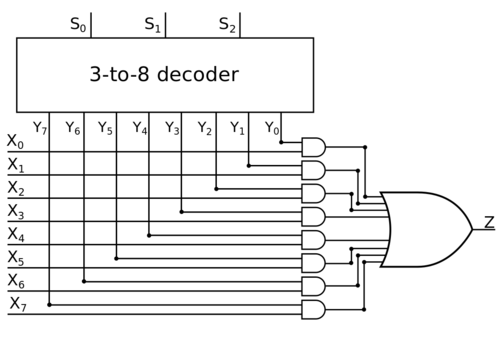
Тогда давайте построим дешифратор [math]n[/math]-to-[math]2^n[/math] (это значит, что у дешифратора имеется [math]n[/math] входов и [math]2^n[/math] выходов), на вход ему подадим входы [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math], а выходы этого дешифратора обозначим как [math]y_0[/math], [math]y_1[/math], [math]\ldots[/math], [math]y_{2^n-1}[/math], а потом с помощью гейта [math]AND[/math] соединим выход [math]y_i[/math] дешифратора с входом [math]x_i[/math] мультиплексора, потом соединим все гейты с выходом [math]z[/math]. Давайте разберёмся, почему эта схема правильная: очевидно, что если входы [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math] [math]s_{n-1}[/math] кодируют вход [math]i[/math], то это значит, что только [math]y_i[/math] выход дешифратора будет иметь [math]1[/math], тогда как на остальных выходах будет [math]0[/math], значит, что значения на входах [math]x_0[/math], [math]x_1[/math], [math]\ldots[/math], [math]x_{i-1}[/math], [math]x_{i+1}[/math], [math]\ldots[/math], [math]x_{2^n-1}[/math] на ответ никак повлиять не могут. Теперь, если на входе [math]x_i[/math] было [math]0[/math], то на выходе [math]z[/math] будет [math]0[/math], если же на входе [math]x_i[/math] был [math]1[/math], то на выходе [math]z[/math] будет [math]1[/math].

Логическая схема мультиплексора [math]8[/math]-to-[math]1[/math]

Принцип работы демультиплексора

[math]1[/math]-to-[math]2[/math] демультиплексор

[math]1[/math]-to-[math]4[/math] демультиплексор

Демультиплексор 1-to-2

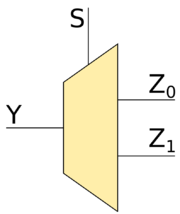
Рассмотрим демультиплексор [math]1[/math]-to-[math]2[/math] (это значит, что у демультиплексора два выхода). Если на вход [math]s[/math] подать значение [math]0[/math], то на выход [math]z_0[/math] будет подаваться то же значение, которое подаётся на вход [math]y[/math], а на выход [math]z_1[/math] будет подаваться [math]0[/math]. Если же на вход [math]s[/math] подать значение [math]1[/math], то на выход [math]z_0[/math] будет подаваться значение [math]0[/math], а на выход [math]z_1[/math] то же значение, которое будет подаваться на вход [math]y[/math]. Для более лучшего понимания посмотрим на таблицу истинности.

[math]s[/math]	[math]y[/math]	[math]z_0[/math]	[math]z_1[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]\textbf{1}[/math]

Демультиплексор 1-to-4

Также рассмотрим демультиплексор [math]1[/math]-to-[math]4[/math] (это значит, что у демультиплексора четыре выхода). Теперь у нас уже есть два входа [math]s_0[/math] и [math]s_1[/math], которые определяют, на какой из выходов [math]z_0[/math], [math]z_1[/math], [math]z_2[/math] или [math]z_3[/math] будет подаваться значение [math]y[/math], тогда как на остальные выходы будет подаваться [math]0[/math]. В случае, когда [math]s_0 = s_1 = 0[/math], то на выход [math]z_0[/math] будет подаваться значение на входе [math]y[/math], тогда как на [math]z_1[/math], [math]z_2[/math] и [math]z_3[/math] будет подаваться [math]0[/math]. Если же [math]s_0 = 1[/math] и [math]s_1 = 0[/math], то на выходы [math]z_0[/math], [math]z_2[/math] и [math]z_3[/math] будет подаваться [math]0[/math], а на выход [math]z_1[/math] будет подаваться то же, что подаётся на вход [math]y[/math]. Аналогично разбираются случаи [math]s_0 = 0[/math], [math]s_1 = 1[/math] и [math]s_0 = s_1 = 1[/math]. Для более лучшего понимания посмотрим на таблицу истинности.

[math]s_0[/math]	[math]s_1[/math]	[math]y[/math]	[math]z_0[/math]	[math]z_1[/math]	[math]z_2[/math]	[math]z_3[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{0}[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{1}[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{1}[/math]

Логическая схема демультиплексора

Построим схему, аналогичную схеме мультиплексора.

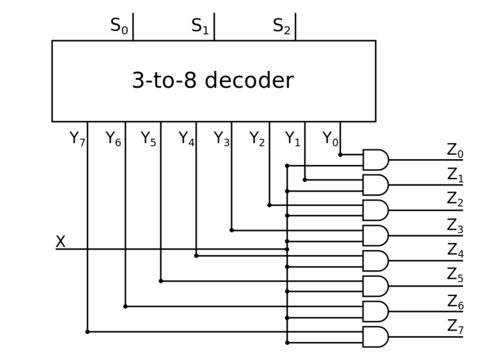
Тогда давайте построим дешифратор, [math]n[/math]-to-[math]2^n[/math], на входы дешифратора подадим входы [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math], а выходы этого дешифратора мы обозначим как [math]y_0[/math], [math]y_1[/math], [math]\ldots[/math], [math]y_{2^n-1}[/math]. Поставим [math]2^n[/math] гейтов [math]AND[/math] и соединим каждый из выходов дешифратора [math]y_0[/math], [math]y_1[/math], [math]\ldots[/math], [math]y_{2^n-1}[/math] со входом [math]x[/math] с помощью гейта [math]AND[/math], потом соединим соответственные гейты с выходами [math]z_0[/math], [math]z_1[/math], [math]\ldots[/math], [math]z_{2^n-1}[/math], причем мы соединим гейт [math]AND[/math] с выходом [math]z_i[/math], если на этот гейт приходится выход дешифратора [math]y_i[/math].

Логическая схема демультиплексора [math]1[/math]-to-[math]8[/math]

Применение мультиплексора и демультиплексора в реальной жизни

Мультиплексоры и демультиплексоры часто используются в электронных схемах. Один из типов мультиплексоров и демультиплексоров используется для разделения на временные слоты и предоставления каждому объекту логической цепи свой временной промежуток, когда можно обмениваться данными с другими объектами с использованием минимального количества проводов. В качестве примера можно привести телефонные станции, которые соединяются с помощью одного провода, а для обеспечения помехоустойчивой связи используются временные слоты, в которые только одна из станций может обмениваться данными с остальными.

Также мультиплексоры и демультиплексоры используются в современных мобильных телефонах для того, чтобы воспроизводить звук и видео с помощью минимального количества проводников, а именно можно использую всего 24 провода

Модуль памяти

Также с помощью мультиплексоров и демультиплексоров можно построить логику некоторых компонентов компьютера, в том числе и можно построить схему модуля памяти с использованием мультиплексора и демультиплексора.

В качестве примера рассмотрим модуль памяти на 8 бит. Для того, чтобы модуль памяти мог обрабатывать запросы, есть управляющие входы [math]A_0[/math], [math]A_1[/math], [math]A_2[/math], которые кодируют номер бита, к которому делается запрос. Существует два типа запросов:

• Прочитать значение, записанное в [math]i[/math]-ом бите. В этом случае на вход [math]R/W[/math] подаётся [math]0[/math].
• Записать в [math]i[/math]-ый бит значение на входе [math]D[/math]. В этом случае на вход [math]R/W[/math] подаётся [math]1[/math].

Также для корректной работы модуля памяти используется провод синхронизации [math]C[/math].

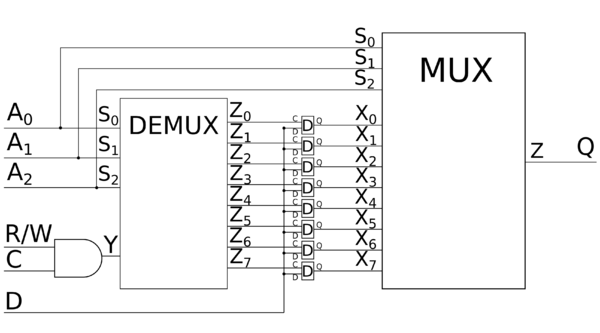
На рисунке представлена схема такой памяти. Для хранения значений в битах используются [math]D[/math]-триггеры. Рассмотрим схему подробнее. Если на входе [math]C[/math] записано значение [math]0[/math], то нам не важно, что находится на выходе [math]Q[/math], поэтому эту ситуацию можно свести к ситуации, когда на [math]C[/math] подано [math]1[/math], а на [math]R/W[/math] - [math]0[/math]. Поймём, как реализованы операции чтения и записи. Существует демультиплексор [math]3[/math]-to-[math]8[/math], которому на вход [math]Y[/math] подадим результат конъюнкции входов [math]R/W[/math] и [math]C[/math], а на входы [math]S_0[/math], [math]S_1[/math], [math]S_2[/math] подадим значения на входах [math]A_0[/math], [math]A_1[/math], [math]A_2[/math]. Пусть число [math]i[/math] кодируется входами [math]A_0[/math], [math]A_1[/math], [math]A_2[/math]. Тогда на все выходы демультиплексора, кроме выхода [math]Z_i[/math] будет подаваться [math]0[/math], а на выход [math]Z_i[/math] - значение на входе [math]Y[/math]. Очевидно, что операция чтения никак не изменяет значение битов, в то время как запись меняет их значения, поэтому можно считать, что модуль памяти всегда возвращает значение на [math]i[/math]-ом бите, кроме случаев, когда [math]C = R/W = 1[/math]. Подадим все выходы демультиплексора на соответствующие им входы [math]C[/math] [math]D[/math]-триггеров. Оставшиеся свободными входы триггеров соединим со входом [math]D[/math] модуля памяти. Тогда все триггеры, возможно, кроме [math]i[/math]-го триггера будут только возвращать значения, записанные в них, и только [math]i[/math]-ый триггер поменяет своё значение в случае, если [math]C = R/W = 1[/math]. Также есть мультиплексор [math]8[/math]-to-[math]1[/math], которому на входы [math]X_0[/math], [math]X_1[/math], [math]\ldots[/math], [math]X_7[/math] подают значения соответственных триггеров, а на входы [math]S_0[/math], [math]S_1[/math], [math]S_2[/math] подают значения на входах [math]A_0[/math], [math]A_1[/math], [math]A_2[/math]. Тогда мультиплексор всегда возвращает значение, хранящееся в [math]i[/math]-ом бите. Очевидно, что на любой запрос чтения значения в [math]i[/math]-ом бите модуль памяти возвращает то, что нужно, а что схема возвращает на запрос записи неважно.

Однако, такая схема редко используется в реальных электронно-вычислительных машинах, поскольку иногда требуется делать несколько миллионов ячеек памяти, а с помощью такого модуля памяти сделать это будет очень трудно, поскольку такая схема будет потреблять большое количество энергии, а также требует много места и большого количества проводников, что влияет на качество передачи сигнала по проводам. Гораздо эффективнее использовать матричную память, поскольку она позволяет с использованием меньшее количества проводов управлять большим количеством ячеек, а также она менее громоздкая.

Логическая схема модуля памяти на 8 бит

См. также

• Реализация булевой функции схемой из функциональных элементов
• Метод Лупанова синтеза схем
• Дешифратор

Источники информации

• Wikipedia - Multiplexer