Контекстное моделирование — различия между версиями
SchrodZzz (обсуждение | вклад) (Новая страница: «{{Определение |definition= '''''Контекстное моделирование''''' — ''оценка вероятности появления с…») (Метки: правка с мобильного устройства, правка из мобильной версии) |
SchrodZzz (обсуждение | вклад) (Метки: правка с мобильного устройства, правка из мобильной версии) |
||
| Строка 98: | Строка 98: | ||
==Метод PPM== | ==Метод PPM== | ||
===Описание=== | ===Описание=== | ||
| − | <tex>РРМ</tex> относится к ''адаптивным'' методам моделирования. Исходно кодеру и декодеру поставлена в соответствие ''начальная'' модель источника данных. Будем считать, что она состоит из <tex>КМ(-1)</tex>, присваивающей одинаковую вероятность всем символам алфавита входной последовательности. После обработки текущего символа кодер и декодер изменяют свои модели одинаковым образом, в частности ''наращивая'' величину оценки вероятности рассматриваемого символа. Следующий символ кодируется (декодируется) на основании новой, измененной модели, после чего модель снова модифицируется и т. д. На каждом шаге обеспечивается ''идентичность'' модели кодера и декодера за счет применения одинакового механизма ее обновления. | + | <tex>РРМ</tex> (''Prediction by partial matching'') относится к ''адаптивным'' методам моделирования. Исходно кодеру и декодеру поставлена в соответствие ''начальная'' модель источника данных. Будем считать, что она состоит из <tex>КМ(-1)</tex>, присваивающей одинаковую вероятность всем символам алфавита входной последовательности. После обработки текущего символа кодер и декодер изменяют свои модели одинаковым образом, в частности ''наращивая'' величину оценки вероятности рассматриваемого символа. Следующий символ кодируется (декодируется) на основании новой, измененной модели, после чего модель снова модифицируется и т. д. На каждом шаге обеспечивается ''идентичность'' модели кодера и декодера за счет применения одинакового механизма ее обновления. |
===Пример=== | ===Пример=== | ||
| + | ====Кодирование==== | ||
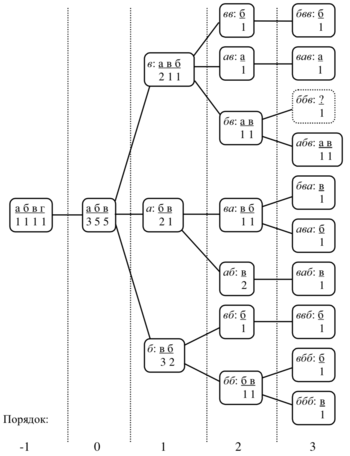
Имеется последовательность символов <tex>“абвавабввбббв”</tex> алфавита <tex> \{“а”, “б”, “в”, “г”\}</tex>, которая уже была ''закодирована''. | Имеется последовательность символов <tex>“абвавабввбббв”</tex> алфавита <tex> \{“а”, “б”, “в”, “г”\}</tex>, которая уже была ''закодирована''. | ||
[[Файл: Qq.png|350px|thumb|right|рис. 2]] | [[Файл: Qq.png|350px|thumb|right|рис. 2]] | ||
| Строка 154: | Строка 155: | ||
Сначала рассматривается контекст <tex>3</tex>-го порядка <tex>“ббв”</tex>. Ранее он не встречался, поэтому кодер, ничего не послав на выход, переходит к анализу статистики для контекста <tex>2</tex>-го порядка. В этом контексте (<tex>“бв”</tex>) встречались символ <tex>а</tex> и символ <tex>в</tex>, счетчики которых в соответствующей <tex>КМ</tex> равны <tex>1</tex> каждый, поэтому ''символ ухода'' кодируется с вероятностью <tex>\dfrac{1}{2+1}</tex>, где в знаменателе число <tex>2</tex> — наблюдавшаяся частота появления контекста <tex>“бв”</tex>, <tex>1</tex> — значение счетчика ''символа ухода''. В контексте <tex>1</tex>-го порядка <tex>в</tex> дважды встречался символ <tex>а</tex>, который исключается (маскируется), один раз также исключаемый <tex>в</tex> и один раз <tex>б</tex>, поэтому оценка вероятности ухода будет ''равна'' <tex>\dfrac{1}{1+1}</tex>. В <tex>КМ(0)</tex> символ <tex>г</tex> также оценить ''нельзя'', причем все имеющиеся в этой <tex>КМ</tex> символы <tex>а</tex>, <tex>б</tex>, <tex>в</tex> исключаются, так как уже встречались нам в <tex>КМ</tex> более высокого порядка. Поэтому вероятность ухода получается равной ''единице''. Цикл оценивания завершается на уровне <tex>КМ(-1)</tex>, где <tex>г</tex> к этому времени остается ''единственным'' до сих пор не попавшимся символом, поэтому он получает вероятность <tex>1</tex> и кодируется посредством <tex>0\ бит</tex>. Таким образом, при использовании хорошего статистического кодировщика для представления <tex>г</tex> потребуется в целом примерно <tex>2.6\ бит</tex>. | Сначала рассматривается контекст <tex>3</tex>-го порядка <tex>“ббв”</tex>. Ранее он не встречался, поэтому кодер, ничего не послав на выход, переходит к анализу статистики для контекста <tex>2</tex>-го порядка. В этом контексте (<tex>“бв”</tex>) встречались символ <tex>а</tex> и символ <tex>в</tex>, счетчики которых в соответствующей <tex>КМ</tex> равны <tex>1</tex> каждый, поэтому ''символ ухода'' кодируется с вероятностью <tex>\dfrac{1}{2+1}</tex>, где в знаменателе число <tex>2</tex> — наблюдавшаяся частота появления контекста <tex>“бв”</tex>, <tex>1</tex> — значение счетчика ''символа ухода''. В контексте <tex>1</tex>-го порядка <tex>в</tex> дважды встречался символ <tex>а</tex>, который исключается (маскируется), один раз также исключаемый <tex>в</tex> и один раз <tex>б</tex>, поэтому оценка вероятности ухода будет ''равна'' <tex>\dfrac{1}{1+1}</tex>. В <tex>КМ(0)</tex> символ <tex>г</tex> также оценить ''нельзя'', причем все имеющиеся в этой <tex>КМ</tex> символы <tex>а</tex>, <tex>б</tex>, <tex>в</tex> исключаются, так как уже встречались нам в <tex>КМ</tex> более высокого порядка. Поэтому вероятность ухода получается равной ''единице''. Цикл оценивания завершается на уровне <tex>КМ(-1)</tex>, где <tex>г</tex> к этому времени остается ''единственным'' до сих пор не попавшимся символом, поэтому он получает вероятность <tex>1</tex> и кодируется посредством <tex>0\ бит</tex>. Таким образом, при использовании хорошего статистического кодировщика для представления <tex>г</tex> потребуется в целом примерно <tex>2.6\ бит</tex>. | ||
Перед обработкой следующего символа создается <tex>КМ</tex> для строки <tex>“ббв”</tex> и производится модификация счетчиков символа <tex>г</tex> в созданной и во всех просмотренных <tex>КМ</tex>. В данном случае требуется изменение <tex>КМ</tex> всех порядков от <tex>0</tex> до <tex>N</tex>. | Перед обработкой следующего символа создается <tex>КМ</tex> для строки <tex>“ббв”</tex> и производится модификация счетчиков символа <tex>г</tex> в созданной и во всех просмотренных <tex>КМ</tex>. В данном случае требуется изменение <tex>КМ</tex> всех порядков от <tex>0</tex> до <tex>N</tex>. | ||
| + | ====Декодирование==== | ||
| + | Алгоритм декодирования абсолютно симметричен алгоритму кодирования. После декодирования символа в текущей КМ проверяется, не является ли он символом ухода;, если это так, то выполняется переход к КМ порядком ниже. Иначе считается, что исходный символ восстановлен, он записывается в декодированный поток и осуществляется переход к следующему шагу. Содержание процедур обновления счетчиков, создания новых контекстных моделей, прочих вспомогательных действий и последовательность их применения должны быть строго одинаковыми при кодировании и декодировании. Иначе возможна рассинхронизация копий модели кодера и декодера, что рано или поздно приведет к ошибочному декодированию какого-то символа. Начиная с этой позиции вся оставшаяся часть сжатой последовательности будет разжата неправильно. | ||
| + | Разница между кодами символов, оценки вероятности которых одинаковы, достигается за счет того, что РРМ-предсказатель передает кодировщику так называемые накопленные частоты (или накопленные вероятности) оцениваемого символа и его соседей или кодовые пространства символов. | ||
| + | Так, например, для контекста "бв" из примера 2 можно составить табл. 4.3. | ||
| + | Хороший кодировщик должен отобразить символ 'У с оценкой вероятности q(s) в код длины \og2q{s), что и обеспечит сжатие всей обрабатываемой последовательности в целом. | ||
| + | {| style="background-color:#CCC;margin:0.5px; right" | ||
| + | !style="background-color:#EEE"| <tex>Символ</tex> | ||
| + | !style="background-color:#EEE"| <tex>Частота</tex> | ||
| + | !style="background-color:#EEE"| <tex>Оценка\ вероятности</tex> | ||
| + | !style="background-color:#EEE"| <tex>Накопительная\ оценка</tex> | ||
| + | !style="background-color:#EEE"| <tex>Кодовое пространство</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex>a</tex> | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 1 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> [0 ... 0.33) </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex>б</tex> | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 0 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> — </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex>в</tex> | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 1 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{2}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> [0.33 ... 0.66) </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex>г</tex> | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 0 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> — </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 23px"| <tex>esc</tex> | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 1 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>1</tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> [0.66 ... 1) </tex> | ||
| + | |} | ||
Версия 19:19, 31 декабря 2018
| Определение: |
| Контекстное моделирование — оценка вероятности появления символа (элемента, пиксела, сэмпла и даже набора качественно разных объектов) в зависимости от непосредственно ему предыдущих, или контекста. |
| Определение: |
| Если длина контекста ограничена, то такой подход будем называть контекстным моделированием ограниченного порядка (finite-context modeling), при этом под порядком понимается максимальная длина используемых контекстов . |
Содержание
Оценка вероятности
Оценки вероятностей при контекстном моделировании строятся на основании обычных счетчиков частот, связанных с текущим контекстом. Если мы обработали строку , то для контекста счетчик символа равен двум, символ — единице. На основании этого статистики можно утверждать, что вероятность появления после равна , а вероятность появления равна , т.е. Оценки формируются на основе уже просмотренной части потока.
| Определение: |
| Порядок контекстной модели — длина соответствующего этой модели контекста . Если порядок равен , то будем обозначать такую как |
Пример
Рассмотрим процесс оценки отмеченного на рисунке стрелочкой символа , встречающегося в блоке _
Пусть мы используем контекстное моделирование порядка и делаем полное смешивание оценок распределений вероятностей в второго первого и нулевого порядка с весами , и . Считаем, что в начале кодирования в создаются счетчики для всех символов алфавита и инициализируются единицей; счетчик символа после его обработки увеличивается на единицу. Для текущего символа имеются контексты , и (0-го порядка). К данному моменту для них накоплена статистика, показанная в таблице
| Порядок | _ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Частоты | |||||||||
| Накопленные Частоты | |||||||||
| Частоты | |||||||||
| Накопленные Частоты | |||||||||
| Частоты | |||||||||
| Накопленные Частоты |
Оценка вероятности для символа будет равна
Метод PPM
Описание
(Prediction by partial matching) относится к адаптивным методам моделирования. Исходно кодеру и декодеру поставлена в соответствие начальная модель источника данных. Будем считать, что она состоит из , присваивающей одинаковую вероятность всем символам алфавита входной последовательности. После обработки текущего символа кодер и декодер изменяют свои модели одинаковым образом, в частности наращивая величину оценки вероятности рассматриваемого символа. Следующий символ кодируется (декодируется) на основании новой, измененной модели, после чего модель снова модифицируется и т. д. На каждом шаге обеспечивается идентичность модели кодера и декодера за счет применения одинакового механизма ее обновления.
Пример
Кодирование
Имеется последовательность символов алфавита , которая уже была закодирована.
Пусть счетчик символа ухода равен единице для всех , при обновлении модели счетчики символов увеличиваются на единицу во всех активных , применяется метод исключения и максимальная длина контекста равна трем, т. е. . Первоначально модель состоит из , в которой счетчики всех четырех символов алфавита имеют значение . Состояние модели обработки последовательности представлено на , где прямоугольниками обозначены контекстные модели, при этом для каждой КМ указан курсивом контекст, а также встречавшиеся в контексте символы и их частоты.
Пусть текущий символ равен , т. е. = , тогда процесс его кодирования будет выглядеть следующим образом. Сначала рассматривается контекст -го порядка . Ранее он не встречался, поэтому кодер, ничего не послав на выход, переходит к анализу статистики для контекста -го порядка. В этом контексте () встречались символ и символ , счетчики которых в соответствующей равны каждый, поэтому символ ухода кодируется с вероятностью , где в знаменателе число — наблюдавшаяся частота появления контекста , — значение счетчика символа ухода. В контексте -го порядка дважды встречался символ , который исключается (маскируется), один раз также исключаемый и один раз , поэтому оценка вероятности ухода будет равна . В символ также оценить нельзя, причем все имеющиеся в этой символы , , исключаются, так как уже встречались нам в более высокого порядка. Поэтому вероятность ухода получается равной единице. Цикл оценивания завершается на уровне , где к этому времени остается единственным до сих пор не попавшимся символом, поэтому он получает вероятность и кодируется посредством . Таким образом, при использовании хорошего статистического кодировщика для представления потребуется в целом примерно . Перед обработкой следующего символа создается для строки и производится модификация счетчиков символа в созданной и во всех просмотренных . В данном случае требуется изменение всех порядков от до .
Декодирование
Алгоритм декодирования абсолютно симметричен алгоритму кодирования. После декодирования символа в текущей КМ проверяется, не является ли он символом ухода;, если это так, то выполняется переход к КМ порядком ниже. Иначе считается, что исходный символ восстановлен, он записывается в декодированный поток и осуществляется переход к следующему шагу. Содержание процедур обновления счетчиков, создания новых контекстных моделей, прочих вспомогательных действий и последовательность их применения должны быть строго одинаковыми при кодировании и декодировании. Иначе возможна рассинхронизация копий модели кодера и декодера, что рано или поздно приведет к ошибочному декодированию какого-то символа. Начиная с этой позиции вся оставшаяся часть сжатой последовательности будет разжата неправильно. Разница между кодами символов, оценки вероятности которых одинаковы, достигается за счет того, что РРМ-предсказатель передает кодировщику так называемые накопленные частоты (или накопленные вероятности) оцениваемого символа и его соседей или кодовые пространства символов. Так, например, для контекста "бв" из примера 2 можно составить табл. 4.3. Хороший кодировщик должен отобразить символ 'У с оценкой вероятности q(s) в код длины \og2q{s), что и обеспечит сжатие всей обрабатываемой последовательности в целом.