Дерево решений и случайный лес — различия между версиями
| Строка 29: | Строка 29: | ||
Идея алгоритма <tex>ID3</tex> (англ. ''Induction of Decision Tree'') заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Проще всего записать этот алгоритм в виде рекурсивной процедуры <tex>ID3</tex>, которая строит дерево по заданной подвыборке <tex>U</tex> и возвращает его корневую вершину. | Идея алгоритма <tex>ID3</tex> (англ. ''Induction of Decision Tree'') заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Проще всего записать этот алгоритм в виде рекурсивной процедуры <tex>ID3</tex>, которая строит дерево по заданной подвыборке <tex>U</tex> и возвращает его корневую вершину. | ||
| − | ''' | + | 1:'''function''' ID3(<tex>U</tex>): |
| − | + | 2: '''if''' все объекты множества <tex>U</tex> принадлежат одному классу <tex>y \in Y</tex> | |
| − | + | '''then''' | |
| − | + | 3: создать новый лист <tex>v</tex> | |
| − | + | 4: <tex>y_v = y</tex> | |
| − | + | 5: '''return''' v | |
| − | <tex>\beta= \mathrm{arg}\max_{f\in F} </tex> | + | 6: найти предикат с максимальной информативностью: |
| − | + | <tex>\beta= \mathrm{arg}\max_{f\in F} </tex> I(<tex>f</tex>, <tex>U</tex>) | |
| + | 7: разбить выборку на две части <tex>U = U_0 \cup U_1</tex> по предикату <tex>\beta</tex>: | ||
<tex>U_0 := \{x \in U: f_v(x) = 0\}</tex> | <tex>U_0 := \{x \in U: f_v(x) = 0\}</tex> | ||
<tex>U_1 := \{x \in U: f_v(x) = 1\}</tex> | <tex>U_1 := \{x \in U: f_v(x) = 1\}</tex> | ||
| − | + | 8: '''if''' <tex>U_0 = \emptyset</tex> или <tex>U_1 = \emptyset</tex> | |
'''then''' | '''then''' | ||
| − | + | 9: создать новый лист <tex>v</tex> | |
| − | + | 10: <tex>y_v</tex> = класс, в котором находится большинство объектов из <tex>U</tex> | |
| − | + | 11: '''else''' | |
| − | + | 12: создать новую внутреннюю вершину <tex>v</tex> | |
| − | + | 13: <tex>\beta_v = \beta</tex> | |
| − | + | 14: <tex>S_0</tex> = ID3(<tex>U_0</tex>) | |
| − | + | 15: <tex>S_1</tex> = ID3(<tex>U_1</tex>) | |
| − | + | 16: '''return''' <tex>v</tex> | |
| − | === | + | ===Информативность=== |
===Критерий ветвления=== | ===Критерий ветвления=== | ||
| Строка 57: | Строка 58: | ||
====Энтропийный критерий==== | ====Энтропийный критерий==== | ||
| − | === | + | |
| − | + | == Рецукция решающих деревьев == | |
| − | * | + | Суть редукции состоит в удалении поддеревьев, имеющих недостаточную статистическую надёжность. При этом дерево перестаёт безошибочно классифицировать обучающую выборку, зато качество классификации новых объектов, как правило, улучшается. Рассмотрим наиболее простые варианты редукции. |
| + | |||
| + | ===Предредукция=== | ||
| + | Предредукция (англ. ''pre-pruning'') или критерий раннего останова досрочно прекращает дальнейшее ветвление в вершине дерева, если информативность <tex>I(\beta, U)</tex> для всех возможных предикатов <tex>\beta</tex> не дотягивает до заданного порогового значения <tex>I_0</tex>. <br> | ||
| + | Для этого на шаге 8 алгоритма <tex>ID3</tex> условие <tex>U_0 = \emptyset</tex> или <tex>U_1 = \emptyset</tex> заменяется условием <tex>I(\beta, U) <= I_0 </tex>. Порог <tex>I_0 </tex> является управляющим параметром метода. <br> | ||
| + | Предредукция считается не самым эффективным способом избежать переобучения, так как жадное ветвление по-прежнему остаётся глобально неоптимальным. Более эффективной считается cтратегия постредукции. | ||
| + | |||
| + | ===Постредукция (post-pruning)=== | ||
| + | Постредукция (англ. ''post-pruning'') просматривает все внутренние вершины дерева и заменяет отдельные вершины либо одной из дочерних вершин (при этом вторая дочерняя удаляется), либо терминальной вершиной. Процесс замен продолжается до тех | ||
| + | пор, пока в дереве остаются вершины, удовлетворяющие критерию замены. <br> | ||
| + | ''Критерием замены'' является сокращение числа ошибок на контрольной выборке, отобранной заранее, и не участвовавшей в обучении дерева. Стандартная рекомендация — оставлять в контроле около 30% объектов. <br> | ||
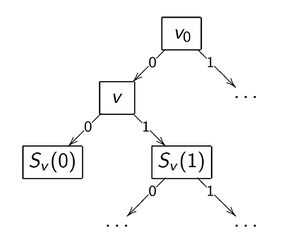
| + | Для реализации постредукции контрольная выборка <tex>X^k</tex> пропускается через | ||
| + | построенное дерево. При этом в каждой внутренней вершине <tex>v</tex> запоминается подмножество <tex>S_v \subseteq X_k</tex> попавших в неё контрольных объектов. Если <tex>S_v = \emptyset </tex>, то вершина <tex>v</tex> считается ненадёжной и заменяется терминальной по ''мажоритарному правилу'': <br> | ||
| + | в качестве <tex>c_v</tex> берётся тот класс, объектов которого больше всего в обучающей подвыборке <tex>U</tex>, пришедшей в вершину <tex>v</tex>. | ||
| + | Затем для каждой внутренней вершины <tex>v</tex> вычисляется число ошибок, полученных при классификации выборки <tex>S_v</tex> следующими способами: <br> | ||
| + | * <tex>r(v)</tex> — классификация поддеревом, растущим из вершины <tex>v</tex>; | ||
| + | * <tex>r_L(v)</tex> — классификация поддеревом левой дочерней вершины <tex>S_v(0)</tex>; | ||
| + | * <tex>r_R(v)</tex> — классификация поддеревом правой дочерней вершины S_v(1); | ||
| + | * <tex>r_c(v)</tex> — отнесение всех объектов выборки <tex>S_v</tex> к классу <tex>y \in Y</tex>. <br> | ||
| + | Эти величины сравниваются, и, в зависимости от того, какая из них оказалась | ||
| + | минимальной, принимается, соответственно, одно из четырёх решений: <br> | ||
| + | * сохранить поддерево вершины <tex>v</tex>; | ||
| + | * заменить поддерево вершины <tex>v</tex> поддеревом левой дочерней вершины Lv; | ||
| + | * заменить поддерево вершины <tex>v</tex> поддеревом правой дочерней вершины Rv; | ||
| + | * заменить поддерево <tex>v</tex> терминальной вершиной класса <tex>y_v = \mathrm{arg}\min_{y\in Y}r_c(v) </tex>. | ||
| + | |||
== Деревья регрессии == | == Деревья регрессии == | ||
| Строка 67: | Строка 93: | ||
* [[Критерий Джини]] | * [[Критерий Джини]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
=== Оценивание вероятностей === | === Оценивание вероятностей === | ||
Версия 20:02, 20 января 2019
Содержание
Дерево решений
| Определение: |
Дерево решений (англ. decision tree, DT) — алгоритм классификации , задающийся деревом (связным ациклическим графом):
|
| Определение: |
Бинарное дерево решений — частный случай дерева решений, для которого .
|
Y classify(x): while : ((x)) ; return
Рекурсивный алгоритм построения бинарного дерева решений ID3
Идея алгоритма (англ. Induction of Decision Tree) заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Проще всего записать этот алгоритм в виде рекурсивной процедуры , которая строит дерево по заданной подвыборке и возвращает его корневую вершину.
1:function ID3(): 2: if все объекты множества принадлежат одному классу then 3: создать новый лист 4: 5: return v 6: найти предикат с максимальной информативностью: I(, ) 7: разбить выборку на две части по предикату : 8: if или then 9: создать новый лист 10: = класс, в котором находится большинство объектов из 11: else 12: создать новую внутреннюю вершину 13: 14: = ID3() 15: = ID3() 16: return
Информативность
Критерий ветвления
Критейрий Джини
Энтропийный критерий
Рецукция решающих деревьев
Суть редукции состоит в удалении поддеревьев, имеющих недостаточную статистическую надёжность. При этом дерево перестаёт безошибочно классифицировать обучающую выборку, зато качество классификации новых объектов, как правило, улучшается. Рассмотрим наиболее простые варианты редукции.
Предредукция
Предредукция (англ. pre-pruning) или критерий раннего останова досрочно прекращает дальнейшее ветвление в вершине дерева, если информативность для всех возможных предикатов не дотягивает до заданного порогового значения .
Для этого на шаге 8 алгоритма условие или заменяется условием . Порог является управляющим параметром метода.
Предредукция считается не самым эффективным способом избежать переобучения, так как жадное ветвление по-прежнему остаётся глобально неоптимальным. Более эффективной считается cтратегия постредукции.
Постредукция (post-pruning)
Постредукция (англ. post-pruning) просматривает все внутренние вершины дерева и заменяет отдельные вершины либо одной из дочерних вершин (при этом вторая дочерняя удаляется), либо терминальной вершиной. Процесс замен продолжается до тех
пор, пока в дереве остаются вершины, удовлетворяющие критерию замены.
Критерием замены является сокращение числа ошибок на контрольной выборке, отобранной заранее, и не участвовавшей в обучении дерева. Стандартная рекомендация — оставлять в контроле около 30% объектов.
Для реализации постредукции контрольная выборка пропускается через
построенное дерево. При этом в каждой внутренней вершине запоминается подмножество попавших в неё контрольных объектов. Если , то вершина считается ненадёжной и заменяется терминальной по мажоритарному правилу:
в качестве берётся тот класс, объектов которого больше всего в обучающей подвыборке , пришедшей в вершину .
Затем для каждой внутренней вершины вычисляется число ошибок, полученных при классификации выборки следующими способами:
- — классификация поддеревом, растущим из вершины ;
- — классификация поддеревом левой дочерней вершины ;
- — классификация поддеревом правой дочерней вершины S_v(1);
- — отнесение всех объектов выборки к классу .
Эти величины сравниваются, и, в зависимости от того, какая из них оказалась
минимальной, принимается, соответственно, одно из четырёх решений:
- сохранить поддерево вершины ;
- заменить поддерево вершины поддеревом левой дочерней вершины Lv;
- заменить поддерево вершины поддеревом правой дочерней вершины Rv;
- заменить поддерево терминальной вершиной класса .
Деревья регрессии
Критерии ветвления
Оценивание вероятностей
Полужадный синтез
Алгоритмы построения решающих деревьев
Обобщающая способность решающих деревьев
Композиции решающих деревьев
- Решающий лес
- Бустинг над решающими деревьями
История
Ссылки
- Classification and Regression Trees — лекции Cosma Shalizi, ноябрь 2009.