Batch-normalization — различия между версиями
(→Обучение нейронных сетей с пакетной нормализацией) |
(→Обучение нейронных сетей с пакетной нормализацией) |
||
| Строка 91: | Строка 91: | ||
{| cellpadding = "20" class = "wikitable" | {| cellpadding = "20" class = "wikitable" | ||
| − | ! Изображение !! Описание | + | ! Шаг !! Изображение !! Описание |
|- | |- | ||
| + | |1 | ||
|[[Файл:step9.png|300px]] | |[[Файл:step9.png|300px]] | ||
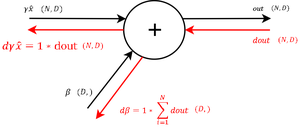
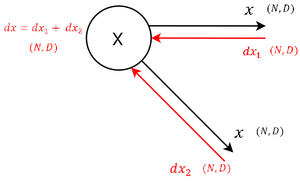
|Сначала вычисляется производная по параметру <tex>\beta</tex>, как в уравнении <tex>(6)</tex>, так как к нему применяется только операции суммирования. И значение градиента выхода передается без изменений. | |Сначала вычисляется производная по параметру <tex>\beta</tex>, как в уравнении <tex>(6)</tex>, так как к нему применяется только операции суммирования. И значение градиента выхода передается без изменений. | ||
|- | |- | ||
| + | |2 | ||
|[[Файл:step8.png|300px]] | |[[Файл:step8.png|300px]] | ||
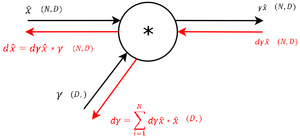
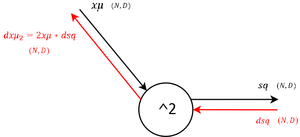
|Далее, пользуясь правилом вычисления производной при умножении, как в уравнении <tex>(5)</tex>, вычисляется градиент по параметру <tex>\gamma</tex>. Градиент выхода умножается на данную константу, получая уравнение <tex>(1)</tex>, и передается в следующий узел. | |Далее, пользуясь правилом вычисления производной при умножении, как в уравнении <tex>(5)</tex>, вычисляется градиент по параметру <tex>\gamma</tex>. Градиент выхода умножается на данную константу, получая уравнение <tex>(1)</tex>, и передается в следующий узел. | ||
|- | |- | ||
| + | |3 | ||
|[[Файл:step7.png|300px]] | |[[Файл:step7.png|300px]] | ||
|Данный шаг вычисляется аналогично предыдущему, применяя правило вычисления производной при умножении. | |Данный шаг вычисляется аналогично предыдущему, применяя правило вычисления производной при умножении. | ||
|- | |- | ||
| + | |4 | ||
|[[Файл:step6.png|300px]] | |[[Файл:step6.png|300px]] | ||
|Пользуясь производной обратной величины, вычисляем следующий узел графа. | |Пользуясь производной обратной величины, вычисляем следующий узел графа. | ||
|- | |- | ||
| + | |5 | ||
|[[Файл:step5.png|300px]] | |[[Файл:step5.png|300px]] | ||
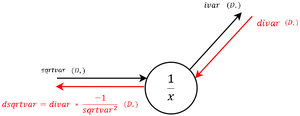
|Вычисляем производную квадратного корня с добавлением <tex>\epsilon</tex>. | |Вычисляем производную квадратного корня с добавлением <tex>\epsilon</tex>. | ||
|- | |- | ||
| + | |6 | ||
|[[Файл:step4.png|300px]] | |[[Файл:step4.png|300px]] | ||
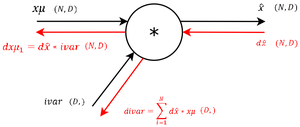
|Вычисляем производную суммы по всем компонентам входного вектора, получая матрицу. | |Вычисляем производную суммы по всем компонентам входного вектора, получая матрицу. | ||
|- | |- | ||
| + | |7 | ||
|[[Файл:step3.png|300px]] | |[[Файл:step3.png|300px]] | ||
|Получаем производную квадрата входящей функции. | |Получаем производную квадрата входящей функции. | ||
|- | |- | ||
| + | |8 | ||
|[[Файл:step2.png|300px]] | |[[Файл:step2.png|300px]] | ||
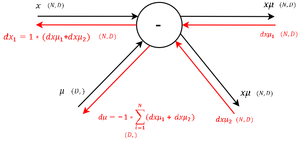
| − | |На данном шаге в одном узле сходятся ветки, поэтому полученные производные просто складываются, получая уравнение <tex>(2)</tex> для дисперсии. | + | |На данном шаге в одном узле сходятся ветки, поэтому полученные производные просто складываются, получая уравнение <tex>(2)</tex> для производной по дисперсии. |
|- | |- | ||
| + | |9 | ||
|[[Файл:step1.png|300px]] | |[[Файл:step1.png|300px]] | ||
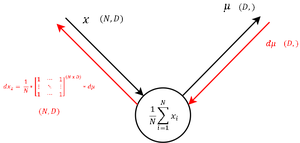
| − | |Аналогично шагу | + | |Аналогично шагу 6 вычисляем матрицу по сумме для производной по математическому ожиданию, получая формулу <tex>(3)</tex>. |
|- | |- | ||
| + | |10 | ||
|[[Файл:step0.png|300px]] | |[[Файл:step0.png|300px]] | ||
|В начальной вершине получаем уравнение <tex>(4)</tex>, складывая входящие производные. | |В начальной вершине получаем уравнение <tex>(4)</tex>, складывая входящие производные. | ||
Версия 19:08, 22 января 2019
Пакетная нормализация (англ. batch-normalization) — это метод, который позволяет повысить производительность и стабилизировать работу искусственных нейронных сетей. Суть данного метода заключается в том, что некоторым слоям нейронной сети на вход подаются данные, предварительно обработанные и имеющие нулевое математическое ожидание и единичную дисперсию. Впервые данный метод был представлен в [1].
Содержание
Идея
Нормализация входного слоя нейронной сети обычно выполняется путем масштабирования данных, подаваемых в функции активации. Например, когда есть признаки со значениями от до и некоторые признаки со значениями от до , то их необходимо нормализовать, чтобы ускорить обучение. Нормализацию данных можно выполнить и в скрытых слоях нейронных сетей, что и делает метод пакетной нормализации.
Пакет
Предварительно, напомним, что такое пакет (англ. batch). Возможны два подхода к реализации алгоритма градиентного спуска для обучения нейросетевых моделей: стохастический и пакетный[2].
- Стохастический градиентный спуск[на 10.01.18 не создано] (англ. stochastic gradient descent) — реализация, в которой на каждой итерации алгоритма из обучающей выборки каким-то (случайным) образом выбирается только один объект.
- Пакетный (батч) (англ. batch gradient descent) — реализация градиентного спуска, когда на каждой итерации обучающая выборка просматривается целиком, и только после этого изменяются веса модели.
Также существует "золотая середина" между стохастическим градиентном спуском и пакетным градиентном спуском — когда просматривается только некоторое подмножество обучающей выборки фиксированного размера (англ. batch-size). В таком случае такие подмножества принято называть мини-пакетом (англ. mini-batch). Здесь и далее, мини-пакеты будем также называть пакетом.
Ковариантный сдвиг

Пакетная нормализация уменьшает величину, на которую смещаются значения узлов в скрытых слоях (т.н. ковариантный сдвиг (англ. covariance shift)).
Ковариантный сдвиг — это ситуация, когда распределения значений признаков в обучающей и тестовой выборке имеют разные параметры (математическое ожидание, дисперсия и т.д.). Ковариантность в данном случае относится к значениям признаков.
Проиллюстрируем ковариантный сдвиг примером. Пусть есть глубокая нейронная сеть, которая обучена определять находится ли на изображении роза. И нейронная сеть была обучена на изображениях только красных роз. Теперь, если попытаться использовать обученную модель для обнаружения роз различных цветов, то, очевидно, точность работы модели будет неудовлетворительной. Это происходит из-за того, что обучающая и тестовая выборки содержат изображения красных роз и роз различных цветов в разных пропорциях. Другими словами, если модель обучена отображению из множества в множество и если пропорция элементов в изменяется, то появляется необходимость обучить модель заново, чтобы "выровнять" пропорции элементов в и . Когда пакеты содержат изображения разных классов, распределенные в одинаковой пропорции на всем множестве, то ковариантный сдвиг незначителен. Однако, когда пакеты выбираются только из одного из двух подмножеств (в данном случае, красные розы и розы различных цветов), то ковариантный сдвиг возрастает. Это довольно сильно замедляет процесс обучения модели. На Рисунке 1 изображена разница в пропорциях.
Простой способ решить проблему ковариантного сдвига для входного слоя — это случайным образом перемешать данные перед созданием пакетов. Но для скрытых слоев нейронной сети такой метод не подходит, так как распределение входных данных для каждого узла скрытых слоев изменяется каждый раз, когда происходит обновление параметров в предыдущем слое. Эта проблема называется внутренним ковариантным сдвигом (англ. internal covariate shift). Для решения данной проблемы часто приходится использовать низкий темп обучения[на 10.01.18 не создано] (англ. learning rate) и методы регуляризации при обучении модели. Другим способом устранения внутреннего ковариантного сдвига является метод пакетной нормализации.
Свойства пакетной нормализации
Кроме того, использование пакетной нормализации обладает еще несколькими дополнительными полезными свойствами:
- достигается более быстрая сходимость моделей, несмотря на выполнение дополнительных вычислений;
- пакетная нормализация позволяет каждому слою сети обучатся более независимо от других слоев;
- становится возможным использование более высокого темпа обучения, так как пакетная нормализация гарантирует, что выходы узлов нейронной сети не будут иметь слишком больших или малых значений;
- пакетная нормализация в каком-то смысле также является механизмом регуляризации: данный метод привносит в выходы узлов скрытых слоев некоторый шум, аналогично методу dropout;
- модели становятся менее чувствительны к начальной инициализации весов.
Описание метода
Опишем устройство метода пакетной нормализации. Пусть на вход некоторому слою нейронной сети поступает вектор размерности : . Нормализуем данный вектор по каждой размерности :
,
где математическое ожидание и дисперсия считаются по всей обучающей выборке. Такая нормализация входа слоя нейронной сети может изменить представление данных в слое. Чтобы избежать данной проблемы, вводятся два параметра сжатия и сдвига нормализованной величины для каждого : , — которые действуют следующим образом:
.
Данные параметры настраиваются в процессе обучения вместе с остальными параметрами модели.
Пусть обучение модели производится с помощью пакетов размера : . Здесь нормализация применяется к каждой компоненте входа с номером отдельно, поэтому в индекс опускается для ясности изложения. Пусть были получены нормализованные значения пакета . После применения операций сжатия и сдвига были получены . Обозначим данную функцию пакетной нормализации следующим образом:
Тогда алгоритм пакетной нормализации можно представить так:
Вход: значения из пакета ; настраиваемые параметры ; константа для вычислительной устойчивости. Выход: // математическое ожидание пакета // дисперсия пакета // нормализация // сжатие и сдвиг
Заметим, что если и , то равен , то есть является тождественным отображением. Таким образом, использование пакетной нормализации не может привести к снижению точности, поскольку оптимизатор просто может использовать нормализацию как тождественное отображение.
Обучение нейронных сетей с пакетной нормализацией
Для обучения нейронных сетей необходимо вычислять градиент функции потерь . В случае использования метода пакетной нормализации градиент вычисляется следующим образом:
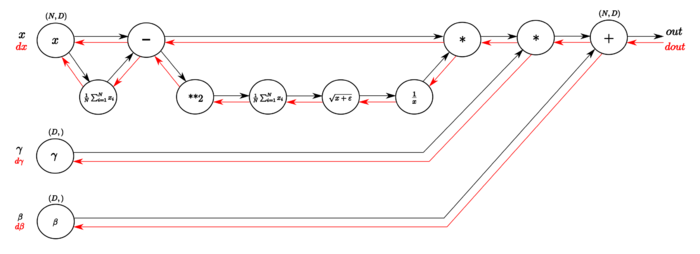
На Рисунке 2 изображен граф вычислений слоя пакетной нормализации алгоритмом обратного распространения ошибки.
В прямом направлении, как и описано в алгоритме метода, из входа вычисляется среднее значение по каждой размерности признакового пространства. Затем полученный вектор средних значение вычитается из каждого элемента обучающей выборки. Далее вычисляется дисперсия, и с помощью нее вычисляется знаменатель для нормализации. Затем полученное значение инвертируется и умножается на разницу входа и средних значений. В конце применяются параметры и .
В обратном направлении вычисляются производные необходимых функций. В следующей таблице подробнее изображены шаги вычисления градиента функции потерь (иллюстрации из статьи, здесь и ):
Пакетная нормализация в свёрточных сетях
Пакетная нормализация может быть применена к любой функции активации. Рассмотрим подробнее случай аффинного преобразования с некоторой нелинейной функцией:
,
где и — настраиваемые параметры модели, а — некоторая нелинейная функция, например cигмоида или ReLU. Данной функцией можно описать как обычные, так и сверточные слои нейронных сетей. Пакетная нормализация применяется сразу перед функцией к . Параметр может быть опущен, так как в дальнейших вычислениях его роль будет играть параметр . Поэтому может быть записано так:
,
где применяется отдельно к каждой размерности с отдельной парой параметров и для каждой размерности.
В случае свёрточных сетей, дополнительно необходима нормализация, чтобы удовлетворить свойство свёрточных сетей, что различные элементы в разных местах одной карты признаков (образ операции свёртки, англ. feature map) должны быть нормализованы одинаково. Чтобы этого добиться, нормализация выполняется совместно над всеми значениями в пакете. Пусть — множество всех значений в карте признаков по всему пакету и всем точкам в карте признаков. Тогда для пакета размера и карты признаков размера размер равен . Тогда параметры и настраиваются для каждой карты признаков отдельно.
Пример
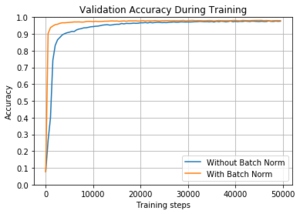
Приведем пример демонстрирующий работу пакетной нормализации. Рассмотрим задачу распознавания рукописных цифр на известном датасете MNIST [3]. Для решения задачи будет использоваться обычная нейронная сеть с скрытыми полносвязными слоями по узлов в каждом. Функция активации — ReLU. Выходной слой содержит узлов. Размер пакета равен . Сравниваются две одинаковые модели, но в первой перед каждым скрытым слоем используется пакетная нормализация, а во второй — нет. Темп обучения равен . Веса инициализированы значениями с малой дисперсией.
На Рисунке 3 изображены два графика, показывающие разницу между моделями. Как видно, обе модели достигли высокой точности, но модель с использованием пакетной нормализации достигла точности более быстрее, почти сразу, и достигла максимума, примерно, уже на итераций. Однако, модель без пакетной нормализации достигла скорости обучения примерно пакетов в секунду, а модель с использованием пакетной нормализации — . Однако, как можно видеть, пакетная нормализация позволяет выполнить меньшее количество итераций и, в итоге, сойтись за меньшее время.
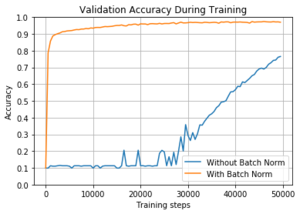
На Рисунке 4 изображен график, сравнивающий точно такие же модели, но с использованием сигмоиды в качестве функции активации. Такая конфигурация моделей требует большего времени, чтобы начать обучение. В итоге, модель обучается, но на это потребовалось более итераций, чтобы получить точность более . При использовании пакетной нормализации получилось достичь точность более примерно за итераций.
Реализации
Механизм пакетной нормализации реализован практически во всех современных инструментариях для машинного обучения, таких как: TensorFlow [4], Keras [5], CNTK [6], Theano [7], PyTorch [8] и т.д.
Приведем пример[9] применения пакетной нормализации с использованием библиотеки TensorFlow на языке программирования Python [10]:
import tensorflow as tf
# ...
is_train = tf.placeholder(tf.bool, name="is_train");
# ...
x_norm = tf.layers.batch_normalization(x, training=is_train)
# ...
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops):
train_op = optimizer.minimize(loss)
Модификации
Существует несколько модификаций и вариаций метода пакетной нормализации:
- Тим Койманс[11] в 2016 г. предложил способ применения пакетной нормализации к рекуррентным нейронным сетям[на 10.01.18 не создан].
- Расширение метода пакетной нормализации было предложено Ликси Хуангом[12] в 2018 г. Метод получил название декоррелированная пакетная нормализация (англ. Decorrelated Batch Normalization). В данном методе кроме операций масштабирования и сдвига была предложено использование специальной функции затирания данных.
- Джимми Лей Ба[13] в 2016 г. предложил метод нормализации слоев (англ. Layer Normalization), который решает проблему выбора размера пакета.
- В работе Сергея Иоффе[14] в 2017 г. было представлено расширение метода пакетной нормализации: пакетная ренормализация (англ. Batch Renormalization). Данный метод улучшает пакетную нормализацию, когда размер пакетов мал и не состоит из независимых данных.
- Метод потоковой нормализации (англ. Streaming Normalization) был предложен Кифэном Ляо[15] в 2016 г. Данный метод убирает два ограничения пакетной нормализации: использование при online-обучении и использование в рекуррентных нейронных сетях.
См. также
Примечания
- ↑ Ioffe S., Szegedy C. — Batch normalization: Accelerating deep network training by reducing internal covariate shift, 2016
- ↑ Метод стохастического градиента
- ↑ Датасет MNIST
- ↑ TensorFlow
- ↑ Keras
- ↑ CNTK
- ↑ Theano
- ↑ PyTorch
- ↑ Batch normalization: theory and how to use it with Tensorflow
- ↑ Язык программирования Python
- ↑ Cooijmans T. — Recurrent batch normalization, 2016
- ↑ Huang L. — Decorrelated Batch Normalization, 2018
- ↑ Ba J. L., Kiros J. R., Hinton G. E. — Layer normalization, 2016
- ↑ Ioffe S. — Batch renormalization: Towards reducing minibatch dependence in batch-normalized models, 2017
- ↑ Liao Q., Kawaguchi K., Poggio T. — Streaming normalization: Towards simpler and more biologically-plausible normalizations for online and recurrent learning, 2016
Источники информации
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- Glossary of Deep Learning: Batch Normalisation
- Understanding the backward pass through Batch Normalization Layer
- Deeper Understanding of Batch Normalization with Interactive Code in Tensorflow
- Batch Normalization in Deep Networks
- Batch Normalization — Lesson