Граф компонент рёберной двусвязности — различия между версиями
м (ё) |
м (Дмитрий Мурзин переименовал страницу Граф компонент реберной двусвязности в Граф компонент рёберной двусвязности: Ёфикация) |
(нет различий)
| |
Версия 23:37, 31 января 2019
| Определение: |
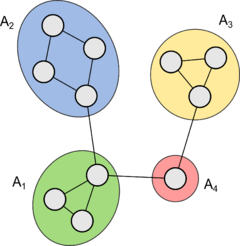
| Пусть граф связен. Обозначим — компоненты рёберной двусвязности, а — мосты . Построим граф , в котором вершинами будут , а рёбрами — , соединяющими соответствующие вершины из соответствующих компонент рёберной двусвязности. Полученный граф называют графом компонент рёберной двусвязности (англ. costal doubly-linked components graph) графа . |
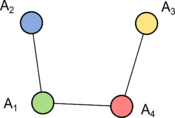
| Лемма: |
В определении, приведенном выше, — дерево. |
| Доказательство: |
|