Теорема о поглощении — различия между версиями
Alina (обсуждение | вклад) |
|||
| Строка 3: | Строка 3: | ||
'''Формулировка''' | '''Формулировка''' | ||
| − | С вероятностью, равной 1, марковская цепь перейдет в поглощающее состояние | + | С вероятностью, равной 1, марковская цепь перейдет в поглощающее состояние, если у нее существует такое состояние. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Доказательство теоремы == | == Доказательство теоремы == | ||
| − | + | Пусть '''''P''''' - матрица переходов, где элемент <tex>p_{ij}</tex> равен вероятности перехода из i-го состояния в j-ое. Она будет выглядеть как матрица из 4-х блоков, где Q - несущественные состояния, а R и I - существенные.(т.к. цепь поглощающая, то из любого несущественного можно попасть в существенное) | |
| − | + | [[Файл:Матрница_перехода.GIF]] | |
| − | |||
| − | |||
| − | |||
| − | + | Пусть вектор <tex>c^{(t)}</tex> - вектор вероятности нахождения на шаге t. | |
| + | Он вычисляется, как произведение вектора на нулевом шаге на матрицу перехода в степени t. | ||
| + | <tex> c^{(t)} = c^{(0)} * P^t</tex> | ||
| + | Рассмотрим, что представляет из себя возведение матрицы P в степень: | ||
| − | + | для t=1 : | |
| + | [[Файл:Матрница перехода (перемножение).GIF]] | ||
| + | Отсюда видно, что <tex> P^n</tex> имеет такой вид, где X - некоторые значения. | ||
| + | [[Файл:Vfnhbwf d n-jq cntgtyb.GIF]] | ||
| − | + | Следовательно нам надо доказать, что <tex>Q^n \xrightarrow{} 0</tex>, при <tex> n\xrightarrow{}+\infty</tex> | |
| − | + | Рассмотрим путь из i-го состояния в поглощающее, равное <tex>m_i</tex>. Пусть <tex>p<1</tex> - вероятность того, что через <tex>m_i</tex> шагов из шага i не попадет в поглощающее состояние. | |
| + | Пусть <tex>m = max(m_i)</tex>, а <tex>p = max(p_i)< 1</tex> | ||
| − | + | Тогда получаем: <tex>\sum_{j} {Q^m_{ij}}\leqslant p</tex> <tex>\Rightarrow</tex> <tex>\sum_{j} {Q^{mk}_{ij}}\leqslant p^k\xrightarrow{k\xrightarrow{}+\infty}0</tex> | |
| − | + | В итоге получаем, что несущественные состояния стремятся к 0, а значит существенные в итоге приходят к 1, т.е. цепь приходит в поглощающее состояние. | |
| − | |||
Версия 00:10, 16 января 2011
Формулировка теоремы
Формулировка
С вероятностью, равной 1, марковская цепь перейдет в поглощающее состояние, если у нее существует такое состояние.
Доказательство теоремы
Пусть P - матрица переходов, где элемент равен вероятности перехода из i-го состояния в j-ое. Она будет выглядеть как матрица из 4-х блоков, где Q - несущественные состояния, а R и I - существенные.(т.к. цепь поглощающая, то из любого несущественного можно попасть в существенное)
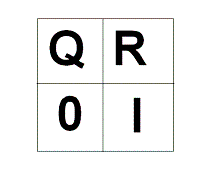
Пусть вектор - вектор вероятности нахождения на шаге t. Он вычисляется, как произведение вектора на нулевом шаге на матрицу перехода в степени t. Рассмотрим, что представляет из себя возведение матрицы P в степень:
для t=1 :
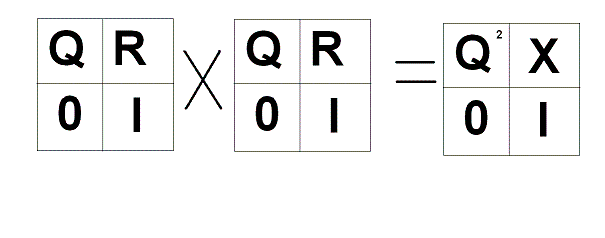
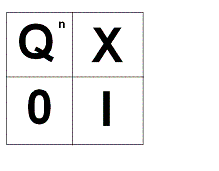
Следовательно нам надо доказать, что , при
Рассмотрим путь из i-го состояния в поглощающее, равное . Пусть - вероятность того, что через шагов из шага i не попадет в поглощающее состояние. Пусть , а
Тогда получаем:
В итоге получаем, что несущественные состояния стремятся к 0, а значит существенные в итоге приходят к 1, т.е. цепь приходит в поглощающее состояние.