Список с пропусками — различия между версиями
Gaporf (обсуждение | вклад) (→Псевдокод) |
Gaporf (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
'''Список с пропусками''' (англ. ''skip list'') — вероятностная структура данных, позволяющая в среднем за <tex>O(\log(n))</tex> времени выполнять операции добавления, удаления и поиска элементов. | '''Список с пропусками''' (англ. ''skip list'') — вероятностная структура данных, позволяющая в среднем за <tex>O(\log(n))</tex> времени выполнять операции добавления, удаления и поиска элементов. | ||
| − | Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов в таком же порядке располагаются на втором, почти четверть | + | Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов в таком же порядке располагаются на втором, почти четверть — на третьем и так далее, но при этом известно, что если элемент расположен на уровне <tex>i</tex>, то он также расположен на всех уровнях, номера которых меньше <tex>i</tex>. |
==Построение== | ==Построение== | ||
| Строка 11: | Строка 11: | ||
Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за <tex>O(\log{n})</tex> времени выполнять операции добавления, удаления и поиска элементов. | Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за <tex>O(\log{n})</tex> времени выполнять операции добавления, удаления и поиска элементов. | ||
| − | На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне | + | На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне — всё элементы с чётными номерами, причём каждый элемент будет ссылаться на соответствующий ему элемент на нижнем уровне. Таким же образом построим и третий уровень, куда будем добавлять только те элементы, номера которых кратны четырём. Аналогичным образом построим и последующие уровни. |
====Псевдокод==== | ====Псевдокод==== | ||
| − | Каждый уровень списка с пропусками содержит отсортированный односвязный список, у | + | Каждый уровень списка с пропусками содержит отсортированный односвязный список, у которого есть начало <tex>\mathtt{head}</tex> и конец <tex>\mathtt{tail}</tex>. Для выполнения операций на списке с пропусками необходимо передавать в качестве аргумента ссылку на начало односвязного списка, расположенного на самом верхнем уровне. |
| − | Элементы односвязного списка | + | Элементы односвязного списка — вершины <tex>\mathtt{node}</tex>, у которых есть <tex>3</tex> поля: |
| − | * <tex>\mathtt{next}</tex> | + | * <tex>\mathtt{next}</tex> — ссылка на следующий элемент списка |
| − | * <tex>\mathtt{key}</tex> | + | * <tex>\mathtt{key}</tex> — ключ, который хранится в данной вершине |
| − | * <tex>\mathtt{down}</tex> | + | * <tex>\mathtt{down}</tex> — ссылка на соответственный элемент, лежащий уровнем ниже |
Также известно, что <tex>\mathtt{head{.}key} = -\infty \ </tex> и <tex>\mathtt{tail{.}key} = \infty</tex>. | Также известно, что <tex>\mathtt{head{.}key} = -\infty \ </tex> и <tex>\mathtt{tail{.}key} = \infty</tex>. | ||
| Строка 26: | Строка 26: | ||
Функция <tex>\ \mathtt{build\_lvl} \ </tex> возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня. | Функция <tex>\ \mathtt{build\_lvl} \ </tex> возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня. | ||
| − | '''list''' build_lvl ('''list''' lvl) | + | '''list''' build_lvl('''list''' lvl) |
'''list''' next_lvl | '''list''' next_lvl | ||
'''node''' i = lvl.head | '''node''' i = lvl.head | ||
| − | '''while''' | + | '''node''' cur = next_lvl.head |
| − | + | '''while''' i <tex>\neq</tex> ''null'' '''and''' i.next <tex>\neq</tex> ''null'' | |
| − | i = i.next.next | + | cur.next = node(key, i, cur.next) <font color=darkgreen>// Конструктор node(key, down, next) возвращает новую вершину с ключом key, ссылками down на нижний и next на следующий элемент</font> |
| + | cur = cur.next | ||
| + | i = i.next.next <font color=darkgreen>// Переход к следующему чётному элементу</font> | ||
'''return''' next_lvl | '''return''' next_lvl | ||
Функция <tex>\ \mathtt{skip\_list} \ </tex> принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе. | Функция <tex>\ \mathtt{skip\_list} \ </tex> принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе. | ||
| − | '''list''' skip_list ('''list''' l): | + | '''list''' skip_list('''list''' l): |
| − | '''list''' lvl = build_lvl(l) | + | '''list''' lvl = build_lvl(l) <font color=darkgreen>// Построение первого уровня</font> |
| − | '''while''' lvl.size > 2 | + | '''while''' lvl.size > 2 |
lvl = build_lvl(lvl) | lvl = build_lvl(lvl) | ||
| − | '''return''' lvl | + | '''return''' lvl <font color=darkgreen>// Возвращает ссылку на начало верхнего уровня</font> |
==Операции над структурой== | ==Операции над структурой== | ||
| Строка 50: | Строка 52: | ||
# Начинаем поиск элемента в самом верхнем уровне | # Начинаем поиск элемента в самом верхнем уровне | ||
# Переходим к следующему элементу списка, пока значение в следующей ячейке меньше | # Переходим к следующему элементу списка, пока значение в следующей ячейке меньше | ||
| − | # Переместиться на один уровень вниз и перейти к шагу <tex>2</tex>. Если мы уже на первом уровне | + | # Переместиться на один уровень вниз и перейти к шагу <tex>2</tex>. Если мы уже на первом уровне — прекратить поиск и вернуть ссылку на текущую вершину |
В конце алгоритма функция вернёт элемент, значение которого не меньше ключа <tex>\mathtt{key}</tex> или ссылку на конец списка на первом уровне. | В конце алгоритма функция вернёт элемент, значение которого не меньше ключа <tex>\mathtt{key}</tex> или ссылку на конец списка на первом уровне. | ||
| Строка 60: | Строка 62: | ||
Функция <tex>\mathtt{find}</tex> возвращает ссылку на элемент, значение которого не меньше <tex>\mathtt{key}</tex>. В случае, если все элементы в списке с пропусками меньше <tex>\mathtt{key}</tex>, то возвращается ссылка на конец списка с пропусками. | Функция <tex>\mathtt{find}</tex> возвращает ссылку на элемент, значение которого не меньше <tex>\mathtt{key}</tex>. В случае, если все элементы в списке с пропусками меньше <tex>\mathtt{key}</tex>, то возвращается ссылка на конец списка с пропусками. | ||
| − | '''T''' find ('''node''' res, '''K''' key) | + | '''T''' find('''node''' res, '''K''' key) |
| − | '''while''' res.key < key | + | '''while''' res.key < key |
| − | res = res.next | + | res = res.next |
| − | '''if''' res.down = ''null'' | + | '''if''' res.down = ''null'' <font color=darkgreen>// Если мы находимся на первом уровне</font> |
| − | '''return''' res | + | '''return''' res <font color=darkgreen>// Мы нашли искомый элемент</font> |
| − | '''return''' find(res.down, key) | + | '''return''' find(res.down, key) <font color=darkgreen>// Иначе спустимся на один уровень ниже</font> |
Для того, чтобы найти элемент с ключом <tex>\mathtt{key}</tex> в списке с пропусками <tex>\mathtt{skip}</tex> необходимо запустить <tex>\mathtt{find}</tex> следующим образом | Для того, чтобы найти элемент с ключом <tex>\mathtt{key}</tex> в списке с пропусками <tex>\mathtt{skip}</tex> необходимо запустить <tex>\mathtt{find}</tex> следующим образом | ||
| Строка 74: | Строка 76: | ||
Алгоритм вставки элементов в список с пропусками состоит из следующих шагов: | Алгоритм вставки элементов в список с пропусками состоит из следующих шагов: | ||
# Начинаем вставку на самом верхнем уровне | # Начинаем вставку на самом верхнем уровне | ||
| − | # Пока | + | # Пока значение следующего элемента меньше ключа — переходим к следующему элементу. |
| − | # Если мы на первом уровне | + | # Если мы на первом уровне — вставляем элемент. Иначе спускаемся ниже и возвращаемся к шагу <tex>2</tex>. |
| − | # Кидаем монетку и если выпал «Орёл», то возвращаем ссылку на текущий элемент, иначе | + | # Кидаем монетку и если выпал «Орёл», то возвращаем ссылку на текущий элемент, иначе — ''null''. Если мы были не на первом уровне и нам вернули ''null'' — возвращаем его без броска монетки. |
Отдельно стоит обработать случай, когда вставка нового элемента увеличивает число уровней. Тогда необходимо создать ещё один отсортированный список, в котором будет всего один текущий элемент, и не забыть присвоить списку с пропусками новую ссылку на верхний уровень. Будем считать, что вставка каждого нового элемента увеличивает число уровней не более, чем на один. | Отдельно стоит обработать случай, когда вставка нового элемента увеличивает число уровней. Тогда необходимо создать ещё один отсортированный список, в котором будет всего один текущий элемент, и не забыть присвоить списку с пропусками новую ссылку на верхний уровень. Будем считать, что вставка каждого нового элемента увеличивает число уровней не более, чем на один. | ||
====Псевдокод==== | ====Псевдокод==== | ||
| − | Функция <tex>\mathtt{insert}</tex> возвращаем ссылку на вставленный элемент в списке, в котором находится <tex>\mathtt{res}</tex>, или ''null'', если на монете | + | Функция <tex>\mathtt{insert}</tex> возвращаем ссылку на вставленный элемент в списке, в котором находится <tex>\mathtt{res}</tex>, или ''null'', если на монете выпала «Решка». |
'''node''' insert('''node''' res, '''K''' key) | '''node''' insert('''node''' res, '''K''' key) | ||
| − | '''while''' res.next <tex>\neq</tex> ''null'' '''and''' res.next. | + | '''while''' res.next <tex>\neq</tex> ''null'' '''and''' res.next.key < key |
| − | res = res.next | + | res = res.next |
| + | '''node''' down_node | ||
'''if''' res.down = ''null'' | '''if''' res.down = ''null'' | ||
| − | + | down_node = ''null'' | |
| − | + | '''else''' | |
| − | + | down_node = insert(res.down, key) | |
| − | + | '''if''' down_node <tex>\neq</tex> ''null'' | |
| − | + | res.next = node(key, down_node, res.next) | |
| − | '''if''' | + | '''if''' random(0, 1) > 0.5 <font color=darkgreen>// Бросок монеты</font> |
| − | res.next = node(key, | ||
| − | '''if''' random(0, 1) > 0.5 | ||
'''return''' res.next | '''return''' res.next | ||
'''return''' ''null'' | '''return''' ''null'' | ||
| Строка 111: | Строка 112: | ||
Алгоритм удаления элемента выглядит следующим образом: | Алгоритм удаления элемента выглядит следующим образом: | ||
# Начинаем удалять элемент с верхнего уровня | # Начинаем удалять элемент с верхнего уровня | ||
| − | # Если мы на первом уровне | + | # Переходим к следующему элементу, пока значение следующего элемента меньше ключа |
| − | + | # Если элемент существует на данном уровне — удаляем его с этого уровня. Если мы не на первом уровне, то удаляем элемент ещё с нижнего уровня. | |
====Псевдокод==== | ====Псевдокод==== | ||
| + | '''function''' delete('''node''' res, '''K''' key) | ||
| + | '''while''' res.next <tex>\neq</tex> ''null'' '''and''' res.next.key < key | ||
| + | res = res.next | ||
| + | '''if''' res.down <tex>\neq</tex> ''null'' | ||
| + | delete(res.down, key) | ||
| + | '''if''' res.next <tex>\neq</tex> ''null'' '''and''' res.next.key = key | ||
| + | res.next = res.next.next; | ||
==Использование нечестной монеты== | ==Использование нечестной монеты== | ||
| Строка 119: | Строка 127: | ||
Для крайних распределений: | Для крайних распределений: | ||
| − | * <tex>\{0, 1\}</tex> | + | * <tex>\{0, 1\}</tex> — <tex>O(n)</tex> — поиск, добавление и удаления элемента, поскольку мы вместо нескольких списков используем по факту один. |
| − | * <tex>\{1, 0\}</tex> | + | * <tex>\{1, 0\}</tex> — зависит от реализации алгоритма. Если при каждой вставке у нас образуется не более одного уровня, то количество уровней будет равным <tex>n</tex>, значит время поиска будет равным <tex>O(n)</tex>. |
==Применение== | ==Применение== | ||
| Строка 138: | Строка 146: | ||
}} | }} | ||
| − | Для решения данной задачи воспользуемся списком с пропусками. Когда нам приходит запрос первого типа, то мы просто добавляем числа <tex>L</tex> и <tex>R</tex> в список с пропусками (если какое-то из чисел уже было добавлено, то второй раз мы его не добавляем) | + | Для решения данной задачи воспользуемся списком с пропусками. Когда нам приходит запрос первого типа, то мы просто добавляем числа <tex>L</tex> и <tex>R</tex> в список с пропусками (если какое-то из чисел уже было добавлено, то второй раз мы его не добавляем). После этого идём с самого верхнего уровня и до нижнего и если два элемента на каком-либо уровне находятся между <tex>L</tex> и <tex>R</tex>, то прибавляем <tex>1</tex> к отрезку и переходим к следующему элементу на том же уровне, иначе спускаемся вниз. Когда нам приходит запрос второго типа — на каждом уровне находим такие два элемента, что <tex>x</tex> лежит между ними, и к ответу прибавляем значение на данном отрезке. Итого оба запросы мы обрабатываем за <tex>O(\log{n})</tex>. |
==См. также== | ==См. также== | ||
Версия 13:01, 24 марта 2019
Список с пропусками (англ. skip list) — вероятностная структура данных, позволяющая в среднем за времени выполнять операции добавления, удаления и поиска элементов.
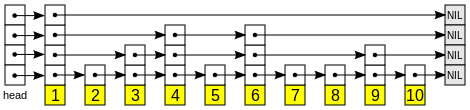
Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов в таком же порядке располагаются на втором, почти четверть — на третьем и так далее, но при этом известно, что если элемент расположен на уровне , то он также расположен на всех уровнях, номера которых меньше .
Содержание
Построение
Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за времени выполнять операции добавления, удаления и поиска элементов.
На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне — всё элементы с чётными номерами, причём каждый элемент будет ссылаться на соответствующий ему элемент на нижнем уровне. Таким же образом построим и третий уровень, куда будем добавлять только те элементы, номера которых кратны четырём. Аналогичным образом построим и последующие уровни.
Псевдокод
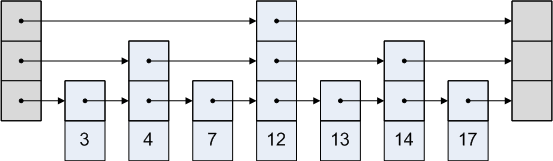
Каждый уровень списка с пропусками содержит отсортированный односвязный список, у которого есть начало и конец . Для выполнения операций на списке с пропусками необходимо передавать в качестве аргумента ссылку на начало односвязного списка, расположенного на самом верхнем уровне.
Элементы односвязного списка — вершины , у которых есть поля:
- — ссылка на следующий элемент списка
- — ключ, который хранится в данной вершине
- — ссылка на соответственный элемент, лежащий уровнем ниже
Также известно, что и .
Функция возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня.
list build_lvl(list lvl)
list next_lvl
node i = lvl.head
node cur = next_lvl.head
while i null and i.next null
cur.next = node(key, i, cur.next) // Конструктор node(key, down, next) возвращает новую вершину с ключом key, ссылками down на нижний и next на следующий элемент
cur = cur.next
i = i.next.next // Переход к следующему чётному элементу
return next_lvl
Функция принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе.
list skip_list(list l):
list lvl = build_lvl(l) // Построение первого уровня
while lvl.size > 2
lvl = build_lvl(lvl)
return lvl // Возвращает ссылку на начало верхнего уровня
Операции над структурой
Поиск элемента
Алгоритм поиска элементе в списке с пропусками состоит из следующих операций:
- Начинаем поиск элемента в самом верхнем уровне
- Переходим к следующему элементу списка, пока значение в следующей ячейке меньше
- Переместиться на один уровень вниз и перейти к шагу . Если мы уже на первом уровне — прекратить поиск и вернуть ссылку на текущую вершину
В конце алгоритма функция вернёт элемент, значение которого не меньше ключа или ссылку на конец списка на первом уровне.
Если в качестве случайного источника мы будем использовать честную монету, то в среднем случае будет уровне. На самом верхнем уровне будет не более двух элементов. Тогда на каждом уровне в среднем нужно проверить не более двух элементов (в противном случае могли бы вместо двух нижних элементов проверить ещё один уровнем выше). Уровней всего , откуда вытекает оценка времени поиска элемента в .
Псевдокод
Функция возвращает ссылку на элемент, значение которого не меньше . В случае, если все элементы в списке с пропусками меньше , то возвращается ссылка на конец списка с пропусками.
T find(node res, K key)
while res.key < key
res = res.next
if res.down = null // Если мы находимся на первом уровне
return res // Мы нашли искомый элемент
return find(res.down, key) // Иначе спустимся на один уровень ниже
Для того, чтобы найти элемент с ключом в списке с пропусками необходимо запустить следующим образом
find(skip.head, key)
Вставка элемента
Алгоритм вставки элементов в список с пропусками состоит из следующих шагов:
- Начинаем вставку на самом верхнем уровне
- Пока значение следующего элемента меньше ключа — переходим к следующему элементу.
- Если мы на первом уровне — вставляем элемент. Иначе спускаемся ниже и возвращаемся к шагу .
- Кидаем монетку и если выпал «Орёл», то возвращаем ссылку на текущий элемент, иначе — null. Если мы были не на первом уровне и нам вернули null — возвращаем его без броска монетки.
Отдельно стоит обработать случай, когда вставка нового элемента увеличивает число уровней. Тогда необходимо создать ещё один отсортированный список, в котором будет всего один текущий элемент, и не забыть присвоить списку с пропусками новую ссылку на верхний уровень. Будем считать, что вставка каждого нового элемента увеличивает число уровней не более, чем на один.
Псевдокод
Функция возвращаем ссылку на вставленный элемент в списке, в котором находится , или null, если на монете выпала «Решка».
node insert(node res, K key)
while res.next null and res.next.key < key
res = res.next
node down_node
if res.down = null
down_node = null
else
down_node = insert(res.down, key)
if down_node null
res.next = node(key, down_node, res.next)
if random(0, 1) > 0.5 // Бросок монеты
return res.next
return null
return null
Для того, чтобы вставить элемент с ключом в список с пропусками необходимо вызвать следующую функцию
function insert_element(list skip, K key)
node res = insert(skip.head, key)
if res null
list lvl;
lvl.head.next = node(key, res, lvl.tail)
skip = lvl
Удаление элемента
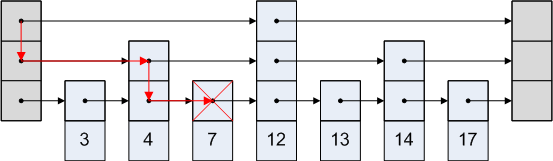
Алгоритм удаления элемента выглядит следующим образом:
- Начинаем удалять элемент с верхнего уровня
- Переходим к следующему элементу, пока значение следующего элемента меньше ключа
- Если элемент существует на данном уровне — удаляем его с этого уровня. Если мы не на первом уровне, то удаляем элемент ещё с нижнего уровня.
Псевдокод
function delete(node res, K key)
while res.next null and res.next.key < key
res = res.next
if res.down null
delete(res.down, key)
if res.next null and res.next.key = key
res.next = res.next.next;
Использование нечестной монеты
Вместо честной монеты с распределением можно взять в качестве случайного источника нечестную монету с распределением (с вероятностью выпадает «Орёл»). Тогда математическим ожиданием количества элементов на уровне будет . Время поиска будет равно (на -ом уровне элементов будет почти в раз больше, чем на -ом, значит на каждом уровне пройдём не более элементов, а уровней всего ).
Для крайних распределений:
- — — поиск, добавление и удаления элемента, поскольку мы вместо нескольких списков используем по факту один.
- — зависит от реализации алгоритма. Если при каждой вставке у нас образуется не более одного уровня, то количество уровней будет равным , значит время поиска будет равным .
Применение
Список с пропусками применяется во многих приложениях, поскольку имеет ряд преимуществ.
- Быстрая вставка элемента, поскольку не требуется каким-либо образом изменять другие элементы (только предыдущий элемент)
- Проще реализовать, чем сбалансированные деревья или хеш-таблицы
- Следующий элемент достаётся за (при условии, что у нас есть ссылка не текущий)
- Легко модифицировать под различные задачи
Нахождение всех интервалов, покрывающих данную точку
| Задача: |
Поступают запросы двух видов:
|
Для решения данной задачи воспользуемся списком с пропусками. Когда нам приходит запрос первого типа, то мы просто добавляем числа и в список с пропусками (если какое-то из чисел уже было добавлено, то второй раз мы его не добавляем). После этого идём с самого верхнего уровня и до нижнего и если два элемента на каком-либо уровне находятся между и , то прибавляем к отрезку и переходим к следующему элементу на том же уровне, иначе спускаемся вниз. Когда нам приходит запрос второго типа — на каждом уровне находим такие два элемента, что лежит между ними, и к ответу прибавляем значение на данном отрезке. Итого оба запросы мы обрабатываем за .
См. также
- Список
- Рандомизированное бинарное дерево поиска
- Поисковые структуры данных
- Skip quadtree
- Skip graph — структура данных, основанная на списке с пропусками