Иерархия порядков сообщений — различия между версиями
Yeputons (обсуждение | вклад) (Новая страница: «В распределённых системах могут быть разные гарантии порядка доставки отправленных соо…») |
Yeputons (обсуждение | вклад) |
||
| Строка 41: | Строка 41: | ||
Q -------b'---b-- | Q -------b'---b-- | ||
</pre> | </pre> | ||
| + | |||
| + | == Синхронный порядок == | ||
Версия 09:42, 3 июня 2019
В распределённых системах могут быть разные гарантии порядка доставки отправленных сообщений. Более того: иногда программисты могут неявно предполагать тот или иной порядок и очень удивляться, когда он нарушается.
Мы рассматриваем четыре гарантии порядка сообщений, от более слабых к более сильным:
- Асинхронная передачи: никаких гарантий, только exactly-once delivery
- FIFO (First In First Out order)
- Причинно-согласованный порядок (causally consistent ordering, от слова cause, а не casual)
- Синхронный порядок
Можно использовать различные алгоритмы, чтобы получить из более слабой гарантии более сильную.
При добавлении multicast/broadcast сообщений возникают свои проблемы, там нужно смотреть на общий порядок сообщений.
Содержание
FIFO
Не существует пары сообщений $m, n \in M$ таких, что $snd(m) < snd(n) \land rcv(n) < rcv(m)$ (тут $<$ работает только если два события произошли в одном процессе).
Переформулировка: для каждой упорядоченной пары процессов $(A, B)$ сообщения приходят к $B$ в том же порядке, в котором они отправлены $A$.
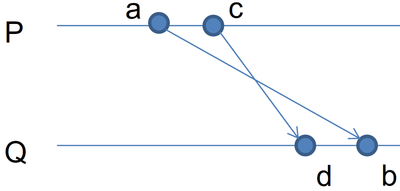
Пример нарушения:
Причинно-согласованный порядок
Как FIFO, только вместо $<$ написали $\to$: не существует пары сообщений $m, n \in M$ таких, что $snd(m) \to snd(n) \land rcv(n) \to rcv(m)$.
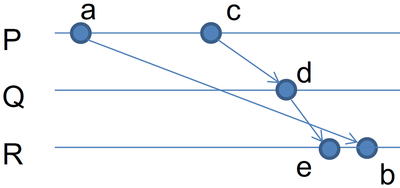
Пример нарушения (пара сообщений $m=(a, b)$ и $n=(d, e)$):
Неверная переформулировка
На лекции не было, но может казаться правдоподобным.
Если есть события $a, a', b, b'$, причём $a<a'$, $proc(b)=proc(b')$ (взяли пару процессов и два события в каждом), $a\to b$ и $a' \to b'$ (взяли цепочки сообщений между ними), то $b < b'$ (порядок сообщений не меняется).
Проблема в том, что $a \to b$ может начаться не с сообщения, а с нескольких переходов внутри $proc(a)$:
P --a---a'--x----
\ \
Q -------b'---b--