Лексикографический порядок — различия между версиями
Shersh (обсуждение | вклад) м (мелочи в псевдокоде) |
|||
| Строка 3: | Строка 3: | ||
Тогда последовательность <tex> ~A </tex> '''лексикографически меньше''' (англ. ''lexicographically less'') последовательности <tex> ~B </tex>, если выполняется одно из двух условий: | Тогда последовательность <tex> ~A </tex> '''лексикографически меньше''' (англ. ''lexicographically less'') последовательности <tex> ~B </tex>, если выполняется одно из двух условий: | ||
*<tex> n < m </tex> и при этом <tex> a_i = b_i </tex> для всех <tex>i \in [1 .. n] </tex>, | *<tex> n < m </tex> и при этом <tex> a_i = b_i </tex> для всех <tex>i \in [1 .. n] </tex>, | ||
| − | * <tex> \ | + | * <tex> \exists k\leqslant \min(n, m): a_k < b_k </tex> и при этом <tex> \forall j : j < k ~a_j = b_j </tex>. |
}} | }} | ||
Версия 22:17, 16 июня 2019
| Определение: |
| Пусть даны две последовательности и
Тогда последовательность лексикографически меньше (англ. lexicographically less) последовательности , если выполняется одно из двух условий:
|
Приведем псевдокод сравнения последовательностей из элементов множества Т:
function compare(A, B : list <T>): Ord // Возвращает "LT", если A < B, "GT", если A > B, или "EQ", если последовательности равны
for i = 1 to min(len(A), len(B))
if A[i] < B[i] // i-й элемент А меньше i-го элемента B, но префиксы длины i - 1 равны
return LT
if A[i] > B[i] // i-й элемент А больше i-го элемента B, но префиксы длины i - 1 равны
return GT
if len(A) < len(B) // А — префикс В, но не равна ей
return LT
if len(A) > len(B) // В — префикс А, но не равна ей
return GT
return EQ // Длины последовательностей и все элементы равны
| Определение: |
| Последовательности записаны в лексикографическом порядке (англ. lexicographical order), если для любых выполняется неравенство , где и последовательности с номерами и . |
Например, слово "сон" лексикографически меньше слова "сонный", так как оно является его префиксом. Слово "низ" лексикографически меньше слова "нос", поскольку первые символы совпадают, а второй символ первого слова меньше, чем второй символ второго.
Примеры
- Перестановки (светло-фиолетовым выделен общий префикс, темно-фиолетовым первый отличный элемент, так как , то первая перестановка лексикографически меньше)
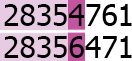
|
- Сочетания (так как , то первое сочетание лексикографически меньше)
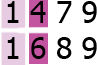
|
- Разбиение на слагаемые (так как , то первое разбиение на слагаемые лексикографически меньше)
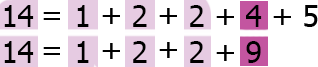
|
- Последовательность чисел в любой системе счисления, записанных в фиксированной разрядной сетке (, , , , , , , ).
- Порядок слов в словаре. Предполагается, что буквы можно сравнивать, сравнивая их номера в алфавите. Тогда лексикографический порядок — это, например, , , , , , .
- Эти слова тоже записаны в лексикографическом порядке: , , , , .
См. также
- Генерация комбинаторных объектов в лексикографическом порядке
- Получение предыдущего объекта
- Получение следующего объекта