Определение сети, потока

Определение сети

Определение:

Сеть (англ. flow network) [math]G=(V,E)[/math] представляет собой ориентированный граф, в котором каждое ребро [math](u,v)\in E[/math] имеет положительную пропускную способность (англ. capacity) [math]c(u,v)\gt 0[/math]. Если [math](u,v)\notin E[/math], предполагается что [math]c(u,v)=0[/math].

В транспортной сети выделяются две вершины: исток [math]s[/math] и сток [math]t[/math].

Определение потока

Определение:

Потоком (англ. flow) [math]f[/math] в [math]G[/math] является действительная функция [math]f\colon V\times V\to R[/math], удоволетворяющая условиям: 1) [math]f(u,v)=-f(v,u)[/math] (антисимметричность); 2) [math]|f(u,v)| \leqslant c(u,v)[/math] (ограничение пропускной способности), если ребра нет, то [math]f(u,v)=0[/math]; 3) [math]\sum\limits_v f(u,v)=0[/math] для всех вершин [math]u[/math], кроме [math]s[/math] и [math]t[/math] (закон сохранения потока). Величина потока [math]f[/math] определяется как [math]|f|=\sum\limits_{v\in V} f(s,v)[/math].

Также существует альтернативное определение (по Асанову), не вводящее антисимметричность (зачастую, из-за этого с ним труднее работать):

Определение:

Потоком [math]f[/math] в сети [math]G=(V,E,c)[/math] называется функция [math]f\colon E\to R[/math], удоволетворяющая условиям: 1) [math]0 \leqslant f(e) \leqslant c(e)[/math] для всех [math]e\in E[/math]; 2) [math]f(v-) = f(v+)[/math] для всех [math]v\in V, v\ne s, v\ne t[/math], где [math]f(v-)=\sum\limits_{w\in v-} f(w,v), f(v+)=\sum\limits_{w\in v+} f(v,u)[/math]. Здесь [math] s [/math] — источник, а [math] t [/math] — сток сети [math]G[/math] ([math]s[/math] имеет нулевую степень захода, а [math]t[/math] имеет нулевую степень исхода); через [math]v+[/math] обозначено множество вершин, к которым идут дуги из вершины [math]v[/math]; через [math]v-[/math] обозначено множество вершин, из которых идут дуги в вершину [math]v[/math]; [math]c(e)[/math] называется пропускной способностью дуги [math]e[/math] и неотрицательно.

Число [math]f(v,w)[/math] можно интерпретировать, например, как количество жидкости, поступающей из [math]v[/math] в [math]w[/math] по дуге [math](v,w)[/math]. С этой точки зрения значение [math]f(v-)[/math] может быть интерпретировано как поток, втекающий в вершину [math]v[/math], а [math] f(v+) [/math] — вытекающий из [math] v [/math]. Условие 1) называется условием ограничения по пропускной способности, а условие 2) — условием сохранения потока в вершинах; иными словами, поток, втекающий в вершину [math] v [/math], отличную от [math] s [/math] или [math] t [/math], равен вытекающему из неё потоку.

Пример

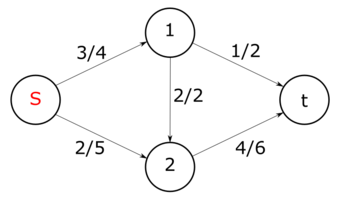
Пример сети с источником [math]s[/math] и стоком [math]t[/math].

Первое число означает величину потока, второе — пропускную способность ребра. Отрицательные величины потока не указаны (так как они мгновенно получаются из антисимметричности: [math]f(u,v)=-f(v,u)[/math]). Сумма входящих рёбер везде (кроме источника и стока) равна сумме исходящих и на то, что в общем [math]c(u,v) \neq c(v, u)[/math]. Кроме того, величина потока на ребре никогда не превышает пропускную способность этого ребра.

Величина потока в этом примере равна [math] 3 + 2 = 5 [/math] (считаем от вершины [math]s[/math]).

Источники информации

• Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
• Асанов М. О., Баранский В. А., Расин В. В. — Дискретная математика: Графы, матроиды, алгоритмы: Учебное пособие. 2-е изд., испр. и доп. — СПб.: Издательство "Лань", 2010. — 368 с.: ил. — (Учебники для вузов. Специальная литература). ISBN 978-5-8114-1068-2
• Википедия [math]-[/math] Транспортная сеть
• Wikipedia [math]-[/math] Flow network