Метод четырёх русских для умножения матриц — различия между версиями
| (не показано 58 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | = | + | {{Задача |
| − | + | |definition = Дано две квадратных матрицы <tex>A_{[n \times n]}</tex> и <tex>B_{[n \times n]}</tex>, | |
| − | + | состоящие из нулей и единиц. Нужно найти их произведение. При этом, все операции выполняются по модулю <tex>2</tex>. | |
| − | состоящие из нулей и единиц. Нужно найти их произведение. При этом, все операции выполняются по модулю <tex>2</tex>. | + | }} |
| − | + | </noinclude> | |
| + | <includeonly>{{#if: {{{neat|}}}| | ||
| + | <div style="background-color: #fcfcfc; float:left;"> | ||
| + | <div style="background-color: #ddd;">'''Задача:'''</div> | ||
| + | <div style="border:1px dashed #2f6fab; padding: 8px; font-style: italic;">{{{definition}}}</div> | ||
| + | </div>| | ||
| + | <table border="0" width="100%"> | ||
| + | <tr><td style="background-color: #ddd">'''Задача:'''</td></tr> | ||
| + | <tr><td style="border:1px dashed #2f6fab; padding: 8px; background-color: #fcfcfc; font-style: italic;">{{{definition}}}</td></tr> | ||
| + | </table>}} | ||
| + | </includeonly> | ||
== Простое решение == | == Простое решение == | ||
| − | Если мы будем считать произведение матриц <tex>C = A \cdot B</tex> по определению | + | Если мы будем считать произведение матриц <tex>C = A \cdot B</tex> по определению <tex dpi=130>\left(c_{i, j} = \sum\limits_{k = 1}^n a_{i,k}b_{k,j}\right)</tex>, то сложность работы алгоритма составит <tex>O(n^3)</tex> {{---}} каждый из <tex>n^2</tex> элементов результирующей матрицы <tex>C</tex> вычисляется за время, пропорциональное <tex>n</tex>. |
Сейчас будет показано, как немного уменьшить это время. | Сейчас будет показано, как немного уменьшить это время. | ||
| − | |||
== Сжатие матриц == | == Сжатие матриц == | ||
| Строка 19: | Строка 28: | ||
Аналогично поступим с матрицей <tex>B</tex>, вместо строк деля столбцы. Получим матрицу <tex dpi=140>B'_{\lceil\frac nk\rceil\times n}</tex>. | Аналогично поступим с матрицей <tex>B</tex>, вместо строк деля столбцы. Получим матрицу <tex dpi=140>B'_{\lceil\frac nk\rceil\times n}</tex>. | ||
| − | Теперь, если вместо произведения матриц <tex>A</tex> и <tex>B</tex> считать произведение новых матриц <tex>A'</tex> и <tex>B'</tex>, воспользовавшись посчитанными скалярными произведениями, то каждый элемент матрицы <tex>C</tex> будет получаться уже за время, пропорциональное <tex>\lceil \ | + | Теперь, если вместо произведения матриц <tex>A</tex> и <tex>B</tex> считать произведение новых матриц <tex>A'</tex> и <tex>B'</tex>, воспользовавшись посчитанными скалярными произведениями, то каждый элемент матрицы <tex>C</tex> будет получаться уже за время, пропорциональное <tex>\lceil \dfrac{n}{k} \rceil</tex> вместо <tex>n</tex>, и время произведения матриц сократится с <tex>O(n^3)</tex> до <tex>O(n^2 \cdot\dfrac nk) = O(\dfrac{n^3}{k}) </tex>. |
| − | == Оценка | + | == Оценка сложности алгоритма и выбор k == |
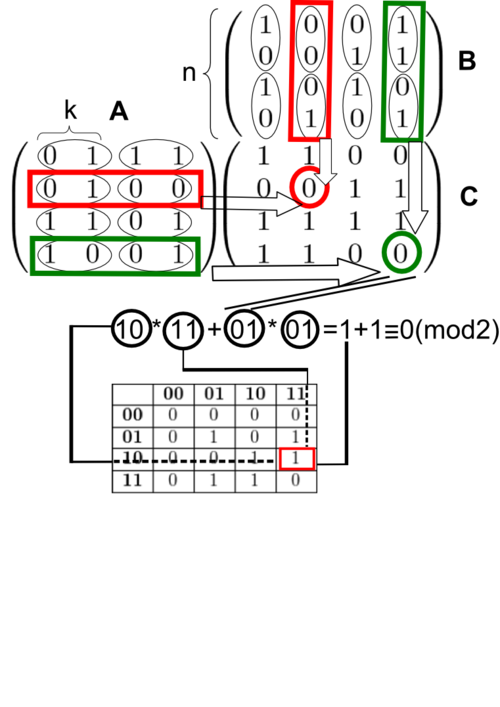
| + | [[Файл:exampleFourRussiansAlgoFinalPicture.png|500px|right]] | ||
| − | Оценим | + | Оценим асимптотику данного алгоритма. |
* Предподсчёт скалярных произведений работает за <tex>O(2^{2k}k)</tex>. | * Предподсчёт скалярных произведений работает за <tex>O(2^{2k}k)</tex>. | ||
| − | * Создание матриц <tex>A'</tex> и <tex>B'</tex> {{---}} <tex>O(n^2)</tex> | + | * Создание матриц <tex>A'</tex> и <tex>B'</tex> {{---}} <tex>O(n^2)</tex>. |
| − | * Перемножение полученных матриц {{---}} <tex | + | * Перемножение полученных матриц {{---}} <tex>O(\dfrac{n^3}{k})</tex>. |
| + | |||
| + | Итого: <tex>O(2^{2k}k) + O(\dfrac{n^3}{k})</tex>. | ||
| + | Выбрав <tex>k = \log n </tex>, получаем требуемую асимптотику <tex>O(n^2 \log n) + O(\dfrac{n^3}{\log n}) = O(\dfrac{n^3}{\log n})</tex> | ||
| + | |||
| + | == Пример работы алгоритма == | ||
| + | |||
| + | Рассмотрим работу алгоритма на примере перемножения двух матриц <tex> A </tex> и <tex> B </tex>, где | ||
| + | |||
| + | <tex> A = </tex> | ||
| + | <tex> | ||
| + | \left(\begin{array}{cccc} | ||
| + | 0 & 1 & 1 & 1 \\ | ||
| + | 0 & 1 & 0 & 0 \\ | ||
| + | 1 & 1 & 0 & 1 \\ | ||
| + | 1 & 0 & 0 & 1 | ||
| + | \end{array}\right) | ||
| + | </tex> | ||
| + | , <tex> B = </tex> | ||
| + | <tex> | ||
| + | \left(\begin{array}{cccc} | ||
| + | 1 & 0 & 0 & 1 \\ | ||
| + | 0 & 0 & 1 & 1 \\ | ||
| + | 1 & 0 & 1 & 0 \\ | ||
| + | 0 & 1 & 0 & 1 | ||
| + | \end{array}\right) | ||
| + | </tex> | ||
| + | |||
| + | <tex> k = \log_2 n = \log_2 4 = 2</tex>, то предподсчитаем все скалярные произведения: | ||
| + | |||
| + | Для удобства каждому битовому вектору будет соответствовать двоичное число с ведущими нулями, т.е. в данном случае имеем числа <tex> 00 </tex>, <tex> 01 </tex>, <tex> 10 </tex>, <tex> 11 </tex>. Ниже приведена таблица, в которой записаны все искомые произведения: | ||
| − | + | <tex> | |
| − | + | \begin{array}{|c|c|c|c|c|} | |
| + | \hline | ||
| + | & \textbf{00} & \textbf{01} & \textbf{10} & \textbf{11} \\ | ||
| + | \hline | ||
| + | \textbf{00} & 0 & 0 & 0 & 0 \\ | ||
| + | \hline | ||
| + | \textbf{01} & 0 & 1 & 0 & 1 \\ | ||
| + | \hline | ||
| + | \textbf{10} & 0 & 0 & 1 & 1 \\ | ||
| + | \hline | ||
| + | \textbf{11} & 0 & 1 & 1 & 0\\ | ||
| + | \hline | ||
| + | \end{array} | ||
| + | </tex> | ||
| − | + | Согласно соглашению относительно битовых векторов и двоичных чисел получим новые матрицы <tex> A' </tex> и <tex> B' </tex>: | |
| − | <tex> | + | <tex> A' = </tex> |
| + | <tex> | ||
| + | \left(\begin{array}{cccc} | ||
| + | 01 & 11 \\ | ||
| + | 01 & 00 \\ | ||
| + | 11 & 01 \\ | ||
| + | 10 & 01 | ||
| + | \end{array}\right) | ||
| + | </tex> | ||
| + | , | ||
| + | <tex> B' = </tex> | ||
| + | <tex> | ||
| + | \left(\begin{array}{cccc} | ||
| + | 10 & 00 & 01 & 11 \\ | ||
| + | 10 & 01 & 10 & 01 | ||
| + | \end{array}\right) | ||
| + | </tex> | ||
| − | + | Перемножим эти матрицы по модулю два с использованием нашего предпосчета: | |
| − | <tex> | + | <tex> C = A' \times B' = </tex> |
| + | <tex> | ||
| + | \left(\begin{array}{cccc} | ||
| + | 1 & 1 & 0 & 0 \\ | ||
| + | 0 & 0 & 1 & 1 \\ | ||
| + | 1 & 1 & 1 & 1 \\ | ||
| + | 1 & 1 & 0 & 0 | ||
| + | \end{array}\right) | ||
| + | </tex> | ||
| − | + | Матрица <tex> C </tex> {{---}} искомая. | |
| − | + | == Источники информации == | |
| − | + | * ''Gregory V. Bard'' — ''Accelerating Cryptanalysis with the Method of Four Russians''. July 22, 2006. Страница 5 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Динамическое программирование]] | [[Категория: Динамическое программирование]] | ||
| + | [[Категория: Способы оптимизации методов динамического программирования]] | ||
Версия 18:07, 8 октября 2019
| Задача: |
| Дано две квадратных матрицы и , состоящие из нулей и единиц. Нужно найти их произведение. При этом, все операции выполняются по модулю . |
Содержание
Простое решение
Если мы будем считать произведение матриц по определению , то сложность работы алгоритма составит — каждый из элементов результирующей матрицы вычисляется за время, пропорциональное .
Сейчас будет показано, как немного уменьшить это время.
Сжатие матриц
Для выполнения сжатия матриц выполним следующий предподсчёт : для всех возможных пар двоичных векторов длины подсчитаем и запомним их скалярное произведение по модулю .
Возьмём первую матрицу. разделим каждую её строку на куски размера . Для каждого куска определим номер двоичного вектора, который соответствует числам, находящимся на этом куске. Если кусок получился неравным по длине (последний кусок строки), то будем считать, что в конце в нём идут не влияющие на умножение нули. Получим матрицу .
Аналогично поступим с матрицей , вместо строк деля столбцы. Получим матрицу .
Теперь, если вместо произведения матриц и считать произведение новых матриц и , воспользовавшись посчитанными скалярными произведениями, то каждый элемент матрицы будет получаться уже за время, пропорциональное вместо , и время произведения матриц сократится с до .
Оценка сложности алгоритма и выбор k
Оценим асимптотику данного алгоритма.
- Предподсчёт скалярных произведений работает за .
- Создание матриц и — .
- Перемножение полученных матриц — .
Итого: . Выбрав , получаем требуемую асимптотику
Пример работы алгоритма
Рассмотрим работу алгоритма на примере перемножения двух матриц и , где
,
, то предподсчитаем все скалярные произведения:
Для удобства каждому битовому вектору будет соответствовать двоичное число с ведущими нулями, т.е. в данном случае имеем числа , , , . Ниже приведена таблица, в которой записаны все искомые произведения:
Согласно соглашению относительно битовых векторов и двоичных чисел получим новые матрицы и :
,
Перемножим эти матрицы по модулю два с использованием нашего предпосчета:
Матрица — искомая.
Источники информации
- Gregory V. Bard — Accelerating Cryptanalysis with the Method of Four Russians. July 22, 2006. Страница 5