Равномерная сходимость функционального ряда — различия между версиями
Baev.dm (обсуждение | вклад) (→Критерий Коши равномерной сходимости) |
(→Признак Абеля-Дирихле) |
||
| (не показано 9 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | [[Определение функционального ряда|<<]] | + | [[Определение функционального ряда|<<]] [[Операции анализа с функциональными рядами|>>]] |
== Поточечная сходимость == | == Поточечная сходимость == | ||
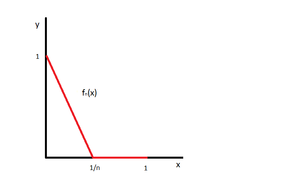
То, как была определена сумма функционального ряда, не учитывает то, что функция {{---}} закон | То, как была определена сумма функционального ряда, не учитывает то, что функция {{---}} закон | ||
| Строка 14: | Строка 14: | ||
0, & x \in (\frac1n; 1]\\ | 0, & x \in (\frac1n; 1]\\ | ||
\end{cases}</tex> | \end{cases}</tex> | ||
| + | |||
| + | [[file:picture1.png|300px]] | ||
Все <tex>f_n</tex> непрерывны на <tex>[0; 1]</tex>. <tex>f_n(0) = 1 \to 1</tex>, <tex>f(0) = 1</tex>. | Все <tex>f_n</tex> непрерывны на <tex>[0; 1]</tex>. <tex>f_n(0) = 1 \to 1</tex>, <tex>f(0) = 1</tex>. | ||
| Строка 74: | Строка 76: | ||
Как и в первой половине доказательства, | Как и в первой половине доказательства, | ||
| − | <tex>|S_m(x) - S_{n - 1}(x)| \leq \varepsilon</tex>, но <tex>S_p(x) \to S(x)</tex>. В неравенстве с <tex>\varepsilon | + | <tex>|S_m(x) - S_{n - 1}(x)| \leq \varepsilon</tex>, но <tex>S_p(x) \to S(x)</tex>. В неравенстве с <tex>\varepsilon</tex> |
можно подставлять любой фиксированный <tex>x</tex>. Устремим <tex>m \to \infty</tex>: <tex>\forall n > N\ \forall x \in E : |S_n(x) - S(x)| \leq \varepsilon</tex> | можно подставлять любой фиксированный <tex>x</tex>. Устремим <tex>m \to \infty</tex>: <tex>\forall n > N\ \forall x \in E : |S_n(x) - S(x)| \leq \varepsilon</tex> | ||
| Строка 92: | Строка 94: | ||
|author=Вейерштрасс | |author=Вейерштрасс | ||
|statement= | |statement= | ||
| − | <tex>\sum\limits_{n = 1}^\infty f_n</tex>, <tex>\forall x \in E : |f_n(x)| \leq a_n</tex>, <tex>\sum\limits_{n = 1}^\infty a_n</tex> {{---}} сходится. | + | <tex>\sum\limits_{n = 1}^\infty f_n</tex>, <tex>\forall n \in \mathbb{N} </tex> , <tex> \forall x \in E : |f_n(x)| \leq a_n</tex>, <tex>\sum\limits_{n = 1}^\infty a_n</tex> {{---}} сходится. |
Тогда <tex>\sum\limits_{n = 1}^\infty f_n</tex> равномерно сходится на <tex>E</tex>. | Тогда <tex>\sum\limits_{n = 1}^\infty f_n</tex> равномерно сходится на <tex>E</tex>. | ||
|proof= | |proof= | ||
| Строка 104: | Строка 106: | ||
<tex>\left|\sum\limits_{k = n}^m f_k(x)\right| < \varepsilon</tex>. Тогда, по критерию Коши, ряд равномерно сходится. | <tex>\left|\sum\limits_{k = n}^m f_k(x)\right| < \varepsilon</tex>. Тогда, по критерию Коши, ряд равномерно сходится. | ||
| + | }} | ||
| + | == Признак Абеля-Дирихле == | ||
| + | {{Теорема | ||
| + | |author=Абель-Дирихле | ||
| + | |statement=Для равномерной сходимости на множестве <tex>E</tex> ряда <tex>\sum\limits_{n = 1}^\infty a_n(x) b_n(x)</tex> , <tex> a_n:E \to \mathbb C</tex> и <tex> b_n:E \to \mathbb R</tex> достаточно, чтобы выполнялась пара условий <tex> \forall x \in E </tex>: | ||
| + | |||
| + | 1)Частичные суммы <tex> S_k(x)= \sum\limits_{n = 1}^k a_n(x) </tex> ряда <tex>\sum\limits_{n = 1}^\infty a_n(x) </tex> равномерно ограничены на <tex>E</tex>; | ||
| + | |||
| + | 2)Последовательность функций <tex>b_n(x)</tex> монотонна и равномерно сходится к нулю на <tex>E</tex>. | ||
| + | |||
| + | |proof= | ||
| + | |||
| + | Монотонность последовательности <tex>b_n(x)</tex> позволяет при каждом <tex>x \in E</tex> записать оценку: | ||
| + | |||
| + | <tex> |\sum\limits_{k = n}^m a_k(x) b_k(x)| \leq 4 max |A_k(x)| * max( |b_n(x)|, |b_m(x)| )</tex> | ||
| + | |||
| + | где <tex> n - 1 \leq k \leq m </tex> и в качестве <tex> A_k(x)</tex> возьмем <tex> S_k(x) - S_{n-1}(x) </tex> . | ||
| + | |||
| + | Если выполнена пара условий 1) и 2), то с одной стороны существует такая постоянная <tex>M</tex>,что <tex>|A_k(x)| \leq M</tex> при любом <tex> k \in N </tex> и любом <tex>x \in E</tex>, а с другой стороны, какого бы ни было число <tex>\varepsilon > 0 </tex>, при всех достаточно больших значениях <tex>m</tex> и <tex>n</tex> и любом <tex> x\in E</tex> будет выполнено неравенство <tex> max( |b_n(x)|, |b_m(x)| ) < \frac{\varepsilon}{4M} </tex>. Значит, что при всех достаточно больших значениях <tex>m</tex> и <tex>n</tex> и любом <tex> x \in E </tex> будет <tex>|\sum\limits_{k = n}^m a_k(x) b_k(x)| < \varepsilon </tex>, т.е. для рассматриваемого ряда выполнен критерий Коши равномерной сходимости. | ||
}} | }} | ||
| − | [[Операции анализа с функциональными рядами|>>]] | + | [[Определение функционального ряда|<<]] [[Операции анализа с функциональными рядами|>>]] |
[[Категория:Математический анализ 1 курс]] | [[Категория:Математический анализ 1 курс]] | ||
Версия 15:12, 28 ноября 2019
Содержание
Поточечная сходимость
То, как была определена сумма функционального ряда, не учитывает то, что функция — закон соответствия, который каждому сопоставляет некоторое число. При этом, все фигурировали изолированно.
Пусть на обладает свойством (например, непрерывность на ). И пусть для любого есть предел соответствующей числовой последовательности. Возникает вопрос: "Будет ли обладать свойством ?"
Приведем пример, показывающий, что если требовать лишь поточечной сходимости, то для свойство может отсутствовать.
Все непрерывны на . , .
: . Тогда, начиная с некоторого , все
Тогда будет разрывна в нуле, свойство непрерывности не сохранилось.
Равномерная сходимость
Возникает вопрос: "Что ещё надо потребовать от поточечной сходимости, чтобы в пределе сохранилось?"
Классическое требование: равномерная сходимость.
| Определение: |
| равномерно сходится к , если
Пишут, что . |
| Определение: |
| Пусть на задан функциональный ряд . Тогда он равномерно сходится к
, если |
Далее всё будем писать на языке функциональных рядов, так как их наиболее удобно использовать в
математическом анализе, и вообще это очень круто и популярно.
Критерий Коши равномерной сходимости
| Теорема (Критерий Коши равномерной сходимости): |
Ряд равномерно сходится на |
| Доказательство: |
|
Пусть ряд равномерно сходится.
, где — сумма ряда. Тогда
По определению равномерной сходимости, .
В силу предыдущего неравенства, , то есть, выполняется условие критерия Коши.
для выполняется критерий Коши сходимости числовых рядов. Значит, этот ряд сходится. На всем определена его сумма. Осталось установить равномерную сходимость ряда. По условию критерия Коши, Как и в первой половине доказательства, , но . В неравенстве с можно подставлять любой фиксированный . Устремим : Значит, определение равномерной сходимости проверено. |
Признак Вейерштрасса
Существует простой признак для проверки равномерной сходимости (признак Вейерштрасса)
Можно рассматривать и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.
| Теорема (Вейерштрасс): |
, , , — сходится.
Тогда равномерно сходится на . |
| Доказательство: |
|
Применим критерий Коши:
Сопоставляя с предыдущим неравенством, которое верно , . Тогда, по критерию Коши, ряд равномерно сходится. |
Признак Абеля-Дирихле
| Теорема (Абель-Дирихле): |
Для равномерной сходимости на множестве ряда , и достаточно, чтобы выполнялась пара условий :
1)Частичные суммы ряда равномерно ограничены на ; 2)Последовательность функций монотонна и равномерно сходится к нулю на . |
| Доказательство: |
|
Монотонность последовательности позволяет при каждом записать оценку:
где и в качестве возьмем . Если выполнена пара условий 1) и 2), то с одной стороны существует такая постоянная ,что при любом и любом , а с другой стороны, какого бы ни было число , при всех достаточно больших значениях и и любом будет выполнено неравенство . Значит, что при всех достаточно больших значениях и и любом будет , т.е. для рассматриваемого ряда выполнен критерий Коши равномерной сходимости. |