Участник:Mikhirurg/Арифметическое кодирование - дополнение — различия между версиями
Mikhirurg (обсуждение | вклад) (→Оценка минимальной и максимальной длины кода) |
(→Оценка минимальной и максимальной длины кода) |
||
| (не показаны 3 промежуточные версии 1 участника) | |||
| Строка 204: | Строка 204: | ||
На вход алгоритму передаётся последовательность символов и алфавит. Каждому символу алфавита <tex>\alpha \in \sum</tex> сопоставляется его вес <tex>w_\alpha</tex>. В начале работы алгоритма все веса символов равны <tex>1</tex>. | На вход алгоритму передаётся последовательность символов и алфавит. Каждому символу алфавита <tex>\alpha \in \sum</tex> сопоставляется его вес <tex>w_\alpha</tex>. В начале работы алгоритма все веса символов равны <tex>1</tex>. | ||
| − | Вероятность каждого символа <tex>\alpha</tex> {{---}} <tex>p(\alpha)</tex> устанавливется равной его весу, делённому на суммарный вес всех символов: <tex dpi="180">p(\alpha) = \ | + | Вероятность каждого символа <tex>\alpha</tex> {{---}} <tex>p(\alpha)</tex> устанавливется равной его весу, делённому на суммарный вес всех символов: <tex dpi="180">p(\alpha) = \dfrac{w_\alpha}{\sum_{i=1}^n w_i}</tex>. После получения очередного символа и построения нужного интервала, вес символа увеличивается на <tex>1</tex>. Когда все символы последовательности будут обработаны, необходимо либо записать маркер конца последовательности, либо запомнить её длину, чтобы позже передать декодировщику. После получения нужных границ <tex>[l, r]</tex>, в котором будет лежать код, необходмо выбрать число <tex>x</tex>, описывающее кодирование: |
| − | <tex>x \in [l, r]</tex>. Выбор числа <tex>x</tex> производится также, как и в неадаптивном алгоритме. Выбирается число вида <tex>\ | + | <tex>x \in [l, r]</tex>. Выбор числа <tex>x</tex> производится также, как и в неадаптивном алгоритме. Выбирается число вида <tex>\dfrac{x}{2^p}: x,p \in \mathbb N</tex>. |
=== Псевдокод алгоритма === | === Псевдокод алгоритма === | ||
| Строка 351: | Строка 351: | ||
L_{min} = \dfrac{1}{{\binom{l}{n+l-1}}l!} = \dfrac{1}{C_{n+l-1}^{l}l!} | L_{min} = \dfrac{1}{{\binom{l}{n+l-1}}l!} = \dfrac{1}{C_{n+l-1}^{l}l!} | ||
</tex> | </tex> | ||
| − | ==== | + | ==== Верхняя граница ==== |
Для того, чтобы максимизировать произведение, необходимо увеличить числитель каждого члена произведения. Этого можно достичь, если передать на вход алгоритму строку, состоящую из одинаковых символов. В таком случае, на каждом из шагов <tex>k=1, 2, \dots, l</tex> вес символа будет равен k, а значение кода будет изменяться в <tex>\dfrac{k}{n+k-1}</tex> раз. | Для того, чтобы максимизировать произведение, необходимо увеличить числитель каждого члена произведения. Этого можно достичь, если передать на вход алгоритму строку, состоящую из одинаковых символов. В таком случае, на каждом из шагов <tex>k=1, 2, \dots, l</tex> вес символа будет равен k, а значение кода будет изменяться в <tex>\dfrac{k}{n+k-1}</tex> раз. | ||
| Строка 367: | Строка 367: | ||
</tex> | </tex> | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |id = th1. | ||
| + | |statement=При адаптивном арифметическом кодировании строки длины <tex>l</tex>, символы которой принадлежат алфавиту мощности <tex>n</tex>, количество бит, необходимых для кодирования сообщения будет лежать в диапазоне <tex>[-\sum_{i=1}^{l} log_2{\dfrac{1}{n+i-1}}, -\sum_{i=0}^{l-1}log_2\dfrac{i+1}{n+i}]</tex> | ||
| + | |proof= | ||
| + | Произведём оценку количества бит, необходимых для записи кода $L$ в общем случае: | ||
| + | |||
| + | <tex> | ||
| + | log_2 L = -\sum_{i=1}^{l} log_2 \frac{w_{\alpha_i}}{n+i-1} | ||
| + | </tex> | ||
| + | |||
| + | Все коды лежат в диапазоне <tex>[0, 1)</tex>. | ||
| + | |||
| + | Таким образом: | ||
| + | |||
| + | Максимальное количество бит будет затрачено при записи кода, являющегося минимальной дробью: | ||
| + | |||
| + | <tex> | ||
| + | log_2 L_{min} = -\sum_{i=1}^{l} log_2 \frac{1}{n+i-1} | ||
| + | </tex> | ||
| + | |||
| + | Минимальное число бит будет затрачено в случае записи кода максимального размера: | ||
| + | |||
| + | <tex> | ||
| + | log_2 L_{max} = -\sum_{i=0}^{l-1} log_2 \frac{i+1}{n+i} | ||
| + | </tex> | ||
}} | }} | ||
Текущая версия на 16:24, 5 апреля 2020
| Определение: |
| Арифметическое кодирование (англ. Arithmetic coding) — алгоритм сжатия информации без потерь, который при кодировании ставит в соответствие тексту вещественное число из отрезка . Данный метод, как и алгоритм Хаффмана, является энтропийным, то есть длина кода конкретного символа зависит от частоты встречаемости этого символа в тексте. Арифметическое кодирование показывает более высокие результаты сжатия, чем алгоритм Хаффмана, для данных с неравномерными распределениями вероятностей кодируемых символов. |
Содержание
Принцип действия
При арифметическом кодировании каждый символ кодируется нецелым числом бит, что эффективнее кода Хаффмана (теоретически, символу с вероятностью появления допустимо ставить в соответствие код длины , следовательно, при кодировании алгоритмом Хаффмана это достигается только с вероятностями, равными обратным степеням двойки).
Кодирование
На вход алгоритму передаются текст для кодирования и список частот встречаемости символов.
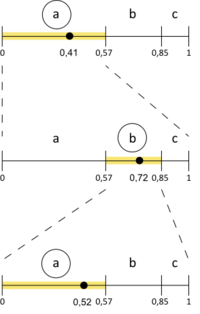
- Рассмотрим отрезок на координатной прямой.
- Поставим каждому символу текста в соответствие отрезок, длина которого равна частоте его появления.
- Считаем символ из входного потока и рассмотрим отрезок, соответствующий этому символу. Разделим этот отрезок на части, пропорциональные частотам встречаемости символов.
- Повторим пункт до конца входного потока.
- Выберем любое число из получившегося отрезка, которое и будет результатом арифметического кодирования.
Псевдокод
- — текст, подаваемый на вход;
- — длина исходного текста;
- — мощность алфавита исходного текста;
- — массив символов, составляющих алфавит исходного текста;
- — массив вероятностей обнаружения символа в тексте;
- — структура, задающая подотрезок отрезка , соответствующего конкретному символу на основе частотного анализа. Имеет поля:
- — левая граница подотрезка;
- — правая граница подотрезка;
- , — границы отрезка, содержащего возможный результат арифметического кодирования.
struct Segment:
double left
double right
Segment[m] defineSegments(letters: char[m], probability: double[m]):
Segment[m] segment
double l = 0
for i = 0 to m - 1
segment[letters[i]].left = l
segment[letters[i]].right = l + probability[i]
l = segment[letters[i]].right
return segment
double arithmeticCoding(letters: char[m], probability: double[m], s: char[n]):
Segment[m] segment = defineSegments(letters, probability)
double left = 0
double right = 1
for i = 0 to n - 1
char symb = s[i]
double newRight = left + (right - left) * segment[symb].right
double newLeft = left + (right - left) * segment[symb].left
left = newLeft
right = newRight
return (left + right) / 2
Замечание: для оптимизации размера кода можно выбрать из полученного на последнем шаге диапазона число, содержащее наименьшее количество знаков в двоичной записи.
Декодирование
Алгоритм по вещественному числу восстанавливает исходный текст.
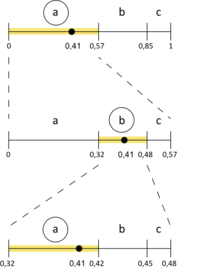
- Выберем на отрезке , разделенном на части, длины которых равны вероятностям появления символов в тексте, подотрезок, содержащий входное вещественное число. Символ, соответствующий этому подотрезку, дописываем в ответ.
- Нормируем подотрезок и вещественное число.
- Повторим пункты — до тех пор, пока не получим ответ.
Псевдокод
- — вещественное число, подаваемое на вход;
- — длина восстанавливаемого текста;
- — мощность алфавита исходного текста;
- — массив символов, составляющих алфавит исходного текста;
- — массив вероятностей обнаружения символа в тексте;
- — структура, задающая подотрезок отрезка , соответствующего конкретному символу на основе частотного анализа. Имеет поля:
- — левая граница подотрезка;
- — правая граница подотрезка;
- — значение символа.
struct Segment:
double left
double right
char character
Segment[m] defineSegments(letters: char[n], probability: double[n]):
Segment[m] segment
double l = 0
for i = 0 to m - 1
segment[i].left = l
segment[i].right = l + probability[i]
segment[i].character = letters[i]
l = segment[i].right
return segment
string arithmeticDecoding(letters: char[m], probability: double[m], code: double, n: int):
Segment[m] segment = defineSegments(letters, probability)
string s = ""
for i = 0 to n - 1
for j = 0 to m - 1
if codesegment[j].left and code < segment[j].right
s += segment[j].character
code = (code – segment[j].left) / (segment[j].right – segment[j].left)
break
return s
Замечание: кодировщику и декодировщику должно быть известно, когда завершать работу. Для этого можно передавать в качестве аргумента длину текста или символ конца файла, после которого процесс должен быть остановлен.
Замечание: Несмотря на преимущества арифметического кодирования, существует проблема при его практическом применении из-за несовершенства представления чисел с плавающей точкой в памяти компьютера — поскольку некоторые дробные числа не могут быть точно представлены в двоичном коде, используемом современными процессорами (например, ), границы символов будут округлены, что может повлечь за собой неверную работу алгоритма при больших объёмах данных. В общем случае, алгоритм можно модифицировать так, чтобы результатом было дробное число. В такой реализации вероятность встречи символа представляется в виде рационального числа. Поскольку в каждой итерации будет переход из текущего отрезка в один из его подотрезков, кратных по длине , а всего итераций , в конечном результате знаменатель дроби не превысит , а поскольку сумма всех вероятностей встречи символов равна , полученная дробь будет находиться в промежутке .
Пример работы
Рассмотрим в качестве примера строку :
Кодирование
| Символ | Частота появления |
|---|---|
| |
| |
|
| Считанный символ | Левая граница отрезка | Правая граница отрезка |
|---|---|---|
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
Код:
Декодирование
Код:
| Декодируемый символ | Код |
|---|---|
| |
| |
| |
| |
| |
| |
|
Замечание: при декодировании текста можно не только нормализовывать рабочий отрезок и текущий код, но и уменьшать рабочий отрезок (аналогично кодированию), не изменяя значение кода.
Декодирование (второй способ)
Код:
| Декодируемый символ | Границы отрезка | |||
|---|---|---|---|---|
| ||||
| ||||
| ||||
| ||||
| ||||
| ||||
| ||||
Оценка длины кодового слова
| Теорема: |
При арифметическом кодировании длина кодового слова не превышает энтропии исходного текста. |
| Доказательство: |
|
Введём следующие обозначения:
Размер сообщения можно найти по формуле: Число бит в закодированном тексте: |
Адаптивное арифметическое кодирование
Необходимость применения адаптивного алгоритма возникает в том случае, если вероятностные оценки символов сообщения не известны до начала работы алгоритма. Преимущество такого подхода кодирования заключается в том, что декодировщику не нужно передавать вероятностные оценки для символов, он будет строить их по мере декодирования сообщения, что может сильно сократить вес такого сообщения.
Алгоритм кодирования
На вход алгоритму передаётся последовательность символов и алфавит. Каждому символу алфавита сопоставляется его вес . В начале работы алгоритма все веса символов равны . Вероятность каждого символа — устанавливется равной его весу, делённому на суммарный вес всех символов: . После получения очередного символа и построения нужного интервала, вес символа увеличивается на . Когда все символы последовательности будут обработаны, необходимо либо записать маркер конца последовательности, либо запомнить её длину, чтобы позже передать декодировщику. После получения нужных границ , в котором будет лежать код, необходмо выбрать число , описывающее кодирование: . Выбор числа производится также, как и в неадаптивном алгоритме. Выбирается число вида .
Псевдокод алгоритма
- — текст, подаваемый на вход
- — длина исходного текста
- — структура, задающая подотрезок отрезка , соответствующая конкретному символу. Имеет следующие поля:
- — левая граница подотрезка
- — правая граница подотрезка
- — мощность алфавита
- — веса символов алфавита
- — набор подотрезков, соответствующих символам алфавита
- — границы отрезка, содержащие возможный результат арифметического кодирования
- — функция возвращает множество различных символов в тексте
Подотрезок
struct Segment:
double left;
double right;
Определение начальных границ подотрезков
map<char, Segment> defineSegments(set<char> alphabet):
// определяем размер подотрезков
double p = 1 / alphabet.size()
Segments[m] segments
// задаём левую и правую границы каждого из отрезков
double curLeft = 0
double curRight = p
// разбиваем отрезок [0,1) на подотрезки, соответсвующие символам алфавита
for i = 0 to m - 1
segments[i].left = curLeft
segments[i].right = curRight
curLeft = curRight
curRight = curRight + p
return segments
Перестройка подотрезков
map<char, Segment> resizeSegments(alphabet : char[m], weight : map<char, int>, segments : map<char, Segment>)
// новая левая граница подотрезка
double l = 0
// сумма весов символов алфавита
int sum = 0
// подсчет суммы весов символов алфавита
for i = 0 to m - 1
sum = sum + weight[i]
// перестроение подотрезков, для символов алфавита
for i = 0 to m - 1
char c = alphabet[i]
segments[c].left = l
segments[c].right = l + (weight[c] / sum)
l = segments[c].right;
return segments
Определение начальных весов символов алфавита
map<char, int> defineWeights(alphabet : set<char>):
map<char, int> weight
// проход по всем символам алфавита и установка начального веса
for i = 0 to m - 1
char c = alphabet[i]
weight[c] = 1
return weight
Кодирование строки
double adaptiveCoding(in : char[n], alphabet : set<char>):
int[m] weight = defineWeights(alphabet)
int[m] segments = defineSegments(alphabet)
// начальные границы отрезка
double left = 0
double right = 1
for i = 0 to n - 1
char c = in[i]
// увеличение веса символа строки
weight[c]++
// определение новых границ диапазона с искомым кодом, с учётом полученного символа c
double newRight = left + (right - left) * segments[c].right
double newLeft = left + (right - left) * segments[c].left
left = newLeft
right = newRight
resizeSegments(alphabet, weight, segments)
return (left + right) / 2;
Алгоритм декодирования
При декодировании последовательности символов также используется множество весов символов алфавита . В начале работы алгоритма все веса символов равны . На каждом шаге определяется интевал, содержащий данный код, по интервалу находится символ, который потом записывается в выходную последовательность. Вес полученного символа увеличивается на . Отрезки, соответствующие символам алфавита, перестраиваются в зависимости от изменённых весов символов и размера текущего подотрезка. При получении символа конца последовательности или обработки нужного числа символов алгоритм завершает работу.
Декодирование
- — вещественное число, подаваемое на вход;
- — длина декодируемой строки;
- — мощность алфавита;
- — веса символов алфавита;
- — веса символов алфавита;
string decode(code : double, alphabet : set<char>, int len):
map<char, int> weight = defineWeights(alphabet)
map<char, Segment> segments = defineSegments(alphabet)
string ans = ""
// декодирование строки
for i = 0 to n - 1:
// поиск нужного символа исходной строки по текущему значению кода
for j = 0 to m - 1:
char c = alphabet[j]
if code >= segments[c].left and code < segments[c].right
ans = ans + c
weight[c]++
// вычисление следующего значения кода, с учетом декодированного символа c
code = (code - segments[c].left) / segments[c].right - segments[c].left)
// перестроение подотрезков, с учётом декодированного символа c
resizeSegments(alphabet, weight, segments)
break;
return ans
Оценка минимальной и максимальной длины кода
| Теорема: |
При адаптивном арифметическом кодировании строки длины , символы которой принадлежат алфавиту мощности , полученный код будет лежать в диапазоне |
| Доказательство: |
|
Во время кодирования строки алгоритм выбирает необходимый подотрезок, увеличивает вес символа и перестраивает подотрезки. Пусть — результат кодирования строки длины , использующей алфавит длины . Код формируется следующим образом: на каждом из шагов он изменяется в раз. На каждом шаге -й символ будет иметь вес (каждый раз больший на , потому что алгоритм адаптивный). Значит, на каждом шаге суммарный вес символов будет увеличиваться на , т.е. на шаге суммарный вес символов будет равен Во время перестроения подотрезков, по алгоритму, каждому символу ствавится в соответствие подотрезок длины . В общем виде его можно представить так:
Знаменатель каждого следующего члена произведения будет увеличиваться на , так как на каждом шаге увеличивается вес одного из символов алфавита. Соответственно, чтобы минимизировать произведение, необходимо минимизировать числители его членов. Этого можно достичь, если передать на вход алгоритму строку, состоящую из неповторяющихся символов. В таком случае вес каждого из полученных символов будет равен , а значение кода на каждом из шагов будет изменяться в раз. Соответственно, формула примет вид:
Можно записать, используя формулы комбинаторики:
Верхняя границаДля того, чтобы максимизировать произведение, необходимо увеличить числитель каждого члена произведения. Этого можно достичь, если передать на вход алгоритму строку, состоящую из одинаковых символов. В таком случае, на каждом из шагов вес символа будет равен k, а значение кода будет изменяться в раз. Соответственно, формула будет иметь следующий вид:
Можно записать, используя формулы комбинаторики: |
| Утверждение: |
При адаптивном арифметическом кодировании строки длины , символы которой принадлежат алфавиту мощности , количество бит, необходимых для кодирования сообщения будет лежать в диапазоне |
|
Произведём оценку количества бит, необходимых для записи кода $L$ в общем случае:
Все коды лежат в диапазоне . Таким образом: Максимальное количество бит будет затрачено при записи кода, являющегося минимальной дробью:
Минимальное число бит будет затрачено в случае записи кода максимального размера: |