Обсуждение:Метод производящих функций — различия между версиями
Zevgeniy (обсуждение | вклад) м (UI) |
|||
| (не показаны 133 промежуточные версии 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | = | + | В комбинаторике, особенно в аналитической комбинаторике, [https://en.wikipedia.org/wiki/Symbolic_method_(combinatorics) символьный метод] - это метод подсчета [https://neerc.ifmo.ru/wiki/index.php?title=Комбинаторные_объекты комбинаторных объектов]. Он использует внутреннюю структуру объектов для получения формул их [[Производящая функция|производящих функций]]. Этот метод в основном связан с [https://en.wikipedia.org/wiki/Philippe_Flajolet Филиппом Флайоле] и подробно описан в части A его книги с [https://ru.wikipedia.org/wiki/Седжвик,_Роберт Робертом Седжвиком] "Аналитическая комбинаторика"<ref>[https://en.wikipedia.org/wiki/Analytic_Combinatorics "Аналитическая комбинаторика"]</ref>. |
| − | |||
| − | + | ==Базовые определения== | |
| − | + | Каждый комбинаторный объект состоит из атомов. | |
| − | <tex dpi="130">w | + | У атомов определен вес <tex dpi="130">w</tex>. Вес объектов равен сумме весов составляющих его атомов. |
{{Определение | {{Определение | ||
| Строка 14: | Строка 13: | ||
}} | }} | ||
| − | Производящую функцию класса <tex dpi="130">A</tex> обозначим <tex dpi="130">A(t)=\sum_{i=0}^{\infty }a_i t^i</tex>. | + | Обозначим <tex dpi="350">[t_n]</tex> как оператор взятия <tex dpi="350">n</tex>-того коэффициента производящей функции. |
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Комбинаторным классом <tex dpi="130">A</tex> называется множество комбинаторных объектов, обладающих каким-то свойством. | ||
| + | }} | ||
| + | |||
| + | =Непомеченные комбинаторные объекты= | ||
| + | |||
| + | Введём атомы <tex dpi="350">\bullet</tex> и <tex dpi="350">\circ</tex> следующим образом: | ||
| + | |||
| + | <tex dpi="130">w(\bullet)=1</tex> | ||
| + | |||
| + | <tex dpi="130">w(\circ)=0</tex> | ||
| + | |||
| + | Производящую функцию класса <tex dpi="130">A</tex> обозначим <tex dpi="130">A(t)=\sum_{i=0}^{\infty }a_i t^i</tex>, если <tex dpi="350">\{a_i\}</tex> {{---}} считающая последовательность этого класса. | ||
{{Определение | {{Определение | ||
| Строка 24: | Строка 38: | ||
Считающая последовательность: <tex dpi="130">\left \{ 0, 1, 0, ..., 0 \right \}</tex>. | Считающая последовательность: <tex dpi="130">\left \{ 0, 1, 0, ..., 0 \right \}</tex>. | ||
| − | |||
Производящая функция последовательности: <tex dpi="130">Z(t)=t</tex>. | Производящая функция последовательности: <tex dpi="130">Z(t)=t</tex>. | ||
| Строка 36: | Строка 49: | ||
Считающая последовательность: <tex dpi="130">\left \{ 1, 0, ..., 0 \right \}</tex>. | Считающая последовательность: <tex dpi="130">\left \{ 1, 0, ..., 0 \right \}</tex>. | ||
| − | |||
Производящая функция последовательности: <tex dpi="130">\varepsilon(t)=1</tex>. | Производящая функция последовательности: <tex dpi="130">\varepsilon(t)=1</tex>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Объединение комбинаторных классов== | ==Объединение комбинаторных классов== | ||
| Строка 49: | Строка 56: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Объединением комбинаторных классов <tex dpi="350">A</tex> и <tex dpi="350">B</tex> называется комбинаторный класс <tex dpi="350">C=A \cup B=A+B | + | Объединением комбинаторных классов <tex dpi="350">A</tex> и <tex dpi="350">B</tex> называется комбинаторный класс <tex dpi="350">C=A \cup B=A+B</tex>, состоящий из элементов обоих классов, причем равные объекты разных классов объявляются разными. |
}} | }} | ||
| − | + | Целью этого уточнения является возможность работать только со считающими последовательностями и производящими функциями. | |
| − | |||
<tex dpi="350">c_n=a_n+b_n</tex> | <tex dpi="350">c_n=a_n+b_n</tex> | ||
| − | <tex dpi="350">C(t)=A(t)+B(t)</tex> | + | <tex dpi="350">C(t)=\left ( \sum_{i=0}^{\infty}a_i \cdot t^i \right ) + \left ( \sum_{i=0}^{\infty}b_i \cdot t^i \right ) = \sum_{i=0}^{\infty}(a_i + b_i)\cdot t^i =A(t)+B(t)</tex> |
| − | |||
==Пары комбинаторных классов (декартово произведение комбинаторных классов)== | ==Пары комбинаторных классов (декартово произведение комбинаторных классов)== | ||
| Строка 71: | Строка 76: | ||
{{Утверждение | {{Утверждение | ||
| − | |statement=<tex dpi="350">C(t)=A(t) \cdot B(t)</tex> | + | |statement=<tex dpi="350">C(t)=A(t) \cdot B(t)</tex><ref>[[Арифметические действия с формальными степенными рядами]]</ref> |
| − | |||
}} | }} | ||
==Последовательности комбинаторных классов== | ==Последовательности комбинаторных классов== | ||
| + | |||
| + | ===Ограниченная конструкция=== | ||
{{Определение | {{Определение | ||
| Строка 93: | Строка 99: | ||
'''Переход'''. | '''Переход'''. | ||
| − | :Пусть для <tex dpi="350">k=n</tex> верно <tex dpi="350">Seq_n(A)(t)=A(t)^n</tex>. Докажем для | + | :Пусть для <tex dpi="350">k=n</tex> верно <tex dpi="350">Seq_n(A)(t)=A(t)^n</tex>. Докажем для <tex dpi="350">k=n+1</tex>: |
| − | <tex dpi="350">k=n+1</tex>: <tex dpi="350">Seq_{n+1}(A)(t)=A(t)^{n+1}</tex>. Рассмотрим <tex dpi="350">Seq_{n+1}(A)</tex> как <tex dpi="350">Pair(Seq_n(A), A)</tex>. Тогда <tex dpi="350">Seq_{n+1}(A)(t)=A(t)^n \cdot A(t)=A(t)^{n+1}</tex>. | + | <tex dpi="350">Seq_{n+1}(A)(t)=A(t)^{n+1}</tex>. Рассмотрим <tex dpi="350">Seq_{n+1}(A)</tex> как <tex dpi="350">Pair(Seq_n(A), A)</tex>. Тогда <tex dpi="350">Seq_{n+1}(A)(t)=A(t)^n \cdot A(t)=A(t)^{n+1}</tex>. |
}} | }} | ||
| − | + | ===Неограниченная конструкция=== | |
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Последовательностью | + | Последовательностью объектов из <tex dpi="350">A</tex> называется <tex dpi="350">B=Seq(A)=\sum_{i=0}^{\infty}Seq_i(A)</tex>. |
}} | }} | ||
| Строка 111: | Строка 117: | ||
| − | '''Ограничение:''' <tex dpi="350">a_0=0</tex>. Этому есть как техническое, так и комбинаторное объяснение. | + | '''Ограничение:''' <tex dpi="350">a_0=0</tex> (также можно встретить <tex dpi="350">A_0=0</tex>). Этому есть как техническое, так и комбинаторное объяснение. |
* Технически, если <tex dpi="350">a_0>1</tex>, то мы будем делить на отрицательное число; если <tex dpi="350">a_0=1</tex>, то на функцию, у которой свободный член <tex dpi="350">0</tex>, {{---}} что формализм производящих функций сделать не позволяет. | * Технически, если <tex dpi="350">a_0>1</tex>, то мы будем делить на отрицательное число; если <tex dpi="350">a_0=1</tex>, то на функцию, у которой свободный член <tex dpi="350">0</tex>, {{---}} что формализм производящих функций сделать не позволяет. | ||
* Комбинаторное объяснение заключается в том, что если объектов веса ноль более 0, то мы можем создать бесконечное количество последовательностей веса 0 (комбинируя такие объекты), а мы хотим работать с конечными количествами последовательностей. | * Комбинаторное объяснение заключается в том, что если объектов веса ноль более 0, то мы можем создать бесконечное количество последовательностей веса 0 (комбинируя такие объекты), а мы хотим работать с конечными количествами последовательностей. | ||
| − | + | ====Примеры==== | |
| − | + | * Последовательности из не менее, чем 3 объектов: | |
| − | |||
| − | Примеры | ||
| − | * | ||
** <tex dpi="350">Seq_{\geq 3}=Pair(Seq_3(A), Seq(A))=Seq(A)-Seq_0(A)-Seq_1(A)-Seq_2(A)</tex> | ** <tex dpi="350">Seq_{\geq 3}=Pair(Seq_3(A), Seq(A))=Seq(A)-Seq_0(A)-Seq_1(A)-Seq_2(A)</tex> | ||
** <tex dpi="350">Seq_{\geq 3}(t)=Pair(Seq_3(A), Seq(A))(t)=A(t)^3 \cdot \frac{1}{1-A(t)}=\frac{A(t)^3}{1-A(t)}=(Seq(A)-Seq_0(A)-Seq_1(A)-Seq_2(A))(t)=\frac{1}{1-A(t)}-0-A(t)-A(t)^2</tex> | ** <tex dpi="350">Seq_{\geq 3}(t)=Pair(Seq_3(A), Seq(A))(t)=A(t)^3 \cdot \frac{1}{1-A(t)}=\frac{A(t)^3}{1-A(t)}=(Seq(A)-Seq_0(A)-Seq_1(A)-Seq_2(A))(t)=\frac{1}{1-A(t)}-0-A(t)-A(t)^2</tex> | ||
* Последовательности чётной длины: | * Последовательности чётной длины: | ||
** <tex dpi="350">Seq_{\vdots 2}(A)=Seq(Pair(A, A))</tex> | ** <tex dpi="350">Seq_{\vdots 2}(A)=Seq(Pair(A, A))</tex> | ||
| − | ** <tex dpi="350">Seq_{\vdots 2}(A)(t)=Seq(Pair(A, A))(t)=\frac{1}{1-A(t | + | ** <tex dpi="350">Seq_{\vdots 2}(A)(t)=Seq(Pair(A, A))(t)=\frac{1}{1-A\left (t^2\right )}</tex> |
| + | |||
| + | ==Комбинаторный класс "Натуральные числа"== | ||
| + | |||
| + | Вес числа равен его значению. Каждое натуральное число встречается 1 раз. | ||
| + | |||
| + | Считающая последовательность: <tex dpi="350">\left \{ 0, 1, ..., 1 \right \}</tex> | ||
| + | |||
| + | <tex dpi="350">w(n)=n</tex> | ||
| + | |||
| + | Класс "Натуральные числа" принято обозначать <tex dpi="350">I</tex>. | ||
| + | Считающая последовательность {{---}} | ||
| + | <tex dpi="350">c_n=\left\{\begin{matrix} | ||
| + | 0, n=0\\ | ||
| + | 1, n>0 | ||
| + | \end{matrix}\right.</tex> | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement=<tex dpi="350">I(t)=\frac{t}{1 - t}</tex> | ||
| + | |proof= | ||
| + | Производящей функцией последовательности из <tex dpi="350">1</tex> явлется <tex>Seq(\{1\})=\frac{1}{1-t}</tex>. | ||
| + | |||
| + | Чтобы получить производящую функцию класса натуральных чисел, произведем сдвиг вправо по правилам работы со степенными рядами: | ||
| + | <tex dpi="350">t \cdot I(t) = t \cdot \frac{1}{1 - t} = \frac{t}{1-t}</tex> | ||
| + | }} | ||
| + | |||
| + | ===Применение=== | ||
| − | --- | + | <tex dpi="350">Seq(I)</tex> {{---}} упорядоченное [[Нахождение количества разбиений числа на слагаемые|разбиение натуральных чисел на слагаемые]]. |
| + | Тогда производящая функция {{---}} <tex dpi="350">Seq(I)(t)=\frac{1}{1-\frac{t}{1-t}}=\frac{1-t}{1-2t}=\frac{1}{1-2t}-\frac{t}{1-2t}</tex> | ||
| − | + | <tex dpi="350">\left [ t^n \right ] \frac{1-t}{1-2t} = \left\{\begin{matrix} | |
| + | 2 ^ n - 2 ^ {n - 1} = 2 ^ {n - 1}, n > 0 | ||
| + | \\ | ||
| + | 1, n = 0 | ||
| + | \end{matrix}\right.</tex>, потому что <tex dpi="350">\frac{1}{1-2t}</tex> соответсвует ряду степеней <tex dpi="350">2</tex>, а <tex dpi="350">\frac{1}{1-2t}</tex> {{---}} ряду <tex dpi="350">2^{x-1}</tex>. | ||
| + | |||
| + | ==Множества== | ||
| + | |||
| + | {{Определение | ||
| + | |definition=Множества <tex dpi="350">Set(A)</tex> {{---}} последовательности без повторений и порядка элементов. | ||
| + | }} | ||
| + | {{Утверждение | ||
| + | |statement=<tex dpi="350">Set(A)=\prod_{\alpha \in A}\left(\varepsilon+\left \{ \alpha \right \}\right )</tex> | ||
| + | |proof=Докажем по индукции по потенциальным элементам множеств <tex dpi="350">A</tex>. | ||
| + | |||
| + | '''База''' | ||
| + | |||
| + | <tex dpi="350">A=\varnothing</tex> | ||
| + | |||
| + | <tex dpi="350">Set(\varnothing)=\varepsilon=\prod_{\alpha\in A}\varepsilon</tex> | ||
| + | |||
| + | '''Переход''' | ||
| + | |||
| + | Пусть верно для множества <tex dpi="350">A_1</tex>, докажем, что будет верно и для множества и <tex dpi="350">A_1+\{\alpha\}</tex>, где <tex dpi="350">\alpha\in A\setminus A_1</tex> | ||
| + | В множестве каждый элемент может либо присутствовать, либо отсутствовать, поэтому <tex dpi="350">Set(A_1+\{\alpha\})=Set(A_1)+Set(A_1)\times\{\alpha\}=Set(A_1)(\varepsilon + \alpha)</tex>. | ||
| + | }} | ||
| + | |||
| + | ====Пример==== | ||
| + | * <tex dpi="350">A = \left \{ \alpha, \beta, \gamma \right \}</tex> | ||
| + | * <tex dpi="350">Set(A) = \left \{ \varnothing, \left \{ \alpha \right \}, \left \{ \beta\right \}, \left \{ \gamma \right \}, \left \{ \alpha, \beta\right \}, \left \{ \alpha, \gamma \right \}, \left \{ \beta, \gamma \right \}, \left \{ \alpha, \beta, \gamma \right \} \right \}</tex> | ||
| + | |||
| + | <tex dpi="350">Set(A)(t)=\prod_{\alpha \in A}\left(\varepsilon+\left \{ \alpha \right \}\right )(t)=\prod_{\alpha \in A}(1+t^{w(\alpha)})=\prod_{n=0}^{\infty}(1+t^n)^{a_n}</tex> | ||
| + | |||
| + | ==Мультимножества== | ||
| + | |||
| + | {{Определение | ||
| + | |definition=Мультимножества <tex dpi="350">MSet(A)</tex> {{---}} последовательности с повторениями, но без порядка элементов. | ||
| + | }} | ||
| + | Как и с <tex dpi="350">Seq(A)</tex> существует ограничение на <tex dpi="350">A</tex>: <tex dpi="350">a_0=A(0)=0</tex>. | ||
| + | {{Утверждение | ||
| + | |statement=<tex dpi="350">MSet(A)=\prod_{\alpha \in A}Seq(\left \{ \alpha \right \})</tex> | ||
| + | |proof=Докажем по индукции по потенциальным элементам множеств <tex dpi="350">A</tex>. | ||
| + | |||
| + | '''База''' | ||
| + | |||
| + | <tex dpi="350">A=\varnothing</tex> | ||
| + | |||
| + | <tex dpi="350">MSet(\varnothing)=\varepsilon=\prod_{\alpha\in A}\varepsilon</tex> | ||
| + | |||
| + | '''Переход''' | ||
| + | |||
| + | Отличие от множеств в том, что здесь каждый элемент может присутствовать в любом неотрицательном количестве экземпляров, поэтому для каждого элемента <tex dpi="350">\alpha</tex> берется <tex dpi="350">Seq(\{\alpha\})</tex> | ||
| + | |||
| + | Пусть верно для мультимножества <tex dpi="350">A_1</tex>, докажем, что будет верно и для мультимножества и <tex dpi="350">A_1+Seq_{\geq1}(\{\alpha\})</tex>, где <tex dpi="350">\alpha\in A\setminus A_1</tex> | ||
| + | <tex dpi="350">MSet(A_1+\{\alpha\})=MSet(A_1)+MSet(A_1)\times\{\alpha\}\times Seq_{\geq 1}(\{\alpha \})=MSet(A_1)\cdot Seq(\{\alpha\})</tex>. | ||
| + | }} | ||
| + | |||
| + | <tex dpi="350">MSet(A)(t)=\prod_{\alpha \in A}Seq(\left \{ \alpha \right \})(t)=\prod_{\alpha \in A}\frac{1}{1-t^{w(\alpha)}}=\prod_{n=1}^{\infty}\left(\frac{1}{1-t^n}\right)^{a_n}</tex> | ||
| + | |||
| + | =Помеченные объекты= | ||
| + | |||
| + | Как можно заметить, для некоторых операторов, например, <tex dpi="350">Set</tex> и <tex dpi="350">MSet</tex> не существует замкнутых формул, поэтому их объекты удобнее обозначать как помеченные. С помеченными объектами используется [https://en.wikipedia.org/wiki/Generating_function#Exponential_generating_function_(EGF) экспоненциальная производящая функция]. | ||
| + | |||
| + | Напомним, что если <tex dpi="350">\left \{ a_i \right \}</tex> {{---}} считающая последовательность, то производящие функции выражаются следующим образом: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Обычная || <tex dpi="350">ogf(t) = \sum_{i=0}^{\infty}a_it^i</tex> | ||
| + | |- | ||
| + | | Экспоненциальная || <tex dpi="350">egf(t) = \sum_{i=0}^{\infty}\frac{a_it^i}{n!}</tex> | ||
| + | |} | ||
| + | |||
| + | Далее под производящей функцией будет подразумеваться и использоваться экспоненциальная производящая функция, потому что формулы с ней более просты в работе. | ||
| + | |||
| + | ==Свойства экспоненциальной производящей функции== | ||
{{Утверждение | {{Утверждение | ||
|statement= | |statement= | ||
| − | <tex dpi=" | + | Пусть <tex dpi="350">A(t)</tex> {{---}} экспоненциальная производящая функция последовательности <tex dpi="350">\{ a_0, a_1, ..., a_n, ... \}</tex>, тогда <tex dpi="350">A'(t)</tex> {{---}} экспоненциальная производящая функция последовательности <tex dpi="350">B=\{ a_1, a_2, ..., a_n, ... \}</tex> |
|proof= | |proof= | ||
| + | <tex dpi="350">B(t)=\sum_{n=0}^{\infty}\frac{a_{i+1}t^n}{n!}=\sum_{n=0}^{\infty}\frac{a_{i+1}t^n(n+1)}{(n+1)!}=A'(t)</tex> | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | <tex dpi="350">\left (\int A(t) \right )'=A(t)</tex><ref>[https://youtu.be/UwOjanKAMt0?list=PLrV7qfjOKnis2aCBAVcirxr_oxhNKoO6e&t=2131 Youtube {{---}} Помеченные объекты]</ref> | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | Пусть <tex dpi="350">A(t)</tex> {{---}} экспоненциальная производящая функция последовательности <tex dpi="350">\{ a_0, a_1, ..., a_n, ... \}</tex>, тогда <tex dpi="350">\int A(t)</tex> {{---}} экспоненциальная производящая функция последовательности <tex dpi="350">B=\{ 0, a_0, a_1, a_2, ..., a_n, ... \}</tex><ref>[https://youtu.be/UwOjanKAMt0?list=PLrV7qfjOKnis2aCBAVcirxr_oxhNKoO6e&t=2131 Youtube {{---}} Помеченные объекты]</ref> | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Утверждение | ||
| + | |statement=С точки зрения комбинаторики композиция производящих функций <tex dpi="350">A</tex> и <tex dpi="350">B</tex> означает подстановку вместо каждого возможного атома в <tex dpi="350">A</tex> всех объектов из класса <tex dpi="350">B</tex>. | ||
| + | |||
| + | <tex dpi="350">A \left ( B \left ( t \right ) \right )=\sum_{n=0}^{\infty}\frac{B(t)^n\cdot a_n}{n!}</tex> | ||
| + | |||
| + | <tex dpi="350">c_n=\sum_{k=0}^na_k\sum_{t_1+t_2+...+t_k=n}\binom{n}{t_1, t_2, ..., t_n}\cdot b_{t_1} b_{t_2}\cdot...\cdot b_{t_n}</tex> | ||
| + | }} | ||
| + | |||
| + | ==Помеченные объекты== | ||
| + | |||
| + | Помеченные комбинаторные объекты отличаются тем, что все атомы имеет разные значки; Если вес объекта равен <tex dpi="350">n</tex>, то все атомы пронумерованы различными целыми числами от <tex dpi="350">1</tex> до <tex dpi="350">n</tex>. | ||
| + | |||
| + | <tex dpi="130">w(①)=1</tex> | ||
| + | |||
| + | <tex dpi="130">w(\circ)=0</tex> | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Комбинаторным объектом <tex dpi="130">Z</tex> называется комбинаторный объект, состоящий из одного атома веса <tex dpi="130">1</tex>. | ||
| + | |||
| + | <tex dpi="130">Z=\left \{ ① \right \}</tex> | ||
| + | |||
| + | <tex dpi="130">Z(t)=t</tex> | ||
| + | }} | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | Комбинаторным объектом <tex dpi="130">\varepsilon</tex> называется комбинаторный объект, состоящий из одного атома веса <tex dpi="130">0</tex>. | ||
| + | |||
| + | <tex dpi="130">\varepsilon=\left \{ \circ \right \}</tex> | ||
| + | |||
| + | <tex dpi="130">\varepsilon(t)=1</tex> | ||
| + | }} | ||
| + | |||
| + | ==Объединение комбинаторных классов== | ||
| + | |||
| + | Одинаковых объектов также нет, мы ставим разные метки на одинаковые объекты из разных классов, чтобы сделать их различными. | ||
| + | |||
| + | <tex dpi="350">c_n=a_n+b_n</tex> | ||
| + | |||
| + | <tex dpi="350">C(t)=\left ( \sum_{i=0}^{\infty}\frac{a_i \cdot t^i}{i!} \right ) + \left ( \sum_{i=0}^{\infty}\frac{b_i \cdot t^i}{i!} \right ) = \sum_{i=0}^{\infty}\frac{(a_i + b_i)\cdot t^i}{i!}=A(t)+B(t)</tex> | ||
| + | |||
| + | |||
| + | ==Пары комбинаторных классов (декартово произведение комбинаторных классов)== | ||
| + | |||
| + | Декартово произведение, определенное для непомеченных объектов, нам не даст корректный комбинаторный объект. | ||
| + | |||
| + | Пусть <tex dpi="350">A= \{</tex> [[Файл:1-2.png|50px]] <tex dpi="350">\}</tex>, | ||
| + | <tex dpi="350">B= \{</tex> [[Файл:1-2-3.png|50px]] <tex dpi="350">\}</tex>. | ||
| + | |||
| + | Тогда пара <tex dpi="350">(</tex> [[Файл:1-2.png|50px]] <tex dpi="350">,</tex>[[Файл:1-2-3.png|50px]]<tex dpi="350">)</tex> будет иметь вес 5, но атомы не будут иметь различные пометки от 1 до 5. | ||
| + | |||
| + | Поэтому введем оператор <tex dpi="350">A \star B</tex>, который | ||
| + | # Перебирает все пары из <tex dpi="350">A</tex> и <tex dpi="350">B</tex>. | ||
| + | # В каждой паре перебирает все возможные способы перенумеровать атомы. Нумерация идёт в том же порядке, что и изначальная. То есть для каждого цикла при фиксированном наборе номеров есть ровно 1 способ занумеровать. Таким образом, в классе <tex dpi="350">A \star B</tex> будет лежать <tex dpi="350">(</tex> [[Файл:1-2.png|50px]] <tex dpi="350">,</tex>[[Файл:3-4-5.png|50px]]<tex dpi="350">)</tex>, но не будет лежать <tex dpi="350">(</tex> [[Файл:1-2.png|50px]] <tex dpi="350">,</tex>[[Файл:3-5-4.png|50px]]<tex dpi="350">)</tex>. | ||
| + | |||
| + | <tex dpi="350">c_n=\sum_{k=0}^na_kb_{n-k}\binom{n}{k}=\sum_{k=0}^na_kb_{n-k}\frac{n!}{k!(n-k)!}=n! \cdot \sum_{k=0}^n\frac{a_k}{k!}\frac{b_{n-k}}{(n-k)!}</tex> | ||
| + | |||
| + | <tex dpi="350">C(t)=A(t) \cdot B(t)</tex> | ||
| + | |||
| + | ==Последовательности комбинаторных классов== | ||
| + | |||
| + | ===Ограниченная конструкция=== | ||
| + | |||
| + | Последовательности длины <tex dpi="350">k</tex>, как и в непомеченных комбинаторных объектах, формируются следующим образом: | ||
| + | * Cоставляются все возможные последовательности из <tex dpi="350">k</tex> объектов из <tex dpi="350">A</tex> | ||
| + | * Перенумеруются всеми возможными способами. | ||
| + | Их принято обозначать <tex dpi="350">Seq_k(A)</tex>. | ||
| − | <tex dpi=" | + | <tex dpi="350">n</tex>-тый член выражается следующим образом: <tex dpi="350">b_n=\sum_{t_1+t_2+...+t_k=n}\binom{n}{t_1}\cdot\binom{n-t_1}{t_2}\cdot...\cdot\binom{t_k}{t_k}\cdot\prod_{i=1}^{k}a_{t_i}=\sum_{t_1+t_2+...+t_k=n}\binom{n}{t_1, t_2,...,t_k}\cdot\prod_{i=1}^{k}a_{t_i}=\sum_{t_1+t_2+...+t_k=n}\frac{n!}{t_1! \cdot t_2! \cdot ... \cdot t_k!}\cdot\prod_{i=1}^{k}a_{t_i}=n!\sum_{t_1+t_2+...+t_k=n}\prod_{i=1}^{k}\frac{a_{t_i}}{t_i!}</tex> |
| − | + | Поэтому производящая функция {{---}} <tex dpi="350">B(t)=\left ( A\left (t\right ) \right )^k</tex> | |
| − | + | ===Неограниченная конструкция=== | |
| − | |||
| − | + | Определение <tex dpi="350">Seq(A)</tex> не изменилось. | |
| − | + | ||
| + | {{Утверждение | ||
| + | |statement=<tex dpi="350">Seq(A)(t)=\frac{1}{1 - A(t)}</tex> | ||
| + | |proof=<tex dpi="350">Seq(A)(t)=\sum_{i=0}^{\infty}Seq_i(A)(t)=\sum_{i=0}^{\infty}A(t)^i=\frac{1}{1 - A(t)}</tex> (Геометрическая прогрессия) | ||
}} | }} | ||
| + | Действует ограничение на <tex dpi="350">b_0=B(0)=0</tex>, как и на <tex dpi="350">Seq(A)</tex> и <tex dpi="350">MSet(A)</tex> в формализме непомеченных объектов. | ||
| − | + | ====Пример==== | |
| − | + | '''Перестановки''' | |
| − | + | * <tex dpi="350">P=Seq(Z)</tex> | |
| − | + | * Экспоненциальной производящей функцией является <tex dpi="350">P(t)=\frac{1}{1-t}</tex>. | |
| − | + | * Обычной производящей функции <tex dpi="350">\frac{1}{1-t}</tex> соответствует считающая последовательность <tex dpi="350">\left \{ 1, 1, ..., 1\right \}</tex>, поэтому <tex dpi="350">[t_n]\frac{1}{1-t}=1</tex>. | |
| − | + | * <tex dpi="350">p_n=n!\cdot[t_n]p(t)=n!</tex> | |
| − | + | ||
| − | + | ==Урны== | |
| − | | | + | Кобинаторный класс "Урна" {{---}} множество, характеризующееся только количеством атомов в объекте, то есть элементов каждого веса {{---}} <tex dpi="350">1</tex>, поэтому <tex dpi="350">a_n=1</tex>. |
| − | + | ||
| − | + | Производящая функция этого класса {{---}} <tex dpi="350">edf(t)=\sum_{n=0}^{\infty}\frac{1\cdot t^n}{n!}=\sum_{n=0}^{\infty}\frac{t^n}{n!}=e^t</tex>. | |
| − | + | ||
| − | + | ==Множества== | |
| + | |||
| + | В формализме помеченных объектов <tex dpi="350">MSet=Set</tex>, потому что не бывает одинаковых элементов в множествах. | ||
| + | |||
| + | ===Ограниченная конструкция=== | ||
| + | |||
| + | {{Определение | ||
| + | |definition=Ограниченным множеством <tex dpi="350">A=Set_k(B)</tex> назовём множество из <tex dpi="350">k</tex> объектов (порядок не важен). | ||
| + | }} | ||
| + | |||
| + | Рассмотрим <tex dpi="350">\left \{ a_1, a_2, ..., a_k \right \} \in Set_k(B)</tex> и разобьем последовательности в <tex dpi="350">Seq_k(B)</tex> на классы эквивалентности по признаку равенства множеств элементов в них. | ||
| + | |||
| + | Каждому <tex dpi="350">Set_k(B)</tex> [[Отображения|биективно]] соответствует <tex dpi="350">k!</tex> последовательностей в <tex dpi="350">Seq_k(B)</tex>, потому что все объекты различны. | ||
| + | |||
| + | <tex dpi="350">Set_k(B)\cdot k!=Seq_k(B)</tex> | ||
| + | |||
| + | <tex dpi="350">Set_k(B)(t)=A(t)=\frac{\left ( B \left ( t \right ) \right )^k}{k!}</tex> | ||
| + | |||
| + | ===Неограниченная конструкция=== | ||
| + | |||
| + | <tex dpi="350">A=Set(B)=\sum_{k=0}^{\infty}Set_k(b)</tex> {{---}} множества объектов (порядок не важен). | ||
| + | |||
| + | Ограничение <tex dpi="350">b_0=B(0)=0</tex> также действует. | ||
| + | |||
| + | <tex dpi="350">Set(A)(t)=\sum_{k=0}^{\infty}\frac{A(t)^k}{k!}=e^{A(t)}</tex> | ||
| + | |||
| + | Можно рассматривать <tex dpi="350">Set(A)</tex> как композицию урны и <tex dpi="350">A</tex>, другими словами, можно вместо атомов в урне взять объекты класса <tex dpi="350">A</tex>. | ||
| + | |||
| + | ==Циклы== | ||
| + | |||
| + | ===Ограниченная конструкция=== | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Цикл <tex dpi="350">A=Cycle_k(B)</tex> {{---}} ориентированная циклическая последовательность из <tex dpi="350">k</tex> объектов класса <tex dpi="350">B</tex>. | ||
| + | |||
| + | Циклов нулевой длины <tex dpi="350">0</tex>, то есть, <tex dpi="350">c_0=0</tex>. | ||
| + | }} | ||
| − | + | {{Утверждение | |
| + | |statement= | ||
| + | Каждому циклу <tex dpi="350">(b_1, b_2, ..., b_k)</tex> длины <tex dpi="350">k</tex> биективно соответствует <tex dpi="350">k</tex> упорядоченных последовательностей ([https://en.wikipedia.org/wiki/Cyclic_permutation циклические перестановки] элементов цикла). | ||
| + | }} | ||
| − | + | Поэтому <tex dpi="350">Seq_k(A) = k\cdot Cycle_k(A)</tex> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Значит, экспоненциальная производящая функция циклов {{---}} <tex dpi="350">Cycle_k(A)(t)=\frac{Seq_k(A)(t)}{k}=\frac{A(t)^k}{k}</tex>. | |
| − | |||
| − | + | ===Неограниченная конструкция=== | |
| − | + | {{Определение | |
| + | |definition=Циклы <tex dpi="350">A=Cycle(B)=\sum_{k=0}^{\infty}Cycle_k(B)</tex>. | ||
| + | }} | ||
| + | <tex dpi="350">Cycle(A)(t)=\sum_{k=0}^{\infty}Cycle_k(A)(t)=0+\sum_{k=1}^{\infty}\frac{A(t)^k}{k}=-ln \left (1+\left (-A(t)\right ) \right )=-ln \left (1-A(t) \right )=ln\left (\frac{1}{1-A(t)}\right )</tex> (Разложение натурального логарифма в ряд Тейлора) | ||
| − | + | =См.также= | |
| + | *[[Конструирование комбинаторных объектов и их подсчёт]] | ||
| + | *[[Функция Эйлера]] | ||
| + | *[[Лемма Бёрнсайда и Теорема Пойа]] | ||
| + | *[[Задача об ожерельях]] | ||
| + | *[[Числа Каталана]] | ||
| + | *[[Генерация комбинаторных объектов в лексикографическом порядке]] | ||
| + | *[[Подсчет деревьев]] | ||
| − | + | =Примeчания= | |
| − | + | <references/> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | =Источники информации= | |
| + | *[https://youtu.be/J2L-vdytqC0?list=PLrV7qfjOKnis2aCBAVcirxr_oxhNKoO6e Artem Vasilyev {{---}} Descrete maths lectures, unmarked objects] | ||
| + | *[https://youtu.be/UwOjanKAMt0?list=PLrV7qfjOKnis2aCBAVcirxr_oxhNKoO6e Artem Vasilyev {{---}} Descrete maths lectures, marked objects] | ||
| + | *[https://neerc.ifmo.ru/wiki/index.php?title=Конструирование_комбинаторных_объектов_и_их_подсчёт Викиконспекты {{---}} Конструирование комбинаторных объектов и их подсчёт] | ||
| + | *[https://en.wikipedia.org/wiki/Symbolic_method_(combinatorics) Wikipedia {{---}} Symbolic method] | ||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| − | + | [[Категория: Комбинаторика]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Текущая версия на 22:29, 20 августа 2020
В комбинаторике, особенно в аналитической комбинаторике, символьный метод - это метод подсчета комбинаторных объектов. Он использует внутреннюю структуру объектов для получения формул их производящих функций. Этот метод в основном связан с Филиппом Флайоле и подробно описан в части A его книги с Робертом Седжвиком "Аналитическая комбинаторика"[1].
Содержание
- 1 Базовые определения
- 2 Непомеченные комбинаторные объекты
- 3 Помеченные объекты
- 4 См.также
- 5 Примeчания
- 6 Источники информации
Базовые определения
Каждый комбинаторный объект состоит из атомов.
У атомов определен вес . Вес объектов равен сумме весов составляющих его атомов.
| Определение: |
| Считающей последовательностью называется последовательность , где — количество объектов веса . |
Обозначим как оператор взятия -того коэффициента производящей функции.
| Определение: |
| Комбинаторным классом называется множество комбинаторных объектов, обладающих каким-то свойством. |
Непомеченные комбинаторные объекты
Введём атомы и следующим образом:
Производящую функцию класса обозначим , если — считающая последовательность этого класса.
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса . |
Считающая последовательность: .
Производящая функция последовательности: .
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса . . |
Считающая последовательность: .
Производящая функция последовательности: .
Объединение комбинаторных классов
| Определение: |
| Объединением комбинаторных классов и называется комбинаторный класс , состоящий из элементов обоих классов, причем равные объекты разных классов объявляются разными. |
Целью этого уточнения является возможность работать только со считающими последовательностями и производящими функциями.
Пары комбинаторных классов (декартово произведение комбинаторных классов)
| Определение: |
| Парой комбинаторных классов и называется комбинаторный класс . |
| Утверждение: |
Последовательности комбинаторных классов
Ограниченная конструкция
| Определение: |
| Последовательностью объектов из называется . |
| Утверждение: |
|
Докажем по индукции: База .
Переход.
|
Неограниченная конструкция
| Определение: |
| Последовательностью объектов из называется . |
| Утверждение: |
| (Геометрическая прогрессия) |
Ограничение: (также можно встретить ). Этому есть как техническое, так и комбинаторное объяснение.
- Технически, если , то мы будем делить на отрицательное число; если , то на функцию, у которой свободный член , — что формализм производящих функций сделать не позволяет.
- Комбинаторное объяснение заключается в том, что если объектов веса ноль более 0, то мы можем создать бесконечное количество последовательностей веса 0 (комбинируя такие объекты), а мы хотим работать с конечными количествами последовательностей.
Примеры
- Последовательности из не менее, чем 3 объектов:
- Последовательности чётной длины:
Комбинаторный класс "Натуральные числа"
Вес числа равен его значению. Каждое натуральное число встречается 1 раз.
Считающая последовательность:
Класс "Натуральные числа" принято обозначать . Считающая последовательность —
| Утверждение: |
|
Производящей функцией последовательности из явлется . Чтобы получить производящую функцию класса натуральных чисел, произведем сдвиг вправо по правилам работы со степенными рядами: |
Применение
— упорядоченное разбиение натуральных чисел на слагаемые.
Тогда производящая функция —
, потому что соответсвует ряду степеней , а — ряду .
Множества
| Определение: |
| Множества — последовательности без повторений и порядка элементов. |
| Утверждение: |
|
Докажем по индукции по потенциальным элементам множеств . База
Переход Пусть верно для множества , докажем, что будет верно и для множества и , где В множестве каждый элемент может либо присутствовать, либо отсутствовать, поэтому . |
Пример
Мультимножества
| Определение: |
| Мультимножества — последовательности с повторениями, но без порядка элементов. |
Как и с существует ограничение на : .
| Утверждение: |
|
Докажем по индукции по потенциальным элементам множеств . База
Переход Отличие от множеств в том, что здесь каждый элемент может присутствовать в любом неотрицательном количестве экземпляров, поэтому для каждого элемента берется Пусть верно для мультимножества , докажем, что будет верно и для мультимножества и , где . |
Помеченные объекты
Как можно заметить, для некоторых операторов, например, и не существует замкнутых формул, поэтому их объекты удобнее обозначать как помеченные. С помеченными объектами используется экспоненциальная производящая функция.
Напомним, что если — считающая последовательность, то производящие функции выражаются следующим образом:
| Обычная | |
| Экспоненциальная |
Далее под производящей функцией будет подразумеваться и использоваться экспоненциальная производящая функция, потому что формулы с ней более просты в работе.
Свойства экспоненциальной производящей функции
| Утверждение: |
Пусть — экспоненциальная производящая функция последовательности , тогда — экспоненциальная производящая функция последовательности |
| Утверждение: |
| Утверждение: |
Пусть — экспоненциальная производящая функция последовательности , тогда — экспоненциальная производящая функция последовательности [4] |
| Утверждение: |
С точки зрения комбинаторики композиция производящих функций и означает подстановку вместо каждого возможного атома в всех объектов из класса .
|
Помеченные объекты
Помеченные комбинаторные объекты отличаются тем, что все атомы имеет разные значки; Если вес объекта равен , то все атомы пронумерованы различными целыми числами от до .
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса .
|
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса .
|
Объединение комбинаторных классов
Одинаковых объектов также нет, мы ставим разные метки на одинаковые объекты из разных классов, чтобы сделать их различными.
Пары комбинаторных классов (декартово произведение комбинаторных классов)
Декартово произведение, определенное для непомеченных объектов, нам не даст корректный комбинаторный объект.
Тогда пара ![]()
![]() будет иметь вес 5, но атомы не будут иметь различные пометки от 1 до 5.
будет иметь вес 5, но атомы не будут иметь различные пометки от 1 до 5.
Поэтому введем оператор , который
- Перебирает все пары из и .
- В каждой паре перебирает все возможные способы перенумеровать атомы. Нумерация идёт в том же порядке, что и изначальная. То есть для каждого цикла при фиксированном наборе номеров есть ровно 1 способ занумеровать. Таким образом, в классе будет лежать
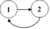
 , но не будет лежать
, но не будет лежать 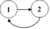
 .
.
Последовательности комбинаторных классов
Ограниченная конструкция
Последовательности длины , как и в непомеченных комбинаторных объектах, формируются следующим образом:
- Cоставляются все возможные последовательности из объектов из
- Перенумеруются всеми возможными способами.
Их принято обозначать .
-тый член выражается следующим образом:
Поэтому производящая функция —
Неограниченная конструкция
Определение не изменилось.
| Утверждение: |
| (Геометрическая прогрессия) |
Действует ограничение на , как и на и в формализме непомеченных объектов.
Пример
Перестановки
- Экспоненциальной производящей функцией является .
- Обычной производящей функции соответствует считающая последовательность , поэтому .
Урны
Кобинаторный класс "Урна" — множество, характеризующееся только количеством атомов в объекте, то есть элементов каждого веса — , поэтому .
Производящая функция этого класса — .
Множества
В формализме помеченных объектов , потому что не бывает одинаковых элементов в множествах.
Ограниченная конструкция
| Определение: |
| Ограниченным множеством назовём множество из объектов (порядок не важен). |
Рассмотрим и разобьем последовательности в на классы эквивалентности по признаку равенства множеств элементов в них.
Каждому биективно соответствует последовательностей в , потому что все объекты различны.
Неограниченная конструкция
— множества объектов (порядок не важен).
Ограничение также действует.
Можно рассматривать как композицию урны и , другими словами, можно вместо атомов в урне взять объекты класса .
Циклы
Ограниченная конструкция
| Определение: |
| Цикл — ориентированная циклическая последовательность из объектов класса . Циклов нулевой длины , то есть, . |
| Утверждение: |
Каждому циклу длины биективно соответствует упорядоченных последовательностей (циклические перестановки элементов цикла). |
Поэтому
Значит, экспоненциальная производящая функция циклов — .
Неограниченная конструкция
| Определение: |
| Циклы . |
(Разложение натурального логарифма в ряд Тейлора)
См.также
- Конструирование комбинаторных объектов и их подсчёт
- Функция Эйлера
- Лемма Бёрнсайда и Теорема Пойа
- Задача об ожерельях
- Числа Каталана
- Генерация комбинаторных объектов в лексикографическом порядке
- Подсчет деревьев