Суффиксный бор

Суффиксный бор для строки [math]abbc[/math]

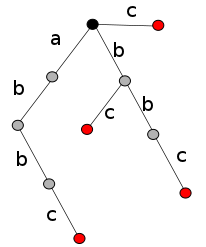
Суффиксный бор (suffix trie) - бор, содержащий все суффиксы данной строки.

По определению, в суффиксном боре для строки s содержатся все строки [math]s[1..n], ..., s[n..n][/math]. Сделаем следующее наблюдение: если в суффиксном боре находится строка [math]s[i..n][/math], то все символы строк вида [math]s[i..j], i \le j \le n[/math] уже содержатся в нашем боре. Значит, суффиксный бор можно использовать для поиска всех подстрок строки [math]s[/math] (чтобы бор формально содержал все подстроки [math]s[/math], нужно пометить все его вершины терминальными, при этом корень будет соответствовать пустой строке [math]\varepsilon[/math]).

Свойства

Суффиксный бор для строки [math]s[/math]:

• Можно использовать для поиска образца [math]p[/math] в строке [math]s[/math] за время [math]O(|p|)[/math].
• Можно построить за время [math]O(|s|^2)[/math], последовательно добавив все суфиксы [math]s[/math].
• Имеет порядка [math]n^2[/math] вершин.

Хранение в памяти

Пусть [math]s \in \Sigma^*[/math]. Из третьего свойства следует, что для хранения суффиксного бора в худшем случае потребуется [math]O(n^2 |\Sigma|)[/math] памяти. Если не хранить массив переходов по символам для вершин, где такой переход единственный, то можно получить оценку [math]O(n^2 + n|\Sigma|)[/math]. Улучшением суффиксного бора, расходующим всего [math]O( n|\Sigma|)[/math] памяти, является сжатое суффиксное дерево.