Обсуждение участника:Mishenkoil — различия между версиями
(→Применение симметричной версии локальной леммы) |
(копипаста) |
||
| Строка 1: | Строка 1: | ||
| − | + | [[Глубокое обучение|Глубокая сеть]] состоит из нескольких слоев, где каждый слой организован таким образом, что каждый нейрон в одном слое получает свою копию всех выходных данных предыдущего слоя. Эта модель идеально подходит для определенных типов задач, например, обучение на ограниченном количестве более или менее неструктурированных параметров. Существует множество способов изменения параметров (весов) в такой модели, когда ей на вход поступают необработанные данные. | |
| − | + | == Инициализация сети == | |
| − | + | Принцип выбора начальных значений весов для слоев, составляющих модель очень важен: установка всех весов в 0 будет серьезным препятствием для обучения, так как ни один из весов изначально не будет активен. Присваивать весам значения из интервала <tex>[-1, 1]</tex> — тоже обычно не лучший вариант — на самом деле, иногда (в зависимости от задачи и сложности модели) от правильной инициализации модели может зависеть, достигнет она высочайшей производительности или вообще не будет сходиться. Даже если задача не предполагает такой крайности, удачно выбранный способ инициализации весов может значительно влиять на способность модели к обучению, так как он предустанавливает параметры модели с учетом функции потерь<ref>[https://habr.com/company/wunderfund/blog/315476/ Тонкая настройка нейронной сети, Habr]</ref>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </tex> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | + | Всегда можно выбрать случайно начальное приближение, но лучше выбирать определённым образом, ниже приведены самые распространённые из них: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | + | * Метод инициализации Завьера (Xavier) (иногда — метод Glorot’а)<ref>[http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf Understanding the difficulty of training deep feedforward neural networks]</ref>. Основная идея этого метода — упростить прохождение сигнала через слой во время как прямого, так и обратного распространения ошибки для линейной функции активации (этот метод также хорошо работает для сигмоидной функции, так как участок, где она ненасыщена, также имеет линейный характер). При вычислении весов этот метод опирается на вероятностное распределение (равномерное или нормальное) с дисперсией, равной <tex>\mathrm{Var}(W) = {2 \over{n_{in} + n_{out}}}</tex>, где <tex>n_{in}</tex> и <tex>n_{out}</tex> — количества нейронов в предыдущем и последующем слоях соответственно; |
| − | | | + | |
| − | | | + | * Метод инициализации Ге (He) — вариация метода Завьера, больше подходящая функции активации ReLU, компенсирующая тот факт, что эта функция возвращает нуль для половины области определения. А именно, в этом случае <tex>\mathrm{Var}(W) = {2 \over{n_{in}}}</tex><ref>[https://arxiv.org/pdf/1502.01852.pdf Delving Deep into Rectifiers]</ref>. |
| − | | | + | |
| − | + | == Граф вычислений == | |
| − | }} | + | Глубокие сети являются особенной формой графа вычиcлений. |
| + | [[Файл: tree-def.png|450px|thumb|Рис.1. Граф вычислений для функции <tex>f(a,b)=(a+b)*(b+1)</tex>]] | ||
| + | Граф вычислений — ориентированный граф, узлы которого соответствуют операциям или переменным. Переменные могут передавать свое значение в операции, а операции могут передавать свои результаты в другие операции. Таким образом, каждый узел в графе определяет функцию переменных. | ||
| + | |||
| + | Значения, которые вводятся в узлы и выходят из узлов, называются тензорами (т.е. многомерными массивами). На рисунке 1 представлен граф вычислений для функции <tex>f(a,b)=(a+b)*(b+1)</tex>. В нейронах сетях функций имеют больше аргументов и сложнее, но смысл операций остаётся прежним. | ||
| + | |||
| + | Процесс передачи значений от входных нейронов к выходным называется прямым распространением (от англ. Forward pass). После чего мы вычисляем ошибку обработанных сетью данных на выходном нейроне и, основываясь на её значении, делаем обратную передачу ошибки ([[Обратное распространение ошибки|Back propagation]]). Обратное распространение ошибки заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значения весов будут меняться в сторону уменьшения ошибки. | ||
| + | |||
| + | [[Файл: C_graph.png|400px|thumb|Рис.2. Граф вычислений для функции <tex>f(x,y,z)=(x+y)*z</tex>. Зелёные цифры — значения вычислений по ходу выполнения операций графа, красные — значения производной выходной функции по текущей переменной в точке <tex>(x_0=-2, y_0=5, z_0=-4)</tex>]] | ||
| + | |||
| + | |||
| + | Преимуществом такого представления функции является простота вычисления производных. Используя следующие правила вычисления частных производных: | ||
| + | *<tex>q=x+y:\frac{\partial q}{\partial x}=1, \frac{\partial q}{\partial y}=1;</tex>; | ||
| + | *<tex>q=xy:\frac{\partial q}{\partial x}=y, \frac{\partial q}{\partial y}=x;</tex>; | ||
| + | *<tex>\frac{\partial f}{\partial y}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial y}</tex>. | ||
| + | |||
| + | Рассмотрим граф вычислений на рисунке 2 с поданными на вход значениями <tex>(x_0=-2, y_0=5, z_0=-4)</tex>. Подсчёт производных по графу вычислений производим от значения функции к значениям независимых переменных-входов. | ||
| + | |||
| + | * <tex>\frac{\partial f}{\partial f} = 1</tex>; | ||
| + | * <tex>\frac{\partial f}{\partial q} = z_0 = -4</tex>, <tex>\frac{\partial f}{\partial z} = q_0 = 3</tex>; | ||
| + | * <tex>\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial x} = -4</tex>, <tex>\frac{\partial f}{\partial y} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial y} = -4</tex>. | ||
| + | |||
| + | |||
| + | Граф вычислений является частью нейронной сети, у которой <tex>x_{n_{in}}</tex> {{---}} входные значения, <tex>y_{n_{out}}</tex> {{---}} выходные с сети значения, <tex>w</tex> {{---}} матрица весов, приводящая значения предыдущего слоя к выходным значениям. | ||
| + | |||
| + | Зная производные, можно искать матрицы весов <tex>w</tex> (числа, на которые умножаются входные для этого слоя значения) с помощью [[Настройка глубокой сети#Способы настройки параметров|градиентного спуска]] сдвигаемся | ||
| + | в сторону градиента (при максимизации) или обратную ему | ||
| + | (при минимизации) <tex>w^{(k+1)}=w^{(k)}-\eta \frac{\partial L(w^{(k)})}{\partial w^{(k)}}</tex>, где <tex>L</tex> — функция потерь, а <tex>w^{(k)}</tex> — веса после <tex>k</tex>-ой итерации, или его модификаций<ref>[http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D1%80%D0%B0%D0%B4%D0%B8%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D0%B3%D0%BE_%D1%81%D0%BF%D1%83%D1%81%D0%BA%D0%B0 Метод градиентного спуска]</ref>. | ||
| + | |||
| + | == Способы настройки параметров == | ||
| + | [[File:basins.png|450px|thumb|right|Рис.3. Сравение мотификаций метода градиентного спуска на ландшафте "бассейны и стены"<ref>[https://habr.com/post/318970/ Методы оптимизации нейронных сетей, Habr]</ref>.]] | ||
| + | [[File:wolby.png|450px|thumb|right|Рис.4. Сравение мотификаций метода градиентного спуска на "шатком" ландшафте<ref>[https://habr.com/post/318970/ Методы оптимизации нейронных сетей, Habr]</ref>.]] | ||
| + | Ниже представлены различные вариации градиентного спуска (более подробное сравнение, применительно к данной задаче <ref>[https://habr.com/post/318970/ Методы оптимизации нейронных сетей, Habr]</ref>). Градиентный спуск — итеративный алгоритм поиска минимума или максимума функции, метриками качества алгоритма этого семейства методов являются скорость сходимости и сходимость в глобальный оптимум. Методы имеют различные преимущества на различных функциях. Так например на рисунке 3 из локального минимума метод adam и метод Нестерова не могут достигнуть глобального, а в случае "шаткого" ландшафта (рисунок 4) эти методы сходятся быстрее. | ||
| + | |||
| + | * [[Стохастический градиентный спуск|Метод стохастического градиентного спуска]] заключается в том, что алгоритм делает шаг постоянной величины в направлении, указанном градиентом в текущей точке: <tex>w^{(k+1)}=w^{(k)}-\mu\frac{\partial L(w^{(k)})}{\partial w^{(k)}}</tex>; | ||
| + | |||
| + | |||
| + | * Модификация Momentum <ref>[https://en.wikipedia.org/wiki/Stochastic_gradient_descent#Momentum Momentum, Wikipedia]</ref> запоминает скорость на предыдущем шаге и добавляет в <tex>\alpha</tex> раз меньшую величину на следующем шаге: <tex> v^{(k+1)}=\alpha v^{(k)} -\eta \frac{\partial L(w^{(k)})}{\partial w^{(k)}}</tex>, <tex> w^{(k+1)}=w^{(k)}+v^{(k)}</tex>; | ||
| + | |||
| + | |||
| + | * Метод Нестерова (англ. Nesterov accelerated gradient, NAG)<ref>[https://jlmelville.github.io/mize/nesterov.html#nag Nesterov accelerated gradient]</ref> добавляет к методу Momentum идею "заглядывания вперёд", используя производную не в текущей точке, а в следующей (если бы мы продолжали двигаться в этом же направлении без измений): <tex> w^{(k+1)} = w^{(k)}-v^{(k)}; v^{(k+1)}=\gamma v^{(k)}+\mu\frac{\partial L(w^{(k)}-v^{(k)})}{\partial w}</tex>; | ||
| + | |||
| + | |||
| + | *Adagrad имеет преимущество в плане обучения нейронных сетей в предположении, что процесс обучения должен сходится (т.е. не нужно сильно менять веса сети, когда мы уже немного научились). В процессе обучения после каждого прецендента алгоритм будет уменьшать шаг за счёт суммы квадратов координат градиента предыдущих итераций<ref>[http://akyrillidis.github.io/notes/AdaGrad AdaGrad]</ref>: <tex>g_i^{(k)}=\frac{\partial L(w_i^{(k)})}{\partial w_i^{(k)}}, w_i^{(k+1)}=w_i^{(k)}-\frac{\mu}{\sqrt{G^{(k)}_{i,i}+\epsilon}}g_{i}^{(k)}</tex>, где <tex>G</tex> — диагональная матрица, элементы которой, суммы квадратов координат градиента к <tex>k</tex>-ой итерации алгоритма: <tex>G_{i,i}^{(k)} = \sum_{t=0}^k (g_i^{(t)})^2</tex>; | ||
| + | |||
| + | |||
| + | *RMSProp<ref>[https://towardsdatascience.com/a-look-at-gradient-descent-and-rmsprop-optimizers-f77d483ef08b RMSProp]</ref> основан на идее Adagrad'a, но с учётом того элементы матрицы <tex>G</tex> могут быть большими величинами и начать препятствовать обучению. Для этого RMSProp делит шаг не на полную сумму градиентов, а на скользящую, т.е. <tex>E_i^{(k)} = \gamma E_i^{(k-1)}+(1-\gamma)(g_{i}^{(k)})^2</tex>, обновление весов осталось таким же как в Adagrad : <tex> w_i^{(k+1)} = w_i^{(k)}-\frac{\mu}{\sqrt{E_i^{(k)}+\epsilon}}g_{i}^{(k)}</tex>; | ||
| + | |||
| + | |||
| + | *Adadelta<ref>[https://arxiv.org/abs/1212.5701 Adadelta]</ref> устраняет "нефизичность" методов Adagrad и RMSProp, добавка с градиентом в которых не имеет размерности весов(точнее вообще безразмерна). Умножение этого слагаемого на любую величину правильной размерности — не самая хорошая идея. Используем разложение ряда Тейлора в точке с большим числом членов, тогда появится матрица <tex>Q</tex> вторых производных функции потерь: <tex>w^{(k+1)}=w^{(k)}-\mu(Q(w^{(k)})^{-1}Q(w^{(k)}))</tex>, рассчёт которой повлечёт за собой дополнительные затраты на её расчёт (сами градиенты мы получаем сразу при обратном распространии ошибки), поэтому вместо неё можно брать приближение (из сложных выводов получаем необходимиый множитель <tex>RMS^{(k-1)}[\delta w_i]</tex>), однако в данном случае знание предыдущей скорости не добавляет алгоритму "инерции" методов Momentum и NAG): <tex>w^{(k+1)}=w^{(k)}-\frac{RMS^{(k-1)}[\delta w_i]}{RMS^{(k)}[g_i]}g_i^{(k)}</tex>, где <tex>RMS^{(k)}[x_i]=\sqrt{E^{(k)}[x^2_i]+\epsilon}</tex>; | ||
| + | |||
| + | |||
| + | *Adam<ref>[https://arxiv.org/pdf/1412.6980.pdf Adam]</ref> сочетает в себе преимущества NAG и Adadelta над обычным градиентным спуском: <tex> w^{(k+1)}_i = w_i^{(k)}-\frac{\mu}{\sqrt{\hat{b}^2_{(k)}+\epsilon}}\hat{m}_{(k)}</tex>, где <tex>\hat{m}_{(k)}=\frac{\gamma_1 E^{(k-1)}[g_i]+(1-\gamma_1)g_{i,(k)}}{1-\gamma_1^k}</tex> и <tex>\hat{b}^2_{(k)}= \frac{\gamma_2 E^{(k-1)}[g^2_i]+(1-\gamma_2)g:2_{i,(k)}}{1-\gamma_2^k}</tex>. | ||
| + | |||
| + | == Сравнение способов настройки параметров == | ||
| + | [[Файл:Gradient_optimization.gif|Сравнение разных методов на седловой функции]] | ||
| + | |||
| + | Рассмотрим график седловой функции с "седлом" в точке <tex>(0, 0, 0)</tex>. Предположим, что в качестве начальной точки выбрана точка <tex>(0, y, z)</tex>, где <tex>y > 0, z > 0</tex>. На рисунке координата <tex>x</tex> варьируется в пределах от <tex>-1.5</tex> до <tex>1</tex>, координата <tex>y \in [-0.5; 1]</tex>, а координата <tex>z \in [-4; 4]</tex>. Рассмотрим работу описанных выше методов, примененных к данной оптимизируемой функции с данной начальной точкой: | ||
| + | |||
| + | * SGD (Стандартный градиентный спуск без оптимизаций) никак не учитывает тот факт, что по координате <tex>x</tex> производная в данной точке пренебрежимо мала по сравнению с производной по <tex>y</tex>. Поэтому через малое число итераций алгоритм сойдется в окрестности седловой точки <tex>(0, 0, 0)</tex> и остановится, потому что производная в данной точке нулевая. | ||
| + | |||
| + | * Momentum. Так как добавится инерция, то спуск в сторону седловой точки будет значительно быстрее, чем в случае со стандартным градиентным спуском. Однако, оптимизируемая переменная будет еще долго колебаться в плоскости <tex>x = 0</tex>, накапливая градиенты. При этом колебания будут затухать из-за того, что параметр <tex>\alpha < 1</tex>, но т.к. оптимизируемая переменная несколько раз отдалится от точки <tex>(0, 0, 0)</tex> на достаточное расстояние, успеет накопиться значение производной по координате <tex>x</tex>, достаточное для того чтобы выйти из локального минимума. Однако для этого потребуется большое число итераций, необходимое для того, чтобы производная по <tex>y</tex> перестала преобладать над производной по <tex>x</tex>. | ||
| + | |||
| + | * NAG. Эффект будет схожим с алгоритмом Momentum, однако спуск в плоскости <tex>y = 0</tex> будет происходить быстрее благодаря заглядыванию вперед. | ||
| + | |||
| + | * Adagrad. Изначально спуск будет происходить медленнее, чем при использовании SGD из-за нормирования градиента по всем координатам, однако метод сойдется в глобальном минимуме выбранной области графика. | ||
| + | |||
| + | * RMSProp. Изначально процесс оптимизации почти совпадает с Adagrad, но в области, где функция начинает сильно убывать, благодаря использованию скользящей суммы градиентов (то есть благодаря тому, что мы забываем старые изменения и больше учитываем новые) алгоритм RMSProp оптимизирует переменную быстрее, чем Adagrad. | ||
| + | |||
| + | * Adadelta. Использует все преимущества RMSProp, но при этом в данном случае сходится быстрее в <tex>RMS[\delta w_i]</tex> раз. | ||
| + | |||
| + | ==См.также== | ||
| + | * [[Глубокое обучение]] | ||
| + | * [[Стохастический градиентный спуск]] | ||
| + | * [[Обратное распространение ошибки]] | ||
| + | |||
| + | ==Примечания== | ||
| + | <references/> | ||
| + | |||
| + | ==Источники информации== | ||
| + | |||
| + | #[http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BE%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29 Курс лекций по машинному обучению] {{---}} Воронцов К.В. | ||
| + | # Riedmiller, M., & Braun, H. (1993). A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Neural Networks, 1993., IEEE International Conference on (pp. 586-591). IEEE. | ||
| + | |||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Глубокое обучение]] | ||
==Применение симметричной версии локальной леммы== | ==Применение симметричной версии локальной леммы== | ||
Версия 22:39, 8 мая 2022
Глубокая сеть состоит из нескольких слоев, где каждый слой организован таким образом, что каждый нейрон в одном слое получает свою копию всех выходных данных предыдущего слоя. Эта модель идеально подходит для определенных типов задач, например, обучение на ограниченном количестве более или менее неструктурированных параметров. Существует множество способов изменения параметров (весов) в такой модели, когда ей на вход поступают необработанные данные.
Содержание
Инициализация сети
Принцип выбора начальных значений весов для слоев, составляющих модель очень важен: установка всех весов в 0 будет серьезным препятствием для обучения, так как ни один из весов изначально не будет активен. Присваивать весам значения из интервала — тоже обычно не лучший вариант — на самом деле, иногда (в зависимости от задачи и сложности модели) от правильной инициализации модели может зависеть, достигнет она высочайшей производительности или вообще не будет сходиться. Даже если задача не предполагает такой крайности, удачно выбранный способ инициализации весов может значительно влиять на способность модели к обучению, так как он предустанавливает параметры модели с учетом функции потерь[1].
Всегда можно выбрать случайно начальное приближение, но лучше выбирать определённым образом, ниже приведены самые распространённые из них:
- Метод инициализации Завьера (Xavier) (иногда — метод Glorot’а)[2]. Основная идея этого метода — упростить прохождение сигнала через слой во время как прямого, так и обратного распространения ошибки для линейной функции активации (этот метод также хорошо работает для сигмоидной функции, так как участок, где она ненасыщена, также имеет линейный характер). При вычислении весов этот метод опирается на вероятностное распределение (равномерное или нормальное) с дисперсией, равной , где и — количества нейронов в предыдущем и последующем слоях соответственно;
- Метод инициализации Ге (He) — вариация метода Завьера, больше подходящая функции активации ReLU, компенсирующая тот факт, что эта функция возвращает нуль для половины области определения. А именно, в этом случае [3].
Граф вычислений
Глубокие сети являются особенной формой графа вычиcлений.
Граф вычислений — ориентированный граф, узлы которого соответствуют операциям или переменным. Переменные могут передавать свое значение в операции, а операции могут передавать свои результаты в другие операции. Таким образом, каждый узел в графе определяет функцию переменных.
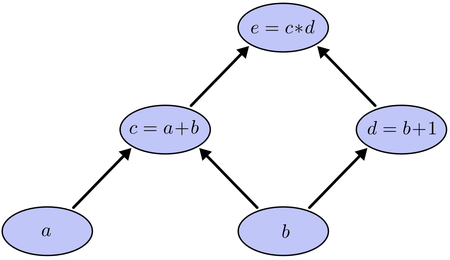
Значения, которые вводятся в узлы и выходят из узлов, называются тензорами (т.е. многомерными массивами). На рисунке 1 представлен граф вычислений для функции . В нейронах сетях функций имеют больше аргументов и сложнее, но смысл операций остаётся прежним.
Процесс передачи значений от входных нейронов к выходным называется прямым распространением (от англ. Forward pass). После чего мы вычисляем ошибку обработанных сетью данных на выходном нейроне и, основываясь на её значении, делаем обратную передачу ошибки (Back propagation). Обратное распространение ошибки заключается в том, чтобы последовательно менять веса нейронной сети, начиная с весов выходного нейрона. Значения весов будут меняться в сторону уменьшения ошибки.
Преимуществом такого представления функции является простота вычисления производных. Используя следующие правила вычисления частных производных:
- ;
- ;
- .
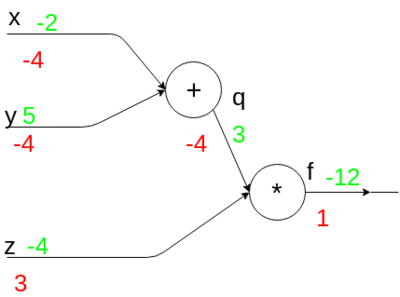
Рассмотрим граф вычислений на рисунке 2 с поданными на вход значениями . Подсчёт производных по графу вычислений производим от значения функции к значениям независимых переменных-входов.
- ;
- , ;
- , .
Граф вычислений является частью нейронной сети, у которой — входные значения, — выходные с сети значения, — матрица весов, приводящая значения предыдущего слоя к выходным значениям.
Зная производные, можно искать матрицы весов (числа, на которые умножаются входные для этого слоя значения) с помощью градиентного спуска сдвигаемся в сторону градиента (при максимизации) или обратную ему (при минимизации) , где — функция потерь, а — веса после -ой итерации, или его модификаций[4].
Способы настройки параметров
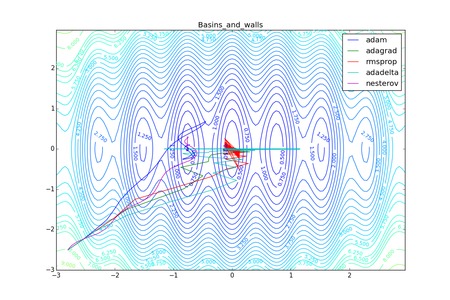
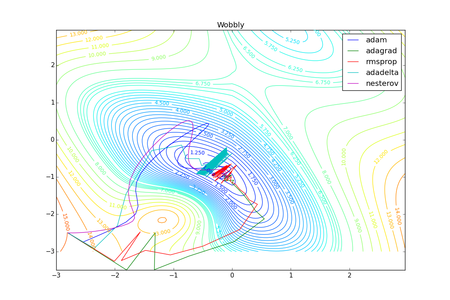
Ниже представлены различные вариации градиентного спуска (более подробное сравнение, применительно к данной задаче [7]). Градиентный спуск — итеративный алгоритм поиска минимума или максимума функции, метриками качества алгоритма этого семейства методов являются скорость сходимости и сходимость в глобальный оптимум. Методы имеют различные преимущества на различных функциях. Так например на рисунке 3 из локального минимума метод adam и метод Нестерова не могут достигнуть глобального, а в случае "шаткого" ландшафта (рисунок 4) эти методы сходятся быстрее.
- Метод стохастического градиентного спуска заключается в том, что алгоритм делает шаг постоянной величины в направлении, указанном градиентом в текущей точке: ;
- Модификация Momentum [8] запоминает скорость на предыдущем шаге и добавляет в раз меньшую величину на следующем шаге: , ;
- Метод Нестерова (англ. Nesterov accelerated gradient, NAG)[9] добавляет к методу Momentum идею "заглядывания вперёд", используя производную не в текущей точке, а в следующей (если бы мы продолжали двигаться в этом же направлении без измений): ;
- Adagrad имеет преимущество в плане обучения нейронных сетей в предположении, что процесс обучения должен сходится (т.е. не нужно сильно менять веса сети, когда мы уже немного научились). В процессе обучения после каждого прецендента алгоритм будет уменьшать шаг за счёт суммы квадратов координат градиента предыдущих итераций[10]: , где — диагональная матрица, элементы которой, суммы квадратов координат градиента к -ой итерации алгоритма: ;
- RMSProp[11] основан на идее Adagrad'a, но с учётом того элементы матрицы могут быть большими величинами и начать препятствовать обучению. Для этого RMSProp делит шаг не на полную сумму градиентов, а на скользящую, т.е. , обновление весов осталось таким же как в Adagrad : ;
- Adadelta[12] устраняет "нефизичность" методов Adagrad и RMSProp, добавка с градиентом в которых не имеет размерности весов(точнее вообще безразмерна). Умножение этого слагаемого на любую величину правильной размерности — не самая хорошая идея. Используем разложение ряда Тейлора в точке с большим числом членов, тогда появится матрица вторых производных функции потерь: , рассчёт которой повлечёт за собой дополнительные затраты на её расчёт (сами градиенты мы получаем сразу при обратном распространии ошибки), поэтому вместо неё можно брать приближение (из сложных выводов получаем необходимиый множитель ), однако в данном случае знание предыдущей скорости не добавляет алгоритму "инерции" методов Momentum и NAG): , где ;
- Adam[13] сочетает в себе преимущества NAG и Adadelta над обычным градиентным спуском: , где и .
Сравнение способов настройки параметров
Рассмотрим график седловой функции с "седлом" в точке . Предположим, что в качестве начальной точки выбрана точка , где . На рисунке координата варьируется в пределах от до , координата , а координата . Рассмотрим работу описанных выше методов, примененных к данной оптимизируемой функции с данной начальной точкой:
- SGD (Стандартный градиентный спуск без оптимизаций) никак не учитывает тот факт, что по координате производная в данной точке пренебрежимо мала по сравнению с производной по . Поэтому через малое число итераций алгоритм сойдется в окрестности седловой точки и остановится, потому что производная в данной точке нулевая.
- Momentum. Так как добавится инерция, то спуск в сторону седловой точки будет значительно быстрее, чем в случае со стандартным градиентным спуском. Однако, оптимизируемая переменная будет еще долго колебаться в плоскости , накапливая градиенты. При этом колебания будут затухать из-за того, что параметр , но т.к. оптимизируемая переменная несколько раз отдалится от точки на достаточное расстояние, успеет накопиться значение производной по координате , достаточное для того чтобы выйти из локального минимума. Однако для этого потребуется большое число итераций, необходимое для того, чтобы производная по перестала преобладать над производной по .
- NAG. Эффект будет схожим с алгоритмом Momentum, однако спуск в плоскости будет происходить быстрее благодаря заглядыванию вперед.
- Adagrad. Изначально спуск будет происходить медленнее, чем при использовании SGD из-за нормирования градиента по всем координатам, однако метод сойдется в глобальном минимуме выбранной области графика.
- RMSProp. Изначально процесс оптимизации почти совпадает с Adagrad, но в области, где функция начинает сильно убывать, благодаря использованию скользящей суммы градиентов (то есть благодаря тому, что мы забываем старые изменения и больше учитываем новые) алгоритм RMSProp оптимизирует переменную быстрее, чем Adagrad.
- Adadelta. Использует все преимущества RMSProp, но при этом в данном случае сходится быстрее в раз.
См.также
Примечания
- ↑ Тонкая настройка нейронной сети, Habr
- ↑ Understanding the difficulty of training deep feedforward neural networks
- ↑ Delving Deep into Rectifiers
- ↑ Метод градиентного спуска
- ↑ Методы оптимизации нейронных сетей, Habr
- ↑ Методы оптимизации нейронных сетей, Habr
- ↑ Методы оптимизации нейронных сетей, Habr
- ↑ Momentum, Wikipedia
- ↑ Nesterov accelerated gradient
- ↑ AdaGrad
- ↑ RMSProp
- ↑ Adadelta
- ↑ Adam
Источники информации
- Курс лекций по машинному обучению — Воронцов К.В.
- Riedmiller, M., & Braun, H. (1993). A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Neural Networks, 1993., IEEE International Conference on (pp. 586-591). IEEE.
Применение симметричной версии локальной леммы
| Задача: |
| Пусть $G$ - граф, степени всех вершин которого не больше $d$, $P_i$ - непересекающиеся подмножества множества вершин графа $G$ такие, что . Тогда можно выбрать в каждом $P_i$ по вершине так, что никакие две соединенные ребром вершины не будут выбраны. |
Решение:
Уменьшим при необходимости некоторые $P_i$ так, чтобы для всех $i$ выполнялось , где . Будем выбирать вершины случайно и независимо. Каждому ребру графа $G$ сопоставим событие $A_{(u, v)}$, обозначающее, что оба конца $u$, $v$ этого ребра выбраны. Вероятность каждого такого события не больше, чем $1/k^2$. В случае, если концы ребра принадлежат одному и тому же $P_i$ или один из них не принадлежит ни одному $P_i$, вероятность такого события равна
$0$ и такие $A_{(u, v)}$ мы далее не рассматриваем. Для ребра $(u, v)$, для которого, скажем , рассмотрим все ребра, выходящие из вершин множеств $P_1$ и $P_2$. Таких ребер, не считая ребра $(u, v)$, будет не более,
чем $2kd - 2$. Заметим, что событие $A_{(u, v)}$ не зависит от всех других событий типа , где - ребро, соединяющее вершины множеств, отличных от $P_1$ и $P_2$.
Таким образом, для применения симметричной версии локальной леммы достаточно проверить, что , что имеет место.