Splay-дерево — различия между версиями
Forgotenn (обсуждение | вклад) |
Forgotenn (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
Пусть <tex> p(x) </tex> - предок вершины <tex> x </tex>. | Пусть <tex> p(x) </tex> - предок вершины <tex> x </tex>. | ||
Эвристика "Move to Root" совершает повороты вокруг ребра <tex> \langle x, p(x) \rangle </tex>, пока <tex> x </tex> не окажется корнем дерева. | Эвристика "Move to Root" совершает повороты вокруг ребра <tex> \langle x, p(x) \rangle </tex>, пока <tex> x </tex> не окажется корнем дерева. | ||
| − | + | Данный поворот аналогичен zig - повороту. | |
==Splay== | ==Splay== | ||
"Splay" так же как и "Move to Root" перетаскивает вершину в корень дерева, но при этом она использует другую последовательность поворотов. Пока <tex> x </tex> не является корнем дерева выполняется следующее : | "Splay" так же как и "Move to Root" перетаскивает вершину в корень дерева, но при этом она использует другую последовательность поворотов. Пока <tex> x </tex> не является корнем дерева выполняется следующее : | ||
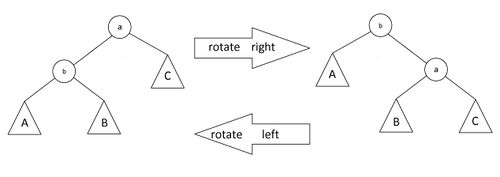
# Zig. Если <tex> p(x) </tex> - корень дерева, то совершаем один поворот вокруг ребра <tex> \langle x, p(x) \rangle </tex>, делая <tex> x </tex> корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина <tex> x </tex> была нечетной. | # Zig. Если <tex> p(x) </tex> - корень дерева, то совершаем один поворот вокруг ребра <tex> \langle x, p(x) \rangle </tex>, делая <tex> x </tex> корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина <tex> x </tex> была нечетной. | ||
| + | [[file:zig.jpg|500px|Zig - поворот]] | ||
# Zig-Zig. Если <tex> p(x) </tex> - не корень дерева, а <tex> x </tex> и <tex> p(x) </tex> - оба левые или оба правые дети, то делаем поворот ребра <tex> \langle p(x), p(p(x)) \rangle </tex>, а затем поворот ребра <tex> \langle x, p(x) \rangle </tex>. | # Zig-Zig. Если <tex> p(x) </tex> - не корень дерева, а <tex> x </tex> и <tex> p(x) </tex> - оба левые или оба правые дети, то делаем поворот ребра <tex> \langle p(x), p(p(x)) \rangle </tex>, а затем поворот ребра <tex> \langle x, p(x) \rangle </tex>. | ||
# Zig-Zag. Если <tex> p(x) </tex> - не корень дерева и <tex> x </tex> - левый ребенок, а <tex> p(x) </tex> - правый, или наоборот, то делаем поворот вокруг ребра <tex> \langle x, p(x) \rangle </tex>, а затем поворот нового ребра <tex> \langle x, p(x) \rangle </tex>, где <tex> p(x) </tex> - новый родитель <tex> x </tex>. | # Zig-Zag. Если <tex> p(x) </tex> - не корень дерева и <tex> x </tex> - левый ребенок, а <tex> p(x) </tex> - правый, или наоборот, то делаем поворот вокруг ребра <tex> \langle x, p(x) \rangle </tex>, а затем поворот нового ребра <tex> \langle x, p(x) \rangle </tex>, где <tex> p(x) </tex> - новый родитель <tex> x </tex>. | ||
Версия 23:52, 26 апреля 2011
Сплей-дерево (Splay-tree) — саморегулирующееся двоичное дерево поиска. Относится к разряду сливаемых деревьев. Сплей-дерево было придумано Робертом Тарьяном и Даниелем Слейтером в 1983 году.
Основной идей для сохранение баланса дерева является перетаскивание найденной вершины в корень после каждой операции поиска.
Move to Root
Пусть - предок вершины . Эвристика "Move to Root" совершает повороты вокруг ребра , пока не окажется корнем дерева. Данный поворот аналогичен zig - повороту.
Splay
"Splay" так же как и "Move to Root" перетаскивает вершину в корень дерева, но при этом она использует другую последовательность поворотов. Пока не является корнем дерева выполняется следующее :
- Zig. Если - корень дерева, то совершаем один поворот вокруг ребра , делая корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина была нечетной.
- Zig-Zig. Если - не корень дерева, а и - оба левые или оба правые дети, то делаем поворот ребра , а затем поворот ребра .
- Zig-Zag. Если - не корень дерева и - левый ребенок, а - правый, или наоборот, то делаем поворот вокруг ребра , а затем поворот нового ребра , где - новый родитель .
Данная операция занимает времени, где - длина пути от до корня. В результате этой операции становится корнем дерева, а расстояние до корня от каждой вершины сокращается примерно пополам, что связано с разделением случаев "zig-zig" и "zig-zag".
Литература
- Daniel Sleator, Robert Tarjan "A data structure for dynamic trees"