Обнаружение и исправление ошибок кодирования

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Пусть [math]B = \{0, 1\}[/math] — булевое множество. Рассмотрим [math]B^n[/math] и расстояние Хемминга [math]H(x,y)[/math]. Пусть [math]c:\Sigma \to B^n[/math] — разделяемый код постоянной длины. Обозначим [math]d(c) = \min\limits_{\substack{x, y\in \Sigma \\ x\neq y}}H(c(x), c(y))[/math].

Коды, обнаруживающие и исправляющие ошибки

Определение:

Код [math]c[/math] обнаруживает [math]k[/math] ошибок, если [math]d(c) \gt k[/math].

Определение:

Код [math]c[/math] исправляет [math]k[/math] ошибок, если [math]d(c) \gt 2k[/math].

Утверждение:

Код, исправляющий [math]k[/math] ошибок, обнаруживает [math]2k[/math] ошибок.

Булев шар

Определение:

Булев шар — подмножество [math]B^n[/math] вида [math] \{ y : H(x,y) \leqslant r\}[/math]. [math]x[/math] называется его центром, [math]r[/math] — радиусом. Булев шар с центром [math]x[/math] и радиусом [math]r[/math] обознчается [math]S(x,r)[/math].

Определение:

Обьёмом шара [math]S(x,r)[/math] в [math]B^n[/math] называется величина [math]|S(x,r)|[/math]. Обьём шара радиуса [math]r[/math] в [math]B^n[/math] обозначается [math]V(n,r)[/math].

Утверждение:

Обьём шара не зависит от его центра.

[math]\triangleright[/math]

Заметим, что шар [math]S(x,r)[/math] всегда можно получить из другого шара [math]S(y,r)[/math] с помощью "параллельного переноса" на вектор [math]x\oplus y[/math] (здесь [math]\oplus[/math] обозначает побитовый [math]XOR[/math]), т.е. [math] S(x, r) = \{z : z = t \oplus x \oplus y, t \in S(y,r) \} [/math]. Покажем это. Необходимо доказать, что [math]H(x,z) = H(y,t)[/math] при [math]t = z \oplus (x \oplus y)[/math] и [math]y = x \oplus (x \oplus y)[/math]. [math]H(y,t) = |\{i : y[i] \neq t[i]\}| = |\{i : x[i] \oplus (x[i] \oplus y[i]) \neq z[i] + (x[i] + y[i])\}| = |\{i : x[i] \neq z[i]\}| = H(z,t) [/math].

[math]\triangleleft[/math]

Можно сформулировать свойство кодов, исправляющих [math]k[/math] ошибок, в терминах булевых шаров.

Лемма:

Пусть [math]c:\Sigma \to B^n[/math] — код, исправляющий [math]k[/math] ошибок. Тогда для любых неравных [math]x,y\in \Sigma[/math] выполнено [math]S(c(x), k) \cap S(c(y), k) = \emptyset[/math].

Доказательство:

[math]\triangleright[/math]

Т.к код [math]c[/math] исправляет [math]k[/math] ошибок, по определению [math]d(c)\gt 2k[/math]. Допустим, [math]x, y[/math] такие, что [math]x \neq y[/math] и [math]S(c(x), k) \cap S(c(y), k)\neq \emptyset[/math], т.е существует [math]z[/math], такой что [math]H(c(x), z) \leqslant k[/math] и [math]H(c(y), z) \leqslant k[/math]. Тогда по неравенству треугольника [math]H(c(x), c(y)) \leqslant 2k[/math]. Это противоречит тому, что [math]d(c)\gt 2k[/math].

[math]\triangleleft[/math]

Определение и устранение ошибок в общем случае

Пусть [math]\Sigma[/math] — исходный алфавит, [math]c: \Sigma \to B^m[/math] — кодирование, [math]B=(0,1)[/math]

[math]d: B^m \times B^m \to \mathbb{R}[/math] — расстояние Хэмминга между двумя кодами.

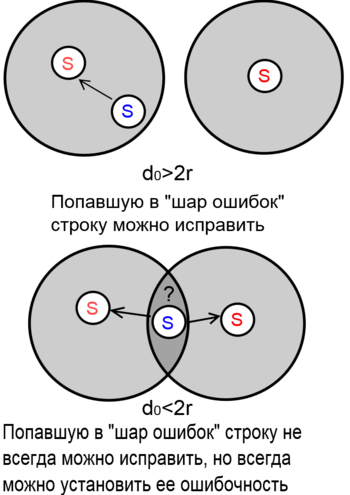
Код, [math]c: \Sigma \to B^m[/math] может исправлять [math]~[[/math][math] {d_0-1}\over{2}[/math][math]~][/math] и обнаруживать [math][d_0-1][/math] ошибок. Действительно, при любом натуральном количестве допустимых ошибок [math]r[/math] любоое кодовое слово [math]S[/math] образует вокруг себя проколотый шар таких строк [math]S_i[/math], что [math]0\lt d(S,S_i)\leqslant r[/math]. Если этот шар не содержит других кодов (что выполняется при [math]r\lt d_0[/math]) , то можно утверждать, что если в него попадает строка, то она ошибочна. Если шары всех кодов не пересекаются (что выполняется при [math]r \leqslant {{d_0-1}\over{2}} [/math]), то попавшую в шар строку [math]S_i[/math] можно считать ошибочной и исправить на центр шара — строку [math]S[/math].

Граница Хэмминга, граница Гильберта

Теорема (Граница Хэмминга):

Пусть [math]c: \Sigma \to B^n[/math] — код для [math]m[/math]-символьного алфавита, исправляющий [math]k[/math] ошибок. Тогда выполнено неравенство [math]mV(n,k) \leqslant 2^n[/math].

Доказательство:

[math]\triangleright[/math]

Это прямое следствие предыдущей леммы. Всего есть [math]m = |\Sigma|[/math] попарно непересекающихся шаров. Их суммарный обьём равен [math]mV(n,k)[/math], и он не может превосходить общее число возможных веткоров [math]|B| = 2^n[/math].

[math]\triangleleft[/math]

Граница Хэмминга даёт верхнюю оценку на скорость передачи сообщений в канале с ошибками. Прологарифмировав неравенство, получим [math]\frac{\log(m)}{n} \leqslant 1 - \frac{V(n, k)}{n}[/math]. Здесь [math]\frac{\log(m)}{n}[/math] это плотность кодирования, количество информации в одном символе алфавита на размер кода. Таким образом, при кодировании с защитой от ошибок падает скорость передачи.

Аналогично составляется оценка в другую сторону.

Теорема (Граница Гильберта):

Если выполнено неравенство [math] mV(n,2k) \leqslant 2^n[/math], то существует код [math]c:\Sigma \to B^n[/math] для [math]m[/math]-символьного алфавита [math]\Sigma [/math], исправляющий [math]k[/math] ошибок.

Примером кода для случая [math]k=1[/math] является код Хэмминга.

См. также

• Избыточное кодирование, код Хэмминга