Дерево, эквивалентные определения

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Определение:

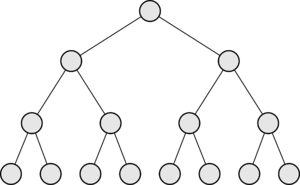
Дерево (англ. tree) — связный ациклический граф.

Определение:

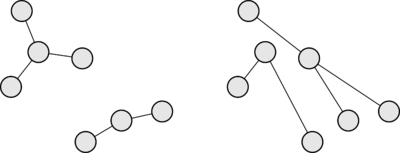
Лес (англ. forest) — граф, являющийся набором непересекающихся деревьев.

Определения

Для графа [math]G[/math] эквивалентны следующие утверждения:

1. [math]G[/math] — дерево.
2. Любые две вершины графа [math]G[/math] соединены единственным простым путем.
3. [math]G[/math] — связен и [math] p = q + 1 [/math], где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер.
4. [math]G[/math] — ацикличен и [math] p = q + 1 [/math], где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер.
5. [math]G[/math] — ацикличен и при добавлении любого ребра для несмежных вершин появляется один простой цикл.
6. [math]G[/math] — связный граф, отличный от [math] K_p [/math] для [math] p \gt 3 [/math], а также при добавлении любого ребра для несмежных вершин появляется один простой цикл.
7. [math]G[/math] — граф, отличный от [math] K_3 \cup K_1 [/math] и [math] K_3 \cup K_2 [/math], а также [math] p = q + 1 [/math], где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер, и при добавлении любого ребра для несмежных вершин появляется один простой цикл.

Доказательство эквивалентности

[math] 1 \Rightarrow 2 [/math]

Граф связен, поэтому любые две вершнины соединены путем. Граф ацикличен, значит путь единственен, а также прост, поскольку никакой путь не может зайти в одну вершину два раза, потому что это противоречит ацикличности.

[math] 2 \Rightarrow 3 [/math]

Очевидно, что граф связен. Докажем по индукции, соотношение [math]p = q + 1[/math]. Утверждение очевидно для связных графов с одной и двумя вершинами. Предположим, что оно верно для графов, имеющих меньше [math]p[/math] вершин. Если же граф [math]G[/math] имеет [math]p[/math] вершин, то удаление из него любого ребра делает граф [math] G [/math] несвязным в силу единственности простых цепей; более того, получаемый граф будет иметь в точности две компоненты. По предположению индукции в каждой компоненте число вершин на единицу больше числа ребер. Таким образом, [math] p = q + 1 [/math].

[math] 3 \Rightarrow 4 [/math]

Очевидно, что если граф связен и ребер на одно меньше, чем вершин, то он ацикличен. Преположим, что у нас есть p вершин, и мы добавляем ребра. Если мы добавили ребро для получения цикла, то добавили второй путь между парой вершин, а значит нам не хватит его на добавление вершины и мы получим не связный граф, что противоречит условию.

[math] 4 \Rightarrow 5 [/math]

[math]G[/math] — ациклический граф, значит каждая компонента связности графа является деревом. Так как в каждой из них вершин на единицу больше чем ребер, то [math] p = q + k [/math], где [math]k[/math] — число компонент связности. Поскольку [math] p = q + k [/math], то [math] k = 1 [/math], а значит [math]G[/math] — связен. Таким образом наш граф — дерево, у которого между любой парой вершин есть единственный простой путь. Очевидно, при добавлении ребра появится второй путь между парой вершин, то есть мы получим цикл.

[math] 5 \Rightarrow 6 [/math]

Поскольку [math] K_p [/math] для [math] p \gt 3 [/math] содержит простой цикл, то [math]G[/math] не может им являться. [math]G[/math] связен, так как в ином случае можно было бы добавить ребро так, что граф остался бы ациклическим.

[math] 6 \Rightarrow 7 [/math]

Докажем, что любые две вершины графа соединены единственной простой цепью, а тогда поскольку [math] 2 \Rightarrow 3 [/math], получим [math] p = q + 1 [/math]. Любые две вершины соединены простой цепью, так как [math]G[/math] — связен. Если две вершины соединены более чем одной простой цепью, то мы получим цикл. Причем он должен являться [math] K_3 [/math], так как иначе добавив ребро, соединяющее две вершины цикла, мы получим более одного простого цикла, что противоречит условию. [math] K_3 [/math] является собственным подграфом [math]G[/math], поскольку [math]G[/math] не является [math] K_p [/math] для [math] p \gt 3 [/math]. [math]G[/math] — связен, а значит есть вершина смежная с [math] K_3 [/math]. Очевидно, можно добавить ребро так, что образуется более одного простого цикла. Если нельзя добавить ребра так, чтобы не нарушалось исходное условие, то граф [math]G[/math] является [math]K_p[/math] для [math] p \gt 3 [/math], и мы получаем противоречие с исходным условием. Значит, любые две вершины графа соединены единственной простой цепью, что и требовалось.

[math] 7 \Rightarrow 1 [/math]

Если [math]G[/math] имеет простой цикл, то он является отдельной компонентой [math]K_3[/math] по ранее доказанному. Все остальные компоненты должны быть деревьями, но для выполнения соотношения [math] p = q + 1 [/math] должно быть не более одной компоненты отличной от [math]K_3[/math], так как в [math]K_3[/math] [math] p = q = 3 [/math]. Если это дерево содержит простой путь длины 2, то в [math]G[/math] можно добавить ребро так, что образуются два простых цикла. Следовательно, этим деревом является [math]K_1[/math] или [math]K_2[/math]. Значит [math]G[/math] является [math]K_3 \cup K_1[/math] или [math]K_3 \cup K_2[/math], которые мы исключили из рассмотрения. Значит наш граф ацикличен. Если [math]G[/math] ациклический и [math] p = q + 1 [/math], то из [math] 4 \Rightarrow 5 [/math] и [math] 5 \Rightarrow 6 [/math] верно, что [math]G[/math] — связен. В итоге получаем, что [math]G[/math] является деревом по определению.

См. также

• Алгоритмы на деревьях
• Двоичное дерево поиска

Источники информации

• Харари Ф. Теория графов. /пер. с англ. — изд. 2-е — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
• Википедия — дерево(теория графов)