Двойственный граф планарного графа — различия между версиями
Lehanyich (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
{{Определение | {{Определение | ||
|neat=neat | |neat=neat | ||
Версия 07:56, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
- Вершины соответствуют граням .
- Между двумя вершинами в есть ребро тогда и только тогда, когда соответствующие грани в имеют общее ребро.
Чтобы для данного плоского графа построить двойственный , необходимо поместить по вершине в каждую грань (включая внешнюю), а затем, если две грани в имеют общее ребро, соединить ребром соответствующие им вершины в (если грани имеют несколько общих рёбер, соответствующие вершины следует соединить несколькими параллельными рёбрами). В результате всегда получится плоский псевдограф.
Например, существуют графы, двойственные себе: — и . Далее мы убедимся, что среди полных графов только они обладают таким свойством.
Свойства
- Если — двойственный к двусвязному графу , то — двойственный к .
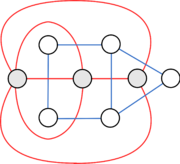
- У одного и того же графа может быть несколько двойственных, в зависимости от конкретной укладки (см. картинку).
- Поскольку любой трёхсвязный планарный граф допускает только одну укладку на сфере[2], у него должен быть единственный двойственный граф.
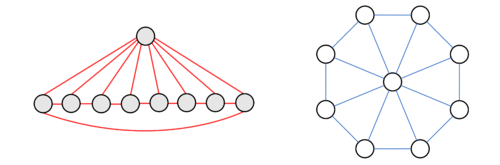
- Мост переходит в петлю, а петля — в мост. Частный случай: полный граф
- Мультиграф, двойственный к дереву, — цветок.
Самодвойственные графы
| Определение: |
| Планарный граф называется самодвойственным (англ. self-dual graph), если он изоморфен своему двойственному графу. |
Поскольку грани графа переходят в вершины, количество вершин и граней в исходном графе должно совпадать, т.е. .
Подставив в формулу Эйлера имеем: .
В полном графе .
Получаем квадратное уравнение: .
Его решения: и .
Таким образом, чтобы полный граф был самодвойственным, в нём должна быть ровно одна или четыре вершины.
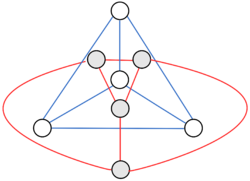
Достаточно убедиться, что два варианта укладки колеса (вершина с большой степенью внутри или вершина с большой степенью снаружи) двойственны друг другу.