Матрица смежности графа — различия между версиями
(→Оценка памяти и времени работы) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
__NOTOC__ | __NOTOC__ | ||
{{Определение | {{Определение | ||
Версия 08:18, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Определение: |
| Матрицей смежности (англ. Adjacency matrix) невзвешенного графа называется матрица , в которой — количество рёбер, соединяющих вершины и , причём при каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. |
| Определение: |
| Матрицей смежности (англ. Adjacency matrix) взвешенного графа называется матрица , в которой — вес ребра, соединяющего вершины и . |
Примеры матриц смежности:
| Взвешенность графа | Вид графа | Матрица смежности |
|---|---|---|
| Не взвешенный граф | 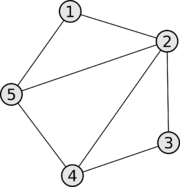
|
|
| Взвешенный граф | 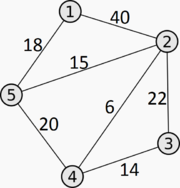
|
Оценка памяти и времени работы
Матрица смежности занимает памяти. За можно определить вес ребра или его наличие между любыми двумя вершинами. Такой способ хранения графа хорошо подходит для плотных графов, в которых число рёбер между различными парами вершин .
Свойства
| Утверждение: |
Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц). |
| Утверждение: |
Для графов без петель и кратных рёбер главная диагональ матрицы смежности целиком состоит из нулей. |
| Утверждение (о сумме элементов строки матрицы смежности для ориентированного графа): |
Сумма элементов -й строки равна , то есть .
Аналогично сумма элементов -го стоблца равна , то есть . |
| Утверждение (о сумме элементов строки матрицы смежности для неориентированного графа): |
Матрица смежности является симметричной. |
| Сумма элементов -й строки равна , то есть . Вследствие симметричности суммы элементов -й строки и -го столбца равны. |
| Теорема (о поиске количества путей заданной длины с помощью матрицы смежности ориентированного графа): |
Пусть — матрица смежности ориентированного графа без петель и , где . Тогда равно количеству путей длины . |
| Доказательство: |
|
Утверждение очевидно при . Пусть , и утверждение верно для . Тогда , где равно количеству путей длины . Следовательно, |
См. также
Источники информации
- Харари Фрэнк Теория графов Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5