Теорема Холла — различия между версиями
(см также) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
| + | |||
==Определения== | ==Определения== | ||
Версия 08:40, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Содержание
Определения
Пусть — двудольный граф.[1] — множество вершин левой доли. — множество вершин правой доли.
| Определение: |
| Полным (совершенным) паросочетанием (англ. perfect matching) называется паросочетание, в которое входят все вершины. |
| Определение: |
| Пусть . Множeство соседей (англ. neighborhood) определим формулой: |
Теорема
| Теорема (Холл [2]): |
Полное паросочетание существует тогда и только тогда, когда для любого выполнено . |
| Доказательство: |
|
База индукции Вершина из соединена хотя бы с одной вершиной из . Следовательно база верна. Индукционный переход Пусть после шагов построено паросочетание . Докажем, что в можно добавить вершину из , не насыщенную паросочетанием . Рассмотрим множество вершин — все вершины, достижимые из , если можно ходить из в только по ребрам из , а из в по любым ребрам из . Тогда в найдется вершина из , не насыщенная паросочетанием , иначе, если рассмотреть вершины (вершины из принадлежащие ), то для них не будет выполнено условие: . Тогда существует путь из в , который будет удлиняющим для паросочетания (т.к из в мы проходили по ребрам паросочетания ). Увеличив паросочетание вдоль этого пути, получаем искомое паросочетание. Следовательно предположение индукции верно. |
Пояснения к доказательству
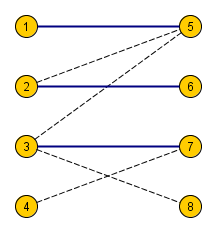
Пусть было построено паросочетание размером (синие ребра).
Добавляем вершину с номером .
Во множество вошли вершины с номерами , , , , , .
Ненасыщенная вершина из правой доли всегда найдется (в примере вершина с номером ), т.к иначе получаем противоречие:
- В входят только насыщенные вершины.
- В по крайней мере вершин (соседи по паросочетанию для каждой вершины из и ещё одна вершина, которую пытаемся добавить).
Цепь является удлиняющей для текущего паросочетания.
Увеличив текущее парасочетание вдоль этой цепи, мы насытим вершину с номером .
См. также
- Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях
- Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах
- Связь вершинного покрытия и независимого множества