Предикат "левый поворот" — различия между версиями
(→Bounding box) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
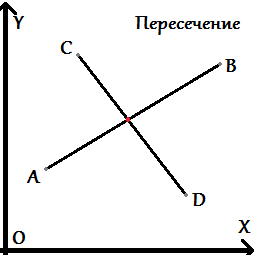
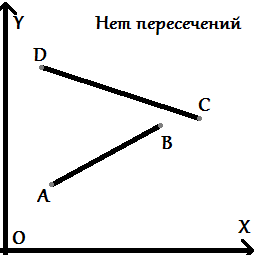
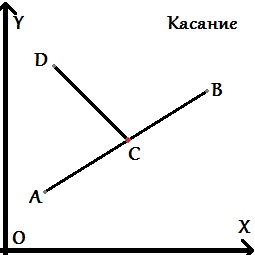
Даны два отрезка, которые задаются начальной и конечной точками <tex>a,b\ \mathcal{2}\ \mathbb R^2</tex> и определяются как множества точек <tex>s\ =\ \{(1-t)a + tb,\ t\ \in [0;1]\}</tex>. Требуется проверить существование множества их общих точек. Для определения этого факта в вычислительной геометрии используется предикат ''левый поворот'' (или ''по часовой стрелке''). | Даны два отрезка, которые задаются начальной и конечной точками <tex>a,b\ \mathcal{2}\ \mathbb R^2</tex> и определяются как множества точек <tex>s\ =\ \{(1-t)a + tb,\ t\ \in [0;1]\}</tex>. Требуется проверить существование множества их общих точек. Для определения этого факта в вычислительной геометрии используется предикат ''левый поворот'' (или ''по часовой стрелке''). | ||
Рассмотрим возможные расположения точек и самих отрезков относительно друг друга: | Рассмотрим возможные расположения точек и самих отрезков относительно друг друга: | ||
Версия 08:57, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Даны два отрезка, которые задаются начальной и конечной точками и определяются как множества точек . Требуется проверить существование множества их общих точек. Для определения этого факта в вычислительной геометрии используется предикат левый поворот (или по часовой стрелке). Рассмотрим возможные расположения точек и самих отрезков относительно друг друга:
Определим, лежат ли точки концов отрезков по разные стороны от другого отрезка.
| Определение: |
Распишем подробнее:
Какие при этом у нас будут погрешности? Допустим, что все числа положительные и будем писать без модулей:
Замечание: при сложении складываются абсолютные погрешности, при умножении складываются относительные погрешности.
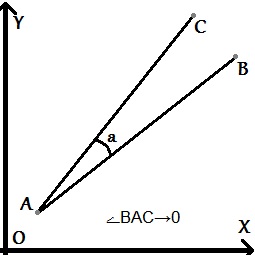
Именно поэтому, когда угол между отрезками АВ и АС крайне мал, мы можем получить неверное значение предиката.
Заметим, что все координаты (а, значит, и наши вычисления) производятся в вещественных числах, а это значит, что при вычислениях мы можем допустить ошибку. Распишем вещественное исчисление:
;
Получим некую окрестность , если ноль попадает в наш интервал, то приходится пользоваться более тяжелой артиллерией, такими как adaptive precision arithmetic, либо интервальная арифметика. Во второй, исходные переменные будут вырожденными интервалами. Из-за погрешностей, возникающих при округлении вещественных чисел, истинные значения операций нам будут неизвестны, но они обязательно будет содержаться в посчитанных интервалах.
Замечание: расписанное неравенство смотрите в другом конспекте
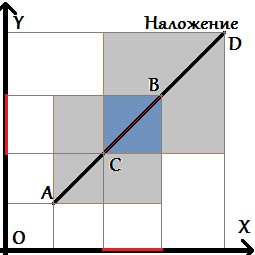
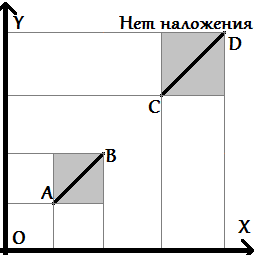
Bounding box
Ещё следует обратить внимание на граничные случаи, когда какие-то точки попадают на саму прямую. При этом возникает единственный особый случай, когда вышеописанные проверки ничего не дадут — случай, когда оба отрезка лежат на одной прямой. Этот случай рассматривается отдельно. Для этого достаточно проверить, что проекции этих двух отрезков на оси X и Y пересекаются (часто эту проверку называют проверкой на bounding box). Но отметим, что чаще всего данный предикат используют для трех точек, где одна из них относится сразу к двум отрезкам.