Рёберное ядро — различия между версиями
Vsklamm (обсуждение | вклад) (→Критерий существования реберного ядра) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
{{Определение| | {{Определение| | ||
definition= | definition= | ||
Версия 09:21, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Определение: |
| Рёберное ядро (англ. core) графа — это подграф графа , порожденный объединением таких независимых множеств , что , где — число вершинного покрытия. |
| Определение: |
| Множество ребер (вершин) называется независимым (англ. independent), если никакие его два элемента не смежны. |
| Определение: |
| Вершинным покрытием (англ. vertex cover) графа называется такое множество его вершин, что у любого ребра в хотя бы одна из вершин лежит в . |
| Определение: |
| Числом вершинного покрытия (англ. point-covering number) называется число вершин в наименьшем вершинном покрытии графа . |
Содержание
Критерий существования реберного ядра
| Определение: |
| Наименьшее вершинное покрытие графа с множеством вершин называется внешним (англ. external vertex cover), если для любого подмножества выполняется неравенство , где . |
| Теорема: |
Для произвольного графа следующие утверждения эквивалентны:
(1) имеет не пустое рёберное ядро. |
| Доказательство: |
|
Обозначим минимальное вершинное покрытие как . Пусть . |
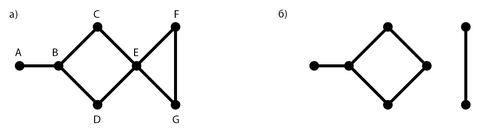
В качестве примера рассмотрим граф изображенный на рис. 1 а). Этот граф имеет два наименьших вершинных покрытия: и .
Пусть то . Пусть . Тогда .
Отсюда и . И это верно для любого подмножества . Значит, — внешнее покрытие. Значит и — внешнее покрытие.
Реберное ядро в двудольном графе
Здесь и далее будем рассматривать двудольный граф , в котором обозначим — множество вершин левой доли, — множество вершин правой доли.
| Определение: |
| — полунесводимый граф (англ. semi-irreducible graph), если имеет ровно одно вершинное покрытие , такое что или или — пусто |
| Определение: |
| — несводимый граф (англ. irreducible graph), если он имеет ровно два наименьших вершинных покрытия и , таких что либо , либо |
| Определение: |
| — сводимый граф (англ. reducible graph) если он не является ни полунесводимым, ни несводимым. |
| Теорема: |
Если оба конца ребра покрыто некоторым минимальным вершинным покрытием, то . |
| Доказательство: |
| Сошлемся на теорему 3 (Theorem 3)[1] аналогичного результата для двудольных графов. То же самое доказательство можно перенести на произвольный граф. |
| Утверждение (Следствие 1): |
Eсли имеет минимальное вершинное покрытие, которое не является независимым, то . |
| Утверждение (Следствие 2): |
Если — сводимый связный двудольный граф, то . |
| Теорема: |
Если имеет непустое реберное ядро, то , , а компоненты являются несводимыми или полунесводимыми двудольными подграфами |
| Теорема: |
и его реберное ядро совпадают тогда и только тогда, когда является двудольным и не является сводимым. |
Примеры
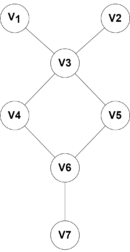
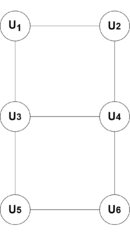
Рассмотрим двудольные графы и , изображенные на рисунках 1 и 2. В графе пусть и . Этот граф имеет единственное наименьшее вершинное покрытие и, поскольку , он полунесводимый; следовательно, он совпадает со своим рёберным ядром. В графе пусть и . В нём два наименьших вершинных покрытия, именно и . Так как и , то — несводимый граф и, значит, совпадает со своим рёберным ядром.
См. также
- NP-полнота задачи о независимом множестве
- Теория Рамсея
- Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах
Примечания
- ↑ A. L. Dulmage and N. S. Mendelsohn, 1958, pp. 519.