B+-дерево — различия между версиями
Mervap (обсуждение | вклад) |
(Отмена правки 84045, сделанной 185.220.100.252 (обсуждение)) |
||
| (не показано 40 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''' | + | '''<tex>B^{+}</tex>-дерево''' (англ. ''<tex>B^{+}</tex>-tree'') {{---}} структура данных на основе [[B-дерево|B-дерева]], сбалансированное <tex>n</tex>-арное дерево поиска с переменным, но зачастую большим количеством потомков в узле. <tex>B^{+}</tex>-деревья имеют очень высокий коэффициент ветвления (число указателей из родительского узла на дочерние, обычно порядка <tex>100</tex> или более), что снижает количество операций ввода-вывода, требующих поиска элемента в дереве. |
| − | |||
| − | |||
| − | |||
== Отличия от B-дерева == | == Отличия от B-дерева == | ||
| − | В B-дереве во всех вершинах хранятся ключи вместе с сопутствующей информацией. В | + | В <tex>B</tex>-дереве во всех вершинах хранятся ключи вместе с сопутствующей информацией. В <tex>B^{+}</tex>-деревьях вся информация хранится в листьях, а во внутренних узлах хранятся только копии ключей. Таким образом удается получить максимально возможную степень ветвления во внутренних узлах. Кроме того, листовой узел может включать в себя указатель на следующий листовой узел для ускорения последовательного доступа, что решает одну из главных проблем <tex>B</tex>-деревьев. |
| − | == Структура | + | == Структура == |
| − | Свойства | + | Свойства <tex>B^{+}</tex> дерева аналогичны [[B-дерево#Структура| свойствам <tex>B</tex>-дерева]] (с учетом отличий описанных выше). |
=== Структура узла === | === Структура узла === | ||
'''struct''' Node | '''struct''' Node | ||
| − | '''bool''' leaf <span style="color:#008000"> | + | '''bool''' leaf <span style="color:#008000"> // является ли узел листом</span> |
| − | '''int''' | + | '''int''' key_num <span style="color:#008000"> // количество ключей узла</span> |
| − | '''int''' key[] <span style="color:#008000"> | + | '''int''' key[] <span style="color:#008000"> // ключи узла</span> |
| − | '''Node''' | + | '''Node''' parent <span style="color:#008000"> // указатель на отца</span> |
| − | '''Node''' | + | '''Node''' child[] <span style="color:#008000"> // указатели на детей узла</span> |
| + | '''Info''' pointers[] <span style="color:#008000">// если лист {{---}} указатели на данные</span> | ||
| + | '''Node''' left<span style="color:#008000"> // указатель на левого брата</span> | ||
| + | '''Node''' right <span style="color:#008000"> // указатель на правого брата</span> | ||
=== Структура дерева === | === Структура дерева === | ||
| − | '''struct''' | + | '''struct''' BPlusTree |
| − | '''int''' t <span style="color:#008000"> | + | '''int''' t <span style="color:#008000"> // минимальная степень дерева</span> |
| − | '''Node''' root <span style="color:#008000"> | + | '''Node''' root <span style="color:#008000"> // указатель на корень дерева</span> |
| + | |||
| + | == Оценка высоты дерева == | ||
| + | {{Теорема|statement=Если <tex>n \geqslant 1</tex>, то для <tex>B^{+}</tex>-дерева c <tex>n</tex> узлами и минимальной степенью <tex>t \geqslant 2</tex> высота | ||
| + | :<tex>h \leqslant \log_t\dfrac{n}{2} + 1</tex> | ||
| + | |proof= | ||
| + | Так как <tex>n \geqslant 1</tex>, то корень <tex>B^{+}</tex>-дерева <tex>T</tex> содержит хотя бы один ключ, а все остальные узлы — хотя бы <tex>t - 1</tex> ключей. <tex>T</tex> имеет хотя бы <tex>2</tex> узла на высоте <tex>1</tex>, не менее <tex>2t</tex> узлов на глубине <tex>2</tex>, и так далее. То есть на глубине <tex>h</tex>, оно имеет хотя бы <tex>2t^{h-1}</tex> узлов. Так как сами ключи хранятся только в листах, а во внутренних вершинах лишь их копии, то для <tex>n</tex> ключей | ||
| + | <tex>n \geqslant 2t^{h-1}</tex> | ||
| + | |||
| + | :<tex>t^{h-1} \leqslant \dfrac{n}{2}</tex> | ||
| + | |||
| + | :<tex>h-1 \leqslant \log_t\dfrac{n}{2}</tex> | ||
| + | |||
| + | :<tex>h \leqslant \log_t\dfrac{n}{2} + 1</tex> | ||
| + | }} | ||
| + | |||
| + | Как можно заметить, высота <tex>B^{+}</tex>-дерева не более чем на <tex>1</tex> отличается от [[B-дерево#Высота|высоты <tex>B</tex>-дерева]], то есть хранение информации только в листах почти не ухудшает эффективность дерева | ||
| + | |||
| + | == Операции == | ||
| + | <tex>B^{+}</tex>-деревья являются сбалансированными, поэтому время выполнения стандартных операций в них пропорционально высоте, то есть <tex>O(\log n)</tex>. Однако стоит заметить, что так как степень дерева зачастую выбирается большой, константа при выполнении операций тоже большая. Это связано с большим количеством ключей в узлах, которые необходимо сравнить. Но из-за небольшой высоты дерева это не сильно сказывается на скорости работы. | ||
| + | |||
| + | === Поиск листа === | ||
| + | Напишем вспомогательную функцию, которая будет возвращать лист, в котором должен находится переданный ей ключ. Определяем интервал и переходим к соответствующему сыну. Повторяем пока не дошли до листа. | ||
| + | |||
| + | '''Node''' find_leaf(T: '''BPlusTree''', key: '''int'''): | ||
| + | cur = T.root | ||
| + | '''while''' cur.leaf <tex>\neq</tex> true | ||
| + | '''for''' i = 0 '''to''' cur.key_num | ||
| + | '''if''' i == cur.key_num '''or''' key < cur.key[i] | ||
| + | cur = cur.child[i] | ||
| + | '''break''' | ||
| + | '''return''' cur | ||
| + | === Поиск === | ||
| + | Находим нужный лист через <tex>find</tex>_<tex>leaf</tex> и ищем нужный ключ в нем | ||
| + | |||
| + | === Добавление ключа === | ||
| + | Ищем лист, в который можно добавить ключ и добавляем его в список ключей. Если узел не заполнен, то добавление завершено. Иначе разбиваем узел на два узла. Будем считать, что в дереве не может находиться <tex>2</tex> одинаковых ключа, поэтому <tex>insert</tex> будет возвращать был ли добавлен ключ. | ||
| + | |||
| + | '''bool''' insert(T: '''BPlusTree''', key: '''int''', value: '''Info'''): | ||
| + | leaf = find_key(T, key) | ||
| + | '''if''' key <tex>\in</tex> leaf | ||
| + | '''return false''' | ||
| + | |||
| + | <span style="color:#008000">// Ищем позицию для нового ключа </span> | ||
| + | pos = 0 | ||
| + | '''while''' pos < leaf.key_num '''and''' leaf.key[pos] < key | ||
| + | ++pos | ||
| + | |||
| + | <span style="color:#008000">// Вставляем ключ</span> | ||
| + | '''for''' i = leaf.key_num '''downto''' pos + 1 | ||
| + | leaf.key[i] = leaf.key[i - 1] | ||
| + | leaf.pointers[i] = leaf.pointer[i - 1] | ||
| + | leaf.key[pos] = key | ||
| + | leaf.pointers[pos] = value | ||
| + | ++leaf.key_num | ||
| + | |||
| + | '''if''' leaf.key_num == 2 * t <span style="color:#008000"> // t {{---}} степень дерева</span> | ||
| + | split(T, leaf) <span style="color:#008000"> // Разбиваем узел</span> | ||
| + | '''return true''' | ||
| + | |||
| + | === Разбиение узла === | ||
| + | Разбиение на два узла происходит следующим образом: в первый добавляем первые <tex>t</tex> ключей, во второй последние <tex>t - 1</tex>. Если узел {{---}} лист, то оставшийся ключ также добавляется в правое поддерево, а его копия отправляется в родительский узел, где становится разделительной точкой для двух новых поддеревьев. | ||
| + | |||
| + | Если и родительский узел заполнен {{---}} поступаем аналогично, но не копируем, а просто перемещаем оставшийся перемещаем ключ в родительский узел, так как это просто копия. Повторяем пока не встретим незаполненный узел или не дойдем до корня. В последнем случае корень разбивается на два узла и высота дерева увеличивается. | ||
| + | |||
| + | Поскольку в родителя всегда отправляется минимальный ключ из второй половины, то каждый ключ, который хранится во внутренней вершине {{---}} это минимум правого поддерева для этого ключа. | ||
| + | |||
| + | [[Файл:B Plus tree insetring.png|1000px]] | ||
| + | |||
| + | |||
| + | '''void''' split(T: '''BPlusTree''', node: '''Node'''): | ||
| + | new_node = new_Node() <span style="color:#008000"> //Создаем новый узел</span> | ||
| + | |||
| + | <span style="color:#008000">// Перенаправляем right и left указатели</span> | ||
| + | new_node.right = node.right | ||
| + | node.right.left = new_node | ||
| + | node.right = new_node | ||
| + | new_node.left = node | ||
| + | |||
| + | <span style="color:#008000">// Перемещаем t - 1 значений и соответствующих им указателей в new_node</span> | ||
| + | mid_key = node.key[t] | ||
| + | new_node.key_num = t - 1 | ||
| + | node.key_num = t | ||
| + | '''for''' i = 0 '''to''' new_node.key_num - 1 | ||
| + | new_node.key[i] = node.key[i + t + 1] | ||
| + | new_node.pointers[i] = node.pointers[i + t + 1] | ||
| + | new_node.child[i] = node.child[i + t + 1] | ||
| + | new_node.child[new_node.key_num] = node.child[2 * t] | ||
| + | |||
| + | '''if''' node.leaf | ||
| + | ++new_node.key_num | ||
| + | new_node.leaf = '''true''' | ||
| + | |||
| + | <span style="color:#008000">// Перемещаем в new_node оставшийся при разбиении элемент mid_key </span> | ||
| + | '''for''' i = new_node.key_num - 1 '''downto''' 1 | ||
| + | new_node.key[i] = new_node.key[i - 1] | ||
| + | new_node.pointers[i] = new_node.pointers[i - 1] | ||
| + | new_node.key[0] = node.key[t] | ||
| + | new_node.pointers[0] = node.pointers[t] | ||
| + | |||
| + | '''if''' node == T.root | ||
| + | T.root = new_Node() <span style="color:#008000"> // Создаем новый корень T.root </span> | ||
| + | T.root.key[0] = mid_key | ||
| + | T.root.child[0] = node | ||
| + | T.root.child[1] = new_node | ||
| + | T.root.key_num = 1; | ||
| + | node.parent = T.root | ||
| + | new_node.parent = T.root | ||
| + | '''else''' | ||
| + | new_node.parent = node.parent | ||
| + | parent = node.parent | ||
| + | |||
| + | <span style="color:#008000">// Ищем позицию mid_key в отце </span> | ||
| + | pos = 0 | ||
| + | '''while''' pos < parent.key_num '''and''' parent.key[pos] < mid_key | ||
| + | ++pos | ||
| + | |||
| + | <span style="color:#008000">// Добавляем mid_key в отца и направляем ссылку из него на new_node </span> | ||
| + | '''for''' i = parent.key_num '''downto''' pos + 1 | ||
| + | parent.key[i] = parent.key[i - 1] | ||
| + | '''for''' i = parent.key_num + 1 '''downto''' pos + 2 | ||
| + | parent.child[i] = parent.child[i - 1] | ||
| + | parent.key[pos] = mid_key | ||
| + | parent.child[pos + 1] = new_node | ||
| + | ++parent.key_num | ||
| + | |||
| + | '''if''' parent.key_num == 2 * t | ||
| + | split(T, parent) | ||
| + | |||
| + | === Удаление === | ||
| + | Поскольку все ключи находятся в листах, для удаления в первую очередь необходимо найти листовой узел, в котором он находится. Если узел содержит не менее <tex>t - 1</tex> ключей, где <tex>t</tex> {{---}} это степень дерева, то удаление завершено. Иначе необходимо выполнить попытку перераспределения элементов, то есть добавить в узел элемент из левого или правого брата (не забыв обновить информацию в родителе). Если это невозможно, необходимо выполнить слияние с братом и удалить ключ, который указывает на удалённый узел. Объединение может распространяться на корень, тогда происходит уменьшение высоты дерева. Так как мы считаем, что в дереве не может находиться <tex>2</tex> одинаковых ключей, то <tex>delete</tex> будет возвращать был ли удален ключ. | ||
| + | |||
| + | [[Файл:B-Tree-Deletions.gif]] | ||
| + | |||
| + | '''bool''' delete(T: '''BPlusTree''', key: '''int'''): | ||
| + | leaf = find_key(T, key) | ||
| + | pos = 0 | ||
| + | '''if''' key <tex>\notin</tex> leaf | ||
| + | '''return false''' | ||
| + | '''else''' | ||
| + | delete_in_node(leaf, key) <span style="color:#008000"> // Удалить ключ из вершины</span> | ||
| + | '''return true''' | ||
| + | |||
| + | '''void''' delete_in_node(tec: '''Node''', key: '''int'''): | ||
| + | '''if''' key <tex>\notin</tex> tec | ||
| + | '''return''' | ||
| + | |||
| + | <span style="color:#008000">// Ищем позицию удаляемого ключа </span> | ||
| + | pos = 0 | ||
| + | '''while''' pos < tec.key_num '''and''' tec.key[pos] < key | ||
| + | ++pos | ||
| + | |||
| + | <span style="color:#008000">// Удаляем ключ</span> | ||
| + | '''for''' i = pos '''to''' tec.key_num - 1 | ||
| + | tec.key[i] = tec.key[i + 1] | ||
| + | tec.pointers[i] = tec.pointer[i + 1] | ||
| + | '''for''' i = pos + 1 '''to''' tec.key_num | ||
| + | tec.child[i] = tec.child[i + 1] | ||
| + | --tec.key_num | ||
| + | |||
| + | '''if''' leaf.key_num < t - 1 | ||
| + | right_sibling = tec.right | ||
| + | left_sibling = tec.left | ||
| + | '''if''' left_sibling <tex>\neq</tex> null '''and''' left_sibling.key_num > t - 1 | ||
| + | --left_sibling.key_num | ||
| + | ++tec.key_num | ||
| + | |||
| + | <span style="color:#008000">// Перемещаем максимальный из left_sibling ключ на первую позицию в tec </span> | ||
| + | '''for''' i = 1 '''to''' tec.key_num - 1 | ||
| + | tec.key[i] = tec.key[i - 1] | ||
| + | tec.pointers[i] = tec.pointer[i - 1] | ||
| + | tec.child[i] = tec.child[i - 1] | ||
| + | tec.child[tec.key_num] = tec.child[tec.key_num - 1] | ||
| + | tec.key[0] = left_sibling.key[left_sibling.key_num] | ||
| + | tec.pointers[0] = left_sibling.pointers[left_sibling.key_num] | ||
| + | tec.child[0] = left_sibling.child [left_sibling.key_num + 1] | ||
| + | |||
| + | update(tec) <span style="color:#008000"> // Обновить ключи на пути к корню</span> | ||
| + | |||
| + | '''else if''' right_sibling <tex>\neq</tex> null '''and''' right_sibling.key_num > t - 1 | ||
| + | --right_sibling.key_num | ||
| + | ++tec.key_num | ||
| + | |||
| + | <span style="color:#008000">// Перемещаем минимальный из right_sibling ключ на последнюю позицию в tec </span> | ||
| + | tec.key[tec.key_num - 1] = right_sibling.key[0] | ||
| + | tec.pointers[tec.key_num - 1] = right_sibling.child[0] | ||
| + | tec.child[tec.key_num - 1] = right_sibling.pointers[0] | ||
| + | |||
| + | update(tec) <span style="color:#008000"> // Обновить ключи на пути к корню</span> | ||
| + | |||
| + | '''else''' | ||
| + | '''if''' left_sibling <tex>\neq</tex> null | ||
| + | |||
| + | <span style="color:#008000">// Сливаем tec и left_sibling</span> | ||
| + | '''for''' i = 0 to tec.key_num - 1 | ||
| + | left_sibling.key[left_sibling.key_num] = tec.key[i] | ||
| + | left_sibling.pointers[left_sibling.key_num] = tec.pointers[i] | ||
| + | left_sibling.child[left_sibling.key_num + 1] = tec.child[i] | ||
| + | ++left_sibling.key_num | ||
| + | left_sibling.child[left_sibling.key_num + 1] = tec.child[tec.key_num] | ||
| + | |||
| + | <span style="color:#008000">// Перенаправляем right и left указатели</span> | ||
| + | left_sibling.right = tec.right | ||
| + | tec.right.left = left_sibling | ||
| + | |||
| + | update(left_sibling) <span style="color:#008000"> // Обновить ключи на пути к корню</span> | ||
| + | delete_in_node(left_sibling.parent, min_key(tec)) <span style="color:#008000"> // Удаляем разделительный ключ в отце</span> | ||
| + | |||
| + | '''else''' | ||
| + | |||
| + | <span style="color:#008000">// Сливаем tec и right_sibling</span> | ||
| + | '''for''' i = 0 to tec.key_num - 1 | ||
| + | tec.key[tec.key_num] = right_sibling.key[i] | ||
| + | tec.pointers[tec.key_num] = right_sibling.pointers[i] | ||
| + | tec.child[tec.key_num + 1] = right_sibling.child[i] | ||
| + | ++tec.key_num | ||
| + | tec.child[tec.key_num + 1] = right_sibling.child[right_sibling.key_num] | ||
| + | |||
| + | <span style="color:#008000">// Перенаправляем right и left указатели</span> | ||
| + | right_sibling.right.left = tec | ||
| + | tec.right = right_sibling.right | ||
| + | |||
| + | update(tec) <span style="color:#008000"> // Обновить ключи на пути к корню</span> | ||
| + | delete_in_node(tec.parent, min_key(right_sibling)) <span style="color:#008000"> // Удаляем разделительный ключ в отце</span> | ||
| + | |||
| + | '''if''' T.root.key_num == 1 | ||
| + | T.root = T.root.child[0] | ||
| + | |||
| + | == Где используется == | ||
| + | Изначально структура предназначалась для эффективного поиска в блочно-ориентированной среде хранения {{---}} в частности, для файловых систем. Структура широко применяется в таких файловых системах, как NTFS<ref>[[wikipedia:NTFS |Wikipedia {{---}} NTFS]]</ref>, ReiserFS<ref>[[wikipedia:ReiserFS |Wikipedia {{---}} ReiserFS]]</ref>, NSS<ref>[[wikipedia:Novell Storage Services |Wikipedia {{---}} NSS]]</ref>, JFS<ref>[[wikipedia:JFS (file system) |Wikipedia {{---}} JFS]]</ref>, ReFS<ref>[[wikipedia:ReFS |Wikipedia {{---}} ReFS]]</ref>. Различные реляционные системы управления базами данных, такие как Microsoft SQL Server<ref>[[wikipedia:Microsoft SQL Server|Wikipedia {{---}} Microsoft SQL Server]]</ref>, Oracle Database<ref>[[wikipedia:Oracle Database|Wikipedia {{---}} Oracle Database]]</ref>, SQLite<ref>[[wikipedia:SQLite|Wikipedia {{---}} SQLite]]</ref> используют <tex>B^{+}</tex>-деревья для табличных индексов. | ||
| + | |||
| + | == См. также == | ||
| + | * [[B-дерево]] | ||
| + | * [[2-3 дерево]] | ||
== Примeчания == | == Примeчания == | ||
<references/> | <references/> | ||
| + | |||
| + | == Источники информации == | ||
| + | * Д. Кнут «Искусство программирования. Сортировка и поиск», часть 6.2.4 | ||
| + | * [https://en.wikipedia.org/wiki/B%2B_tree Wikipedia {{---}} B Plus tree] | ||
| + | * [https://en.wikipedia.org/wiki/B-tree Wikipedia {{---}} B tree] | ||
| + | * [https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html B plus tree visualization] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Структуры данных]] | ||
| + | [[Категория: Деревья поиска]] | ||
Текущая версия на 11:24, 1 сентября 2022
-дерево (англ. -tree) — структура данных на основе B-дерева, сбалансированное -арное дерево поиска с переменным, но зачастую большим количеством потомков в узле. -деревья имеют очень высокий коэффициент ветвления (число указателей из родительского узла на дочерние, обычно порядка или более), что снижает количество операций ввода-вывода, требующих поиска элемента в дереве.
Содержание
Отличия от B-дерева
В -дереве во всех вершинах хранятся ключи вместе с сопутствующей информацией. В -деревьях вся информация хранится в листьях, а во внутренних узлах хранятся только копии ключей. Таким образом удается получить максимально возможную степень ветвления во внутренних узлах. Кроме того, листовой узел может включать в себя указатель на следующий листовой узел для ускорения последовательного доступа, что решает одну из главных проблем -деревьев.
Структура
Свойства дерева аналогичны свойствам -дерева (с учетом отличий описанных выше).
Структура узла
struct Node bool leaf // является ли узел листом int key_num // количество ключей узла int key[] // ключи узла Node parent // указатель на отца Node child[] // указатели на детей узла Info pointers[] // если лист — указатели на данные Node left // указатель на левого брата Node right // указатель на правого брата
Структура дерева
struct BPlusTree int t // минимальная степень дерева Node root // указатель на корень дерева
Оценка высоты дерева
| Теорема: |
Если , то для -дерева c узлами и минимальной степенью высота
|
| Доказательство: |
|
Так как , то корень -дерева содержит хотя бы один ключ, а все остальные узлы — хотя бы ключей. имеет хотя бы узла на высоте , не менее узлов на глубине , и так далее. То есть на глубине , оно имеет хотя бы узлов. Так как сами ключи хранятся только в листах, а во внутренних вершинах лишь их копии, то для ключей |
Как можно заметить, высота -дерева не более чем на отличается от высоты -дерева, то есть хранение информации только в листах почти не ухудшает эффективность дерева
Операции
-деревья являются сбалансированными, поэтому время выполнения стандартных операций в них пропорционально высоте, то есть . Однако стоит заметить, что так как степень дерева зачастую выбирается большой, константа при выполнении операций тоже большая. Это связано с большим количеством ключей в узлах, которые необходимо сравнить. Но из-за небольшой высоты дерева это не сильно сказывается на скорости работы.
Поиск листа
Напишем вспомогательную функцию, которая будет возвращать лист, в котором должен находится переданный ей ключ. Определяем интервал и переходим к соответствующему сыну. Повторяем пока не дошли до листа.
Node find_leaf(T: BPlusTree, key: int):
cur = T.root
while cur.leaf true
for i = 0 to cur.key_num
if i == cur.key_num or key < cur.key[i]
cur = cur.child[i]
break
return cur
Поиск
Находим нужный лист через _ и ищем нужный ключ в нем
Добавление ключа
Ищем лист, в который можно добавить ключ и добавляем его в список ключей. Если узел не заполнен, то добавление завершено. Иначе разбиваем узел на два узла. Будем считать, что в дереве не может находиться одинаковых ключа, поэтому будет возвращать был ли добавлен ключ.
bool insert(T: BPlusTree, key: int, value: Info):
leaf = find_key(T, key)
if key leaf
return false
// Ищем позицию для нового ключа
pos = 0
while pos < leaf.key_num and leaf.key[pos] < key
++pos
// Вставляем ключ
for i = leaf.key_num downto pos + 1
leaf.key[i] = leaf.key[i - 1]
leaf.pointers[i] = leaf.pointer[i - 1]
leaf.key[pos] = key
leaf.pointers[pos] = value
++leaf.key_num
if leaf.key_num == 2 * t // t — степень дерева
split(T, leaf) // Разбиваем узел
return true
Разбиение узла
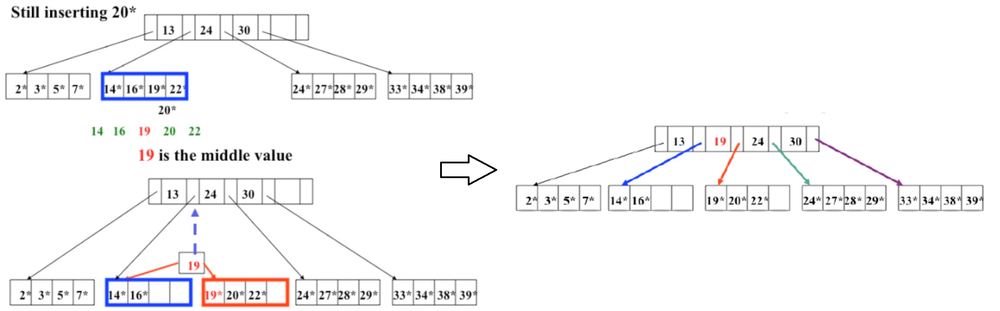
Разбиение на два узла происходит следующим образом: в первый добавляем первые ключей, во второй последние . Если узел — лист, то оставшийся ключ также добавляется в правое поддерево, а его копия отправляется в родительский узел, где становится разделительной точкой для двух новых поддеревьев.
Если и родительский узел заполнен — поступаем аналогично, но не копируем, а просто перемещаем оставшийся перемещаем ключ в родительский узел, так как это просто копия. Повторяем пока не встретим незаполненный узел или не дойдем до корня. В последнем случае корень разбивается на два узла и высота дерева увеличивается.
Поскольку в родителя всегда отправляется минимальный ключ из второй половины, то каждый ключ, который хранится во внутренней вершине — это минимум правого поддерева для этого ключа.
void split(T: BPlusTree, node: Node):
new_node = new_Node() //Создаем новый узел
// Перенаправляем right и left указатели
new_node.right = node.right
node.right.left = new_node
node.right = new_node
new_node.left = node
// Перемещаем t - 1 значений и соответствующих им указателей в new_node
mid_key = node.key[t]
new_node.key_num = t - 1
node.key_num = t
for i = 0 to new_node.key_num - 1
new_node.key[i] = node.key[i + t + 1]
new_node.pointers[i] = node.pointers[i + t + 1]
new_node.child[i] = node.child[i + t + 1]
new_node.child[new_node.key_num] = node.child[2 * t]
if node.leaf
++new_node.key_num
new_node.leaf = true
// Перемещаем в new_node оставшийся при разбиении элемент mid_key
for i = new_node.key_num - 1 downto 1
new_node.key[i] = new_node.key[i - 1]
new_node.pointers[i] = new_node.pointers[i - 1]
new_node.key[0] = node.key[t]
new_node.pointers[0] = node.pointers[t]
if node == T.root
T.root = new_Node() // Создаем новый корень T.root
T.root.key[0] = mid_key
T.root.child[0] = node
T.root.child[1] = new_node
T.root.key_num = 1;
node.parent = T.root
new_node.parent = T.root
else
new_node.parent = node.parent
parent = node.parent
// Ищем позицию mid_key в отце
pos = 0
while pos < parent.key_num and parent.key[pos] < mid_key
++pos
// Добавляем mid_key в отца и направляем ссылку из него на new_node
for i = parent.key_num downto pos + 1
parent.key[i] = parent.key[i - 1]
for i = parent.key_num + 1 downto pos + 2
parent.child[i] = parent.child[i - 1]
parent.key[pos] = mid_key
parent.child[pos + 1] = new_node
++parent.key_num
if parent.key_num == 2 * t
split(T, parent)
Удаление
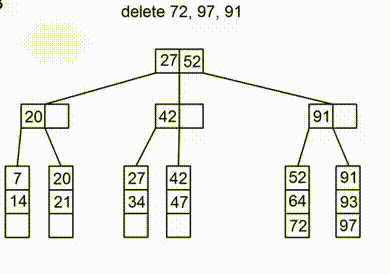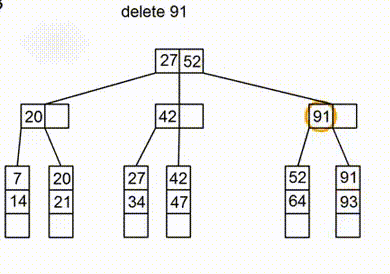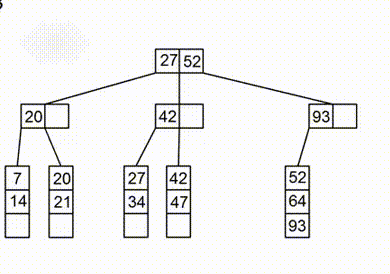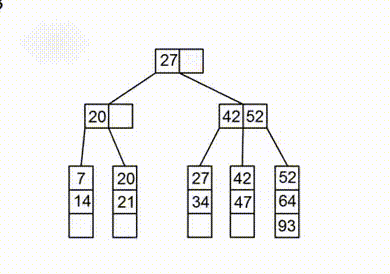
Поскольку все ключи находятся в листах, для удаления в первую очередь необходимо найти листовой узел, в котором он находится. Если узел содержит не менее ключей, где — это степень дерева, то удаление завершено. Иначе необходимо выполнить попытку перераспределения элементов, то есть добавить в узел элемент из левого или правого брата (не забыв обновить информацию в родителе). Если это невозможно, необходимо выполнить слияние с братом и удалить ключ, который указывает на удалённый узел. Объединение может распространяться на корень, тогда происходит уменьшение высоты дерева. Так как мы считаем, что в дереве не может находиться одинаковых ключей, то будет возвращать был ли удален ключ.
bool delete(T: BPlusTree, key: int):
leaf = find_key(T, key)
pos = 0
if key leaf
return false
else
delete_in_node(leaf, key) // Удалить ключ из вершины
return true
void delete_in_node(tec: Node, key: int):
if key tec
return
// Ищем позицию удаляемого ключа
pos = 0
while pos < tec.key_num and tec.key[pos] < key
++pos
// Удаляем ключ
for i = pos to tec.key_num - 1
tec.key[i] = tec.key[i + 1]
tec.pointers[i] = tec.pointer[i + 1]
for i = pos + 1 to tec.key_num
tec.child[i] = tec.child[i + 1]
--tec.key_num
if leaf.key_num < t - 1
right_sibling = tec.right
left_sibling = tec.left
if left_sibling null and left_sibling.key_num > t - 1
--left_sibling.key_num
++tec.key_num
// Перемещаем максимальный из left_sibling ключ на первую позицию в tec
for i = 1 to tec.key_num - 1
tec.key[i] = tec.key[i - 1]
tec.pointers[i] = tec.pointer[i - 1]
tec.child[i] = tec.child[i - 1]
tec.child[tec.key_num] = tec.child[tec.key_num - 1]
tec.key[0] = left_sibling.key[left_sibling.key_num]
tec.pointers[0] = left_sibling.pointers[left_sibling.key_num]
tec.child[0] = left_sibling.child [left_sibling.key_num + 1]
update(tec) // Обновить ключи на пути к корню
else if right_sibling null and right_sibling.key_num > t - 1
--right_sibling.key_num
++tec.key_num
// Перемещаем минимальный из right_sibling ключ на последнюю позицию в tec
tec.key[tec.key_num - 1] = right_sibling.key[0]
tec.pointers[tec.key_num - 1] = right_sibling.child[0]
tec.child[tec.key_num - 1] = right_sibling.pointers[0]
update(tec) // Обновить ключи на пути к корню
else
if left_sibling null
// Сливаем tec и left_sibling
for i = 0 to tec.key_num - 1
left_sibling.key[left_sibling.key_num] = tec.key[i]
left_sibling.pointers[left_sibling.key_num] = tec.pointers[i]
left_sibling.child[left_sibling.key_num + 1] = tec.child[i]
++left_sibling.key_num
left_sibling.child[left_sibling.key_num + 1] = tec.child[tec.key_num]
// Перенаправляем right и left указатели
left_sibling.right = tec.right
tec.right.left = left_sibling
update(left_sibling) // Обновить ключи на пути к корню
delete_in_node(left_sibling.parent, min_key(tec)) // Удаляем разделительный ключ в отце
else
// Сливаем tec и right_sibling
for i = 0 to tec.key_num - 1
tec.key[tec.key_num] = right_sibling.key[i]
tec.pointers[tec.key_num] = right_sibling.pointers[i]
tec.child[tec.key_num + 1] = right_sibling.child[i]
++tec.key_num
tec.child[tec.key_num + 1] = right_sibling.child[right_sibling.key_num]
// Перенаправляем right и left указатели
right_sibling.right.left = tec
tec.right = right_sibling.right
update(tec) // Обновить ключи на пути к корню
delete_in_node(tec.parent, min_key(right_sibling)) // Удаляем разделительный ключ в отце
if T.root.key_num == 1
T.root = T.root.child[0]
Где используется
Изначально структура предназначалась для эффективного поиска в блочно-ориентированной среде хранения — в частности, для файловых систем. Структура широко применяется в таких файловых системах, как NTFS[1], ReiserFS[2], NSS[3], JFS[4], ReFS[5]. Различные реляционные системы управления базами данных, такие как Microsoft SQL Server[6], Oracle Database[7], SQLite[8] используют -деревья для табличных индексов.
См. также
Примeчания
Источники информации
- Д. Кнут «Искусство программирования. Сортировка и поиск», часть 6.2.4
- Wikipedia — B Plus tree
- Wikipedia — B tree
- B plus tree visualization