1outtreesumwc — различия между версиями
Shersh (обсуждение | вклад) м (→Алгоритм) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 6 промежуточных версий 5 участников) | |||
| Строка 82: | Строка 82: | ||
L = {1, ... , n} | L = {1, ... , n} | ||
'''while''' L <tex> \ne </tex> {root} <font color=darkgreen>// пока в списке работ не останется только корень</font> | '''while''' L <tex> \ne </tex> {root} <font color=darkgreen>// пока в списке работ не останется только корень</font> | ||
| − | Найти работу j <tex> \in </tex> L с | + | Найти работу j <tex> \in </tex> L с максимальным значением q[j] |
par = P[j] | par = P[j] | ||
Найти i, что par <tex> \in </tex> J[i] | Найти i, что par <tex> \in </tex> J[i] | ||
| Строка 102: | Строка 102: | ||
[[Файл:JobsOuttrees.jpg|650px]] | [[Файл:JobsOuttrees.jpg|650px]] | ||
| − | Первой выберется работа с номером <tex> 5 </tex>. Она | + | Первой выберется работа с номером <tex> 5 </tex>. Она объединится со своим родителем <tex> 2 </tex> и допишется в конец <tex> \pi_2 </tex>. Потом выберется работа <tex> 4 </tex>, потом <tex> \{2, 5\} </tex> и т. д. Процесс будет продолжаться, пока не останется одна вершина. Ответ {{---}} оптимальная последовательность работ {{---}} содержится в <tex> \pi_1 </tex>, который написан внутри последней вершины. |
== Доказательство оптимальности алгоритма == | == Доказательство оптимальности алгоритма == | ||
| Строка 111: | Строка 111: | ||
Доказательство проведём по индукции. Очевидно, что для одной вершины алгоритм построит оптимальное расписание. Пусть теперь он может составить оптимальную последовательность назначенных работ числом меньше <tex> n </tex>. Пусть также работы <tex> i, j </tex> {{---}} работы, которые объединятся на первом шаге алгоритма. Тогда оптимальное расписание <tex> R </tex> можно представить следующим образом: | Доказательство проведём по индукции. Очевидно, что для одной вершины алгоритм построит оптимальное расписание. Пусть теперь он может составить оптимальную последовательность назначенных работ числом меньше <tex> n </tex>. Пусть также работы <tex> i, j </tex> {{---}} работы, которые объединятся на первом шаге алгоритма. Тогда оптимальное расписание <tex> R </tex> можно представить следующим образом: | ||
| − | <tex> \pi \colon \pi (1), | + | <tex> \pi \colon \pi (1), \ldots, \pi (k), i, j, \pi (k + 3), \ldots, \pi (n) </tex> |
После объединения работ <tex> i </tex> и <tex> j </tex> в одну расписание <tex> R' </tex> примет такой вид: | После объединения работ <tex> i </tex> и <tex> j </tex> в одну расписание <tex> R' </tex> примет такой вид: | ||
| − | <tex> \pi ' \colon \pi (1), | + | <tex> \pi ' \colon \pi (1), \ldots, \pi (k), I, \pi (k + 3), \ldots, \pi (n) </tex> |
где <tex> I = \{i, j\}, ~w(I) = w(i) + w(j), p(I) = p(i) + p(j)</tex>. Обозначим за <tex> f_n(\pi ), ~f_{n-1}(\pi ') </tex> целевые функции для последовательностей <tex> \pi </tex> и <tex> \pi ' </tex> соответственно. Тогда | где <tex> I = \{i, j\}, ~w(I) = w(i) + w(j), p(I) = p(i) + p(j)</tex>. Обозначим за <tex> f_n(\pi ), ~f_{n-1}(\pi ') </tex> целевые функции для последовательностей <tex> \pi </tex> и <tex> \pi ' </tex> соответственно. Тогда | ||
| Строка 125: | Строка 125: | ||
Теперь разделим обе части равенства <tex> (*) </tex> на <tex> w(i)w(j) </tex>. Получим, что расстояние между целевыми функциями равно | Теперь разделим обе части равенства <tex> (*) </tex> на <tex> w(i)w(j) </tex>. Получим, что расстояние между целевыми функциями равно | ||
| − | <tex | + | <tex> -\dfrac{p(j)}{w(j)} = -\dfrac{1}{q(j)} </tex> |
Это расстояние минимально (по модулю), так как мы выбирали работу <tex> j </tex> с максимальным значением <tex> q(j) </tex>. Из этих утверждений и следует оптимальность построенного алгоритмом расписания. | Это расстояние минимально (по модулю), так как мы выбирали работу <tex> j </tex> с максимальным значением <tex> q(j) </tex>. Из этих утверждений и следует оптимальность построенного алгоритмом расписания. | ||
| + | }} | ||
| + | |||
| + | == 1 | intree | Sum(w*C)== | ||
| + | <tex dpi="200"> 1 \mid intree \mid \sum w_i C_i </tex> | ||
| + | {{Задача | ||
| + | |definition= | ||
| + | Необходимо составить расписание на одном станке работ с произвольными временами выполнения. Минимизировать нужно взвешенную сумму времен завершения работ. Зависимости между работами заданы [[Дерево, эквивалентные определения | деревом]], в котором листья {{---}} работы, которые доступны в начале, а все остальные работы недоступны пока все их дети не будут выполнены. | ||
| + | }} | ||
| + | Сведем задачу <tex> S_{in} = 1 \mid intree \mid \sum w_i C_i </tex> к решенной задаче <tex>S_{out} = 1 \mid outtree \mid \sum w_i C_i </tex> следующим образом: | ||
| + | # Развернем все ребра: если работа <tex> i </tex> зависела от работы <tex> j </tex>, теперь работа <tex> j </tex> будет зависеть от <tex> i </tex>. | ||
| + | # Заменим все стоимости <tex> w_i </tex> на противоположные <tex> w'_i = - w_i</tex>. | ||
| + | {{Теорема | ||
| + | |statement=Развернутое оптимальное расписание соответствующей задачи <tex> S_{out} </tex> с весами <tex> w'_i </tex> является оптимальным расписанием для задачи <tex> S_{in} </tex> | ||
| + | |proof= | ||
| + | Полученное расписание будет допустимым, так как расписание для <tex> S_{out} </tex> было допустимым, и в нем никакие две работы не пересекались и не прерывались. Развернув ребра, мы не могли нарушить это свойство. Также из-за того, что мы развернули ребра в расписании, мы добились того, что все работы выполняются в правильном порядке (в расписании для <tex> S_{out} </tex> из-за того, что все ребра были развернуты, порядок был нарушен для всех работ). Таким образом получили, что расписание допустимое. | ||
| + | |||
| + | Пусть с помощью задачи <tex> S_{out} </tex> мы получили последовательность работ <tex> 1 \dots n </tex>. Распишем по определению значение целевой функции для <tex> S_{out} </tex>: | ||
| + | <tex> | ||
| + | \sum\limits_{i=1}^n \left( -w_i C_i \right) | ||
| + | = \sum \limits_{i=1}^n \left( -w_i \sum \limits_{j=1}^i p_j \right) = \\ | ||
| + | = \sum\limits_{i=1}^n \left( w_i \sum\limits_{j=i+1}^n p_j \right) | ||
| + | - \sum\limits_{i=1}^n w_i \sum \limits_{i=1}^n p_i = \\ | ||
| + | = \sum\limits_{i=1}^n \left( w_i \sum\limits_{j=i}^n p_j \right) | ||
| + | - \sum\limits_{i=1}^n w_i p_i | ||
| + | - \sum\limits_{i=1}^n w_i \sum \limits_{i=1}^n p_i | ||
| + | </tex> | ||
| + | Заметим, что первое слагаемое соответствует целевой функции <tex> \sum w_i C_i </tex> для последовательности <tex> n \dots 1 </tex>, а второе и третье слагаемые — константы, зависящие только от входных данных и не зависящие от перестановки работ. Таким образом, оптимальное значение для <tex> S_{out} </tex> также минимизирует <tex> S_{in} </tex>. | ||
}} | }} | ||
| Строка 133: | Строка 160: | ||
* P. Brucker. Scheduling Algorithms (2006), 5th edition, стр. 73 - 78 | * P. Brucker. Scheduling Algorithms (2006), 5th edition, стр. 73 - 78 | ||
| − | [[Категория: | + | [[Категория: Алгоритмы и структуры данных]] |
[[Категория: Теория расписаний]] | [[Категория: Теория расписаний]] | ||
Текущая версия на 19:03, 4 сентября 2022
| Задача: |
| Необходимо составить расписание на одном станке работ с произвольными временами выполнения. Минимизировать нужно взвешенную сумму времен завершения работ. Зависимости между работами заданы исходящим деревом — работа, которая соответствует корню, доступна в начале, все другие работы зависят от одной работы — отца в дереве. |
Тривиальным примером подобной задачи является демонтаж сложного механизма.
Содержание
Свойства оптимального расписания
Докажем некоторые свойства оптимального расписания, которые мы будем использовать в доказательстве корректности алгоритма.
Введем некоторые обозначения для удобства. За обозначим список всех ребёр дерева. Для всех работ обозначим за всех потомков в дереве зависимостей, включая саму работу , введём новый параметр работы .
Для подмножества работ определим:
Два непересекающихся множества работ будем называть параллельными , если для всех выполняется: не является ни предком, ни потомком . Если множества состоят из одной работы , будем писать . Каждое расписание представлено перестановкой .
| Лемма: |
Пусть — оптимальное расписание, и — два таких параллельных блока (множества работ, выполняемых последовательно) из , что выполняется сразу после . Пусть — расписание, полученное из перестановкой и . Тогда выполяются следующие пункты:
|
| Доказательство: |
|
|
| Теорема: |
Пусть работы такие, что — предок , и . Тогда существует оптимальное расписание, в котором работа идёт сразу после работы |
| Доказательство: |
|
Каждое расписание может быть представлено последовательностью работ в порядке, в котором они выполняются. Пусть будет оптимальной такой последовательностью. Также предположим, что количество работ между и равное было бы минимальным. Можно считать, что . Тогда расписание можно представить следующим образом: Рассмотрим случая. Случай 1:
Случай 2:
|
Алгоритм
Доказанная в предыдущем пункте теорема уже даёт основную идею алгоритма: взять работу , отличную от корня дерева, с максимальным значением и поставить её в расписании сразу после своего непосредственного предка . Так как существует оптимальное расписание, в котором работа идёт сразу после , то мы можем объедить вершины графа в одну вершину , которая представляет собой последовательность . Все сыновья работы станут сыновьями новой вершины .
Будем повторять процесс слияния вершин, пока не останется всего одна вершина.
Таким образом каждая вершина представляется множеством работ и соответствующей этому множеству последовательностью . На очередном шаге алгоритма мы находим вершину , отличную от корня, с максимальным значением . Пусть — непосредственный предок работы . Тогда нам надо найти такую вершину , что . После этого мы объединяем обе вершины, заменяя и на и , где — это конкатенация последовательностей и .
Детали описаны в алгоритме ниже, в котором
- обозначает последнюю работу в последовательности ,
- обозначает предка в графе зависимостей, а после слияния с какой-то вершиной — предыдущую работу в последовательности .
w[root] = for i = 1..n E[i] = {i} J[i] = {i} q[i] = w[i] \ p[i] L = {1, ... , n} while L {root} // пока в списке работ не останется только корень Найти работу j L с максимальным значением q[j] par = P[j] Найти i, что par J[i] w[i] += w[j] p[i] += p[j] q[i] = w[i] / w[j] // пересчитаем значения в вершине P[j] = E[i] // предком работы j теперь будет последняя работа в E[i] = E[j] // последней работой в теперь будет последняя работа в J[i] = J[i] J[j] L = L \ {j}
Вначале делаем присваивание , чтобы корень никогда не выбрался на шаге выбора вершины с максимальным значением . В реализации же можно просто дополнительно проверять на равенство с корнем, чтобы избежать переполнений или испортить значение .
После завершения этой процедуры оптимальное расписание можно восстановить с конца, зная и массив .
Если для получения работы с минимальным значением использовать очередь с приоритетами, а для поиска родителям вершины использовать систему непересекающихся множеств, то время работы алгоритма будет .
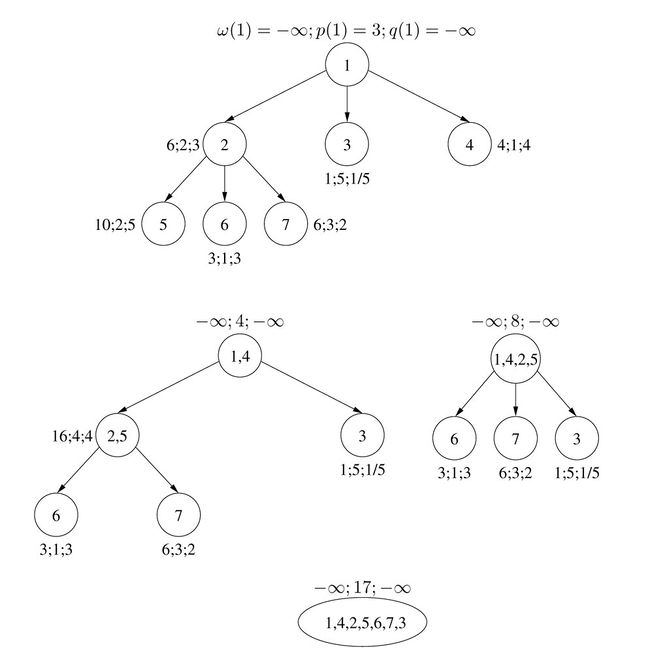
Проиллюстрируем работу алгоритма на следующем примере.
Первой выберется работа с номером . Она объединится со своим родителем и допишется в конец . Потом выберется работа , потом и т. д. Процесс будет продолжаться, пока не останется одна вершина. Ответ — оптимальная последовательность работ — содержится в , который написан внутри последней вершины.
Доказательство оптимальности алгоритма
| Теорема: |
Алгоритм строит оптимальное расписание. |
| Доказательство: |
|
Доказательство проведём по индукции. Очевидно, что для одной вершины алгоритм построит оптимальное расписание. Пусть теперь он может составить оптимальную последовательность назначенных работ числом меньше . Пусть также работы — работы, которые объединятся на первом шаге алгоритма. Тогда оптимальное расписание можно представить следующим образом:
После объединения работ и в одну расписание примет такой вид:
где . Обозначим за целевые функции для последовательностей и соответственно. Тогда
Следовательно, расписание будет оптимальным тогда и только тогда, когда расписание будет оптимальным. А по предположению индукции наш алгоритм составит оптимальное расписание для последовательности . Теперь разделим обе части равенства на . Получим, что расстояние между целевыми функциями равно Это расстояние минимально (по модулю), так как мы выбирали работу с максимальным значением . Из этих утверждений и следует оптимальность построенного алгоритмом расписания. |
1 | intree | Sum(w*C)
| Задача: |
| Необходимо составить расписание на одном станке работ с произвольными временами выполнения. Минимизировать нужно взвешенную сумму времен завершения работ. Зависимости между работами заданы деревом, в котором листья — работы, которые доступны в начале, а все остальные работы недоступны пока все их дети не будут выполнены. |
Сведем задачу к решенной задаче следующим образом:
- Развернем все ребра: если работа зависела от работы , теперь работа будет зависеть от .
- Заменим все стоимости на противоположные .
| Теорема: |
Развернутое оптимальное расписание соответствующей задачи с весами является оптимальным расписанием для задачи |
| Доказательство: |
|
Полученное расписание будет допустимым, так как расписание для было допустимым, и в нем никакие две работы не пересекались и не прерывались. Развернув ребра, мы не могли нарушить это свойство. Также из-за того, что мы развернули ребра в расписании, мы добились того, что все работы выполняются в правильном порядке (в расписании для из-за того, что все ребра были развернуты, порядок был нарушен для всех работ). Таким образом получили, что расписание допустимое. Пусть с помощью задачи мы получили последовательность работ . Распишем по определению значение целевой функции для : Заметим, что первое слагаемое соответствует целевой функции для последовательности , а второе и третье слагаемые — константы, зависящие только от входных данных и не зависящие от перестановки работ. Таким образом, оптимальное значение для также минимизирует . |
Источники информации
- P. Brucker. Scheduling Algorithms (2006), 5th edition, стр. 73 - 78