Троичный поиск — различия между версиями
Rybak (обсуждение | вклад) м (→Смотрите также) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 33 промежуточные версии 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Троичный поиск''' ( | + | '''Троичный поиск''' (''ternary search, тернарный поиск'') {{---}} метод поиска минимума или максимума функции на отрезке, которая либо сначала строго возрастает, затем строго убывает, либо наоборот. |
| − | |||
== Алгоритм == | == Алгоритм == | ||
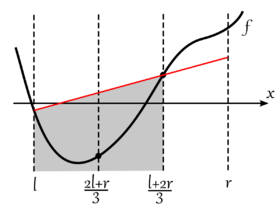
| + | [[File:Ternar2.png|thumb|280px|Пример. <tex>f(a) < f(b) \implies x_{min} \in [l, b]</tex>]] | ||
| − | + | Рассмотрим этот алгоритм на примере поиска минимума (поиск максимума аналогичен). | |
| − | Рассмотрим этот алгоритм на примере поиска минимума (поиск максимума аналогичен). | ||
Пусть функция <tex>f(x)</tex> на отрезке <tex>[l, r]</tex> имеет минимум, и мы хотим найти точку <tex>x_{min}</tex>, в которой он достигается. | Пусть функция <tex>f(x)</tex> на отрезке <tex>[l, r]</tex> имеет минимум, и мы хотим найти точку <tex>x_{min}</tex>, в которой он достигается. | ||
| − | Посчитаем значения функции в точках <tex> a = l + \ | + | Посчитаем значения функции в точках <tex> a = l + \dfrac{(r-l)}{3} </tex> и <tex> b = l + \dfrac{2(r-l)}{3} </tex>. |
Так как в точке <tex>x_{min}</tex> минимум, то на отрезке <tex>[l, x_{min}]</tex> функция убывает, а на <tex>[x_{min}, r]</tex> {{---}} возрастает, то есть | Так как в точке <tex>x_{min}</tex> минимум, то на отрезке <tex>[l, x_{min}]</tex> функция убывает, а на <tex>[x_{min}, r]</tex> {{---}} возрастает, то есть | ||
<tex> \forall x', x'' \in [l, r]: \\ | <tex> \forall x', x'' \in [l, r]: \\ | ||
| − | l < x' < x'' < x_{min} \ | + | l < x' < x'' < x_{min} \implies f(l) > f(x') > f(x'') > f(x_{min}) \\ |
| − | x_{min} < x' < x'' < r \ | + | x_{min} < x' < x'' < r \implies f(x_{min}) < f(x') < f(x'') < f(r) </tex>. |
Значит если <tex>f(a) < f(b)</tex>, то <tex>x_{min} \in [l, b]</tex>, | Значит если <tex>f(a) < f(b)</tex>, то <tex>x_{min} \in [l, b]</tex>, | ||
аналогично из <tex>f(a) > f(b)</tex> следует <tex> x_{min} \in [a, r]</tex>. | аналогично из <tex>f(a) > f(b)</tex> следует <tex> x_{min} \in [a, r]</tex>. | ||
| + | |||
Тогда нам нужно изменить границы поиска и искать дальше, | Тогда нам нужно изменить границы поиска и искать дальше, | ||
пока не будет достигнута необходимая точность, то есть <tex> r-l < \varepsilon </tex>. | пока не будет достигнута необходимая точность, то есть <tex> r-l < \varepsilon </tex>. | ||
| + | |||
| + | Из рассуждений и рисунка может возникнуть идея взять, например, отрезок <tex>[l, a]</tex> вместо отрезка <tex>[l, b]</tex>. Но этого делать нельзя, потому что мы не умеем различать случаи, когда <tex>f(a) < f(b)</tex> и <tex>a</tex> слева или справа от минимума. | ||
| + | |||
| + | Можно заметить, что если мы всегда будем брать отрезок <tex>[l, b]</tex> при <tex>f(a) < f(b)</tex> или <tex>[a, r]</tex> при <tex>f(a) > f(b)</tex> , то минимум функции всегда будет в нашем отрезке. Если <tex>f(a) = f(b)</tex>, то можно взять любой отрезок. | ||
=== Псевдокод === | === Псевдокод === | ||
| − | + | Рекурсивный вариант: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''double''' ternarySearchMin('''double''' f(), '''double''' left, '''double''' right, '''double''' eps): | |
| − | + | '''if''' right - left < eps | |
| − | ternarySearchMin(f, | + | '''return''' (left + right) / 2 |
| − | |||
| − | |||
a = (left * 2 + right) / 3 | a = (left * 2 + right) / 3 | ||
b = (left + right * 2) / 3 | b = (left + right * 2) / 3 | ||
| − | if | + | '''if''' f(a) < f(b) |
| − | + | '''return''' ternarySearchMin(f, left, b, eps) | |
| − | else | + | '''else''' |
| − | + | '''return''' ternarySearchMin(f, a, right, eps) | |
| − | + | ||
| − | + | Итеративный вариант: | |
| − | |||
| + | '''double''' ternarySearchMin('''double''' f(), '''double''' left, '''double''' right, '''double''' eps): | ||
| + | '''while''' right - left > eps | ||
| + | a = (left * 2 + right) / 3 | ||
| + | b = (left + right * 2) / 3 | ||
| + | '''if''' f(a) < f(b) | ||
| + | right = b | ||
| + | '''else''' | ||
| + | left = a | ||
| + | '''return''' (left + right) / 2 | ||
=== Время работы === | === Время работы === | ||
| Строка 55: | Строка 56: | ||
Так как на каждой итерации мы считаем два значения функции и уменьшаем область поиска в полтора раза, пока <tex> r - l > \varepsilon</tex>, | Так как на каждой итерации мы считаем два значения функции и уменьшаем область поиска в полтора раза, пока <tex> r - l > \varepsilon</tex>, | ||
то время работы алгоритма составит | то время работы алгоритма составит | ||
| − | <tex>2 \log_{\frac32} \left(\ | + | <tex dpi = "135">2 \log_{\frac32} \left(\dfrac{r - l}{\varepsilon}\right)</tex> |
| − | == | + | == См. также == |
| − | + | * [[Поиск с помощью золотого сечения]] | |
| − | + | == Источники информации == | |
| − | + | * Дональд Кнут {{---}} Искусство программирования. Том 3. Сортировка и поиск. / Knuth D.E. {{---}} The Art of Computer Programming. Vol. 3. Sorting and Searching. | |
| + | * [[wikipedia:ru:Троичный поиск|Троичный поиск — Википедия]] | ||
| + | * [[wikipedia:Ternary search|Ternary search {{---}} Wikipedia]] | ||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| + | [[Категория: Алгоритмы поиска]] | ||
Текущая версия на 19:05, 4 сентября 2022
Троичный поиск (ternary search, тернарный поиск) — метод поиска минимума или максимума функции на отрезке, которая либо сначала строго возрастает, затем строго убывает, либо наоборот.
Алгоритм
Рассмотрим этот алгоритм на примере поиска минимума (поиск максимума аналогичен).
Пусть функция на отрезке имеет минимум, и мы хотим найти точку , в которой он достигается.
Посчитаем значения функции в точках и .
Так как в точке минимум, то на отрезке функция убывает, а на — возрастает, то есть
.
Значит если , то , аналогично из следует .
Тогда нам нужно изменить границы поиска и искать дальше, пока не будет достигнута необходимая точность, то есть .
Из рассуждений и рисунка может возникнуть идея взять, например, отрезок вместо отрезка . Но этого делать нельзя, потому что мы не умеем различать случаи, когда и слева или справа от минимума.
Можно заметить, что если мы всегда будем брать отрезок при или при , то минимум функции всегда будет в нашем отрезке. Если , то можно взять любой отрезок.
Псевдокод
Рекурсивный вариант:
double ternarySearchMin(double f(), double left, double right, double eps):
if right - left < eps
return (left + right) / 2
a = (left * 2 + right) / 3
b = (left + right * 2) / 3
if f(a) < f(b)
return ternarySearchMin(f, left, b, eps)
else
return ternarySearchMin(f, a, right, eps)
Итеративный вариант:
double ternarySearchMin(double f(), double left, double right, double eps):
while right - left > eps
a = (left * 2 + right) / 3
b = (left + right * 2) / 3
if f(a) < f(b)
right = b
else
left = a
return (left + right) / 2
Время работы
Так как на каждой итерации мы считаем два значения функции и уменьшаем область поиска в полтора раза, пока , то время работы алгоритма составит
См. также
Источники информации
- Дональд Кнут — Искусство программирования. Том 3. Сортировка и поиск. / Knuth D.E. — The Art of Computer Programming. Vol. 3. Sorting and Searching.
- Троичный поиск — Википедия
- Ternary search — Wikipedia