Пересечение полуплоскостей, связь с выпуклыми оболочками — различия между версиями
(→Связь пересечения полуплоскостей с выпуклой оболочкой) |
м (rollbackEdits.php mass rollback) |
| (не показана 1 промежуточная версия 1 участника) | |
(нет различий)
| |
Текущая версия на 19:05, 4 сентября 2022
Предикат трех прямых
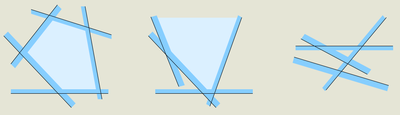
Задача: есть конечное множество полуплоскостей, найти фигуру их пересечения или сообщить что оно пусто.
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскость выпукла)
Пусть полуплоскости заданы уравнениями прямых и ориентацией, с какой стороны от прямой лежит полуплоскость.
Сначала рассмотрим все полуплоскости, которые "смотрят", то есть ориентированны, вниз. Аналогично можно рассмотреть все полуплоскости, которые ориентированны вверх.
| Лемма: |
| Доказательство: |
|
Для проверки предиката нужно определить знак выражения , где — точка пересечения прямых и . Эта точка находится из уравнения . Решением будет . Подставим это решение в и домножим на определитель.
|
Таким образом, если представить прямую как точку с однородными координатами , то этот предикат — всего лишь поворот, а проверка предиката — проверка очередной точки в обходе Грэхема для нахождения выпуклой оболочки.
Алгоритм:
- Отсортировать все полуплоскости по углу наклона;
- Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем);
- Запустить обход Грэхема для полуплоскостей, смотрящих вверх;
- Пересечь две цепочки.
От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная — когда обе цепочки не пусты и пересекаются.
Связь пересечения полуплоскостей с выпуклой оболочкой
| Лемма: |
Пересечение полуплоскостей может быть получено построением выпуклой оболочки в двойственном прострастве для множества точек, являющихся дуальным преобразованием исходных полуплоскостей |
| Доказательство: |
|
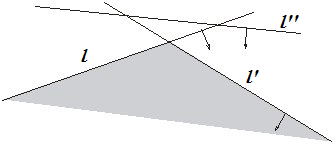
Важно: Покажем конструктивный алгоритм для множестве полуплоскостей, не содержащих вертикальный полуплоскости. После леммы приведены два рассуждения, позволяющие снять данное ограничение. Важно: В картинке перепутаны и . TODO
Пусть у нас есть множество ориентированных прямых, каждая из которых задает полуплоскость(направление вектора нормали задаёт нужную полуплоскость). Тогда каждую плоскость мы можем превратить в точку в двойственном пространстве: . Далее воспользуемся основными свойствами дуальной трансформации (см. доказательтсво в конспекте о двойственном прострастве):
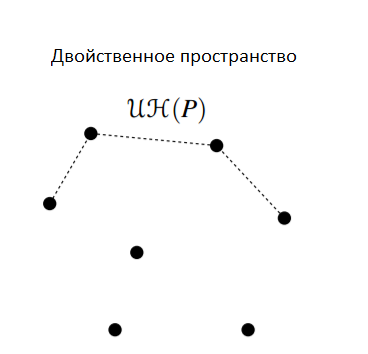
Рассмотрим множество точек() в двойственном пространстве и рассмотрим верхнюю часть выпуклой оболочки, построенной на этих точках. Обозначим её за (Upper hull). Далее мы будем работать только с прямыми(в исходном пространстве), у которых вектор нормали направлен вниз, т.е они образовывают верхнюю цепочку. По свойству выпуклой оболочки, любое ребро из цепи содержит "ниже" себя все точки множества , а так же эта цепь соединяет самую правую точку с самой левой. Рассмотрим какую-то точку и заметим, что она будет принадлежать цепи прямая : и все точки из лежат ниже (сейчаc мы жили в двойственном пространстве). В обычном пространстве данный факт эквивалентен следующему:
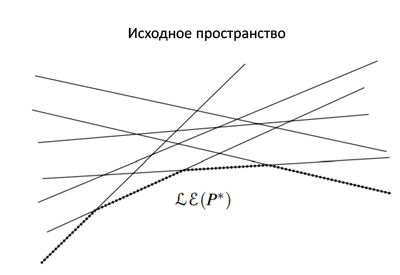
Итого: у нас есть точка на прямой , лежащая ниже всех остальных прямых из . Посмотрим на планарный граф множества(рис.2) прямых. Из факта выше, мы можем понять, что внесла ребро в самый нижний фейс(именно тот, который задаёт часть пересечения полуплоскостей). Обозначим цепочку данного фейса, как . Математически данную цепочку мы можем описать, как минимум из всех линейных функция (заданные прямыми) в . Так же компонента узлов этой цепочки монотонно возрастает. Вернемся к и заметим, что при обходе цепи, координата точек растет. Если же мы будет обходить цепочку из , образующую пересечение полуплоскостей, мы заметим, что наклон прямых уменьшается. Учитывая этот факт, и то что наклон линии из совпадет с координатой точки (вспоминаем отображение и применяем производную), можно сделать вывод, что обход слева направо точек из цепи , совпадает с обходом точек из справа налево. (Обе линии монотоны, одна возрастает, другая убывает. Количество точек в массиве одинаковое, при это каждая точка из внесла вклад в ) Напоследок, cоседние точки и из образуют какое-то или принадлежат какому-то ребру все точки из лежат "ниже" линии, построенной на точках и . В исходном пространстве это означает: все прямые из пространства за исключением прямых и лежат над пересечением и . Это достаточное условие, что пересечение и . Таким образом мы построили верхнее пересечение полуплоскостей. Аналогичным образом строится нижнее, затем мы пересекаем полученные две цепочки. |
Что же делать с вертикальными линиями?
- Найдем все вертикальным прямые за . Возьмем самую правую, у которой нормаль смотрит вправо, и самую левую, у которых нормаль смотрит влево. Построим верхнюю цепь и нижнюю цепь без всех вертикальных прямых, затем пересечем верхнюю цепь, нижнюю цепь, самую правую и самую левую вертикальную прямую.
- Перейдем в однородное двойственное пространство.
Источники
- http://wwwisg.cs.uni-magdeburg.de/ag/lehre/SS2012/GAG/slides/V12.pdf
- Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 11 page 253-254