Сжатое многомерное дерево отрезков — различия между версиями
(→Псевдокод) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 3 промежуточные версии 2 участников) | |||
| Строка 6: | Строка 6: | ||
==Оптимизация== | ==Оптимизация== | ||
| − | Для уменьшения количества занимаемой памяти можно провести оптимизацию <tex>p</tex>-мерного дерева отрезков. Для начала, будем использовать дерево отрезков с сохранением всего подотрезка в каждой вершине. Другими словами, в каждой вершине дерева отрезков мы будем хранить не только какую-то сжатую информацию об этом подотрезке, но и все элементы множества <tex>A</tex>, лежащие в этом подотрезке. На первый взгляд, это только увеличит объем структуры, но не все так просто. При построении будем действовать следующим образом — каждый раз дерево отрезков внутри вершины будем строить не по всем элементам множества <tex>A</tex>, а только по сохраненному в этой вершине подотрезку. Действительно, незачем строить дерево по всем элементам, когда элементы вне подотрезка уже были «исключены» и заведомо лежат вне желаемого <tex>p</tex>-мерного прямоугольника. Такое «усеченное» многомерное дерево отрезков называется '''сжатым'''. | + | Для уменьшения количества занимаемой памяти можно провести оптимизацию <tex>p</tex>-мерного дерева отрезков. Для начала, будем использовать дерево отрезков с сохранением всего подотрезка в каждой вершине. Другими словами, в каждой вершине дерева отрезков мы будем хранить не только какую-то сжатую информацию об этом подотрезке, но и все элементы множества <tex>A</tex>, лежащие в этом подотрезке. На первый взгляд, это только увеличит объем структуры, но не все так просто. При построении будем действовать следующим образом — каждый раз дерево отрезков внутри вершины будем строить не по всем элементам множества <tex>A</tex>, а только по сохраненному в этой вершине подотрезку. Действительно, незачем строить дерево по всем элементам, когда элементы вне подотрезка уже были «исключены» и заведомо лежат вне желаемого <tex>p</tex>-мерного прямоугольника. Такое «усеченное» многомерное дерево отрезков называется '''сжатым''' (англ. ''compressed''). |
==Построение дерева== | ==Построение дерева== | ||
| − | Рассмотрим алгоритм построения сжатого дерева отрезков на | + | Рассмотрим алгоритм построения сжатого дерева отрезков на примере множества <tex>A</tex>, состоящего из <tex>4</tex>-х взвешенных точек в <tex>2</tex>-мерном пространстве (плоскости):<br> |
<tex> | <tex> | ||
| − | p=2, | + | p=2,~~n=4,~~A: |
\begin{cases} | \begin{cases} | ||
(1, 3), \mbox{weight}=7 \\ | (1, 3), \mbox{weight}=7 \\ | ||
Текущая версия на 19:07, 4 сентября 2022
| Задача: |
| Пусть имеется множество , состоящее из взвешенных точек в -мерном пространстве. Необходимо быстро отвечать на запрос о суммарном весе точек, находящихся в -мерном прямоугольнике |
Вообще говоря, с поставленной задачей справится и обычное -мерное дерево отрезков. Для этого достаточно на -том уровне вложенности строить дерево отрезков по всевозможным -тым координатам точек множества , а при запросе использовать на каждом уровне бинарный поиск для установления желаемого подотрезка. Очевидно, запрос будет делаться за времени, а сама структура данных будет занимать памяти.
Содержание
Оптимизация
Для уменьшения количества занимаемой памяти можно провести оптимизацию -мерного дерева отрезков. Для начала, будем использовать дерево отрезков с сохранением всего подотрезка в каждой вершине. Другими словами, в каждой вершине дерева отрезков мы будем хранить не только какую-то сжатую информацию об этом подотрезке, но и все элементы множества , лежащие в этом подотрезке. На первый взгляд, это только увеличит объем структуры, но не все так просто. При построении будем действовать следующим образом — каждый раз дерево отрезков внутри вершины будем строить не по всем элементам множества , а только по сохраненному в этой вершине подотрезку. Действительно, незачем строить дерево по всем элементам, когда элементы вне подотрезка уже были «исключены» и заведомо лежат вне желаемого -мерного прямоугольника. Такое «усеченное» многомерное дерево отрезков называется сжатым (англ. compressed).
Построение дерева
Рассмотрим алгоритм построения сжатого дерева отрезков на примере множества , состоящего из -х взвешенных точек в -мерном пространстве (плоскости):
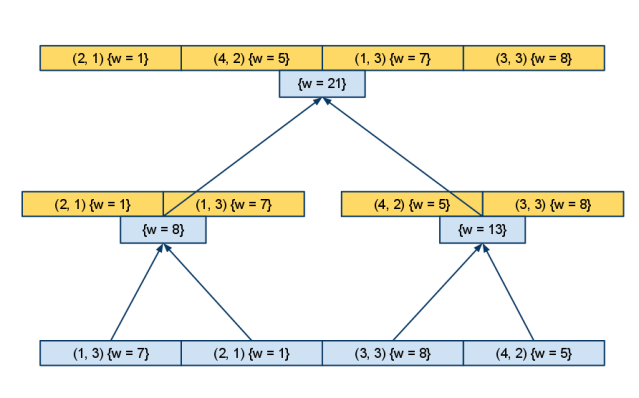
- Cоставим массив из всех элементов множества , упорядочим его по первой координате, построим на нём дерево отрезков с сохранением подмассива в каждой вершине
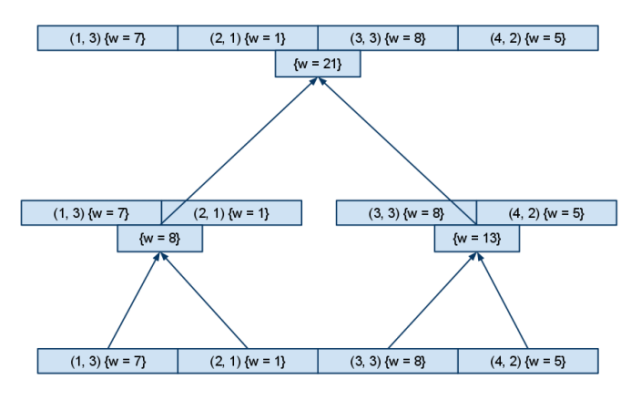
- Повторим построение дерева для каждого из них (координата последняя, поэтому в вершинах этих деревьев мы уже ничего строить не будем — подмассивы в каждой вершине можно не сохранять)
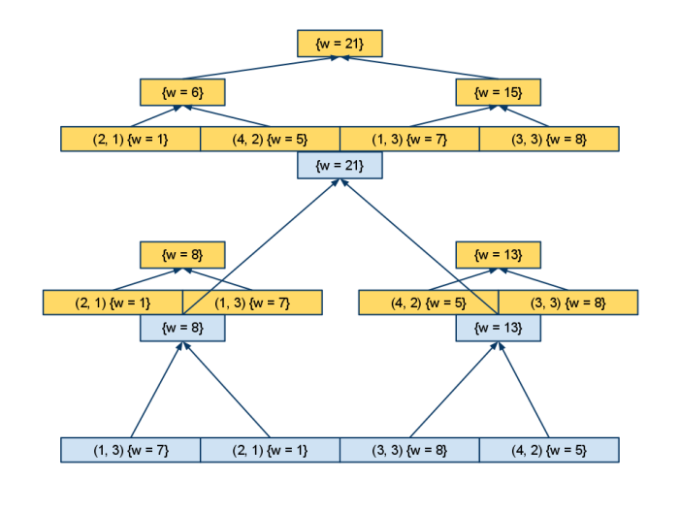
Псевдокод
buildSubarrayTree(element[] array):
// построение одномерного дерева отрезков на массиве array с сохранением подмассива в каждой вершине
buildNormalTree(element[] array):
// построение обычного одномерного дерева отрезков на массиве array
getInsideArray(vertex v):
// получение подмассива, сохраненного в вершине vertex
buildCompressedTree(element[] array, int coordinate = 1): // рекурсивная процедура построения сжатого дерева отрезков
if coordinate < p
sort(array, coordinate) // сортировка массива по нужной координате
segmentTree = buildSubarrayTree(array);
foreach v: vertex in segmentTree
buildCompressedTree(getInsideArray(v), coordinate + 1);
if coordinate == p
sort(array, coordinate)
buildNormalTree(array);
Анализ полученной структуры
Легко понять, что сжатое -мерное дерево отрезков будет занимать памяти: превращение обычного дерева в дерево с сохранением всего подотрезка в каждой вершине будет увеличивать его размер в раз, а сделать это нужно будет раз. Но расплатой станет невозможность делать произвольный запрос модификации: в самом деле, если появится новый элемент, то это приведёт к тому, что мы должны будем в каком-либо дереве отрезков по второй или более координате добавить новый элемент в середину, что эффективно сделать невозможно. Что касается запроса веса, он будет полностью аналогичен запросу в обычном -мерном дереве отрезков за .