Алгоритм Борувки — различия между версиями
(→Реализация) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 25 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | <b>Алгоритм Борувки</b> | + | <b>Алгоритм Борувки</b> (англ. ''Borůvka's algorithm'') {{---}} алгоритм поиска [[Остовные деревья: определения, лемма о безопасном ребре | минимального остовного дерева]] во взвешенном неориентированном связном графе. |
Впервые был опубликован в 1926 году Отакаром Борувкой. | Впервые был опубликован в 1926 году Отакаром Борувкой. | ||
==Описание алгоритма== | ==Описание алгоритма== | ||
| − | |||
| − | + | Алгоритм состоит из нескольких шагов: | |
| − | + | # Изначально каждая вершина графа <tex> G </tex >{{---}} тривиальное дерево, а ребра не принадлежат никакому дереву. | |
| − | # Для | + | # Для каждого дерева <tex> T </tex> найдем минимальное инцидентное ему ребро. Добавим все такие ребра. |
| − | # | + | # Повторяем шаг <tex> 2 </tex> пока в графе не останется только одно дерево <tex> T </tex>. |
| − | |||
| − | Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В <tex>T</tex> могут быть добавлены все три ребра. Избежать эту проблему можно, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером | + | Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В <tex>T</tex> могут быть добавлены все три ребра. Избежать эту проблему можно, например, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером. |
| − | |||
| − | |||
==Доказательство корректности== | ==Доказательство корректности== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{Теорема | ||
| + | |statement= Алгоритм Борувки строит '''MST'''. | ||
| + | |proof=Очевидно, что в результате работы алгоритма получается дерево. Пусть <tex> T </tex> {{---}} минимальное остовное дерево графа <tex> G </tex>, а <tex> T' </tex> {{---}} дерево полученное после работы алгоритма. | ||
| − | + | Покажем, что <tex> T = T'</tex>. | |
| − | |||
| − | |||
| − | |||
| − | + | Предположим обратное <tex> T \neq T' </tex>. Пусть ребро <tex> e' </tex> {{---}} первое добавленное ребро дерева <tex> T' </tex>, не принадлежащее дереву <tex> T </tex>. Пусть <tex> P </tex> {{---}} путь, соединяющий в дереве <tex> T </tex> вершины ребра <tex> e' </tex>. | |
| − | + | Понятно, что в момент, когда ребро <tex> e' </tex> добавляли, какое-то ребро <tex> P </tex> (назовем его <tex> e </tex>) не было добавлено. По алгоритму <tex> w(e) \geqslant w(e') </tex>. Однако тогда <tex> T - e + e' </tex> {{---}} остовное дерево веса не превышающего вес дерева <tex> T </tex>. Получили противоречение. Следовательно <tex> T = T'</tex>. | |
| − | |||
| − | |||
| − | |||
}} | }} | ||
==Реализация== | ==Реализация== | ||
| − | У вершины есть поле comp | + | У вершины есть поле <tex>\mathtt{comp}</tex> {{---}} компонента связности, которой принадлежит эта вершина. |
{| width = 100% | {| width = 100% | ||
|- | |- | ||
| | | | ||
| − | + | <font color=green>// <tex>G</tex> {{---}} исходный граф</font> | |
| − | while T.size < n - 1 // | + | <font color=green>// <tex>w</tex> {{---}} весовая функция</font> |
| − | + | '''function''' <tex>\mathtt{boruvkaMST}():</tex> | |
| − | findComp(T) | + | '''while''' <tex>T\mathtt{.size} < n - 1</tex> |
| − | for | + | '''for''' <tex>k \in </tex> Component <font color = "green">// Component {{---}} множество компонент связности в <tex>T</tex>. Для </font> |
| − | if u.comp | + | <tex>w(\mathtt{minEdge}[k])=\infty</tex> <font color = "green">// каждой компоненты связности вес минимального ребра = <tex>\infty</tex>.</font> |
| − | if minEdge[u.comp] | + | <tex>\mathtt{findComp(}T\mathtt{)}</tex> <font color = "green">// Разбиваем граф <tex>T</tex> на компоненты связности обычным ''dfs''-ом.</font> |
| − | minEdge[u.comp] = | + | '''for''' <tex>\mathtt{(u,v)} \in E </tex> |
| − | if minEdge[v.comp] | + | '''if''' <tex>\mathtt{u.comp} \neq \mathtt{v.comp}</tex> |
| − | minEdge[v.comp] = | + | '''if''' <tex>w(\mathtt{minEdge}[\mathtt{u.comp}]) > w(u,v)</tex> |
| − | for | + | <tex>\mathtt{minEdge}[\mathtt{u.comp}] = (u,v)</tex> |
| − | + | '''if''' <tex>w(\mathtt{minEdge}[\mathtt{v.comp}]) > w(u,v)</tex> | |
| − | return T | + | <tex>\mathtt{minEdge}[\mathtt{v.comp}] = (u,v)</tex> |
| + | '''for''' <tex>k \in </tex> Component | ||
| + | <tex>T\mathtt{.addEdge}(\mathtt{minEdge}[k])</tex> <font color = "green">// Добавляем ребро, если его не было в <tex>T</tex></font> | ||
| + | '''return''' <tex>T</tex> | ||
| + | |} | ||
| + | |||
| + | ==Пример== | ||
| + | {| class = "wikitable" | ||
| + | ! Изображение !! Компоненты связности !! Описание | ||
| + | |-align="center" | ||
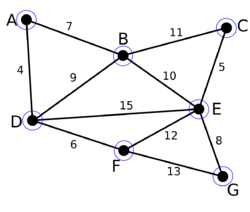
| + | |[[Файл:Boruvka_1.png|250px]] | ||
| + | | <tex>\{A\}</tex><br/><tex>\{B\}</tex><br/><tex>\{C\}</tex><br/><tex>\{D\}</tex><br/><tex>\{E\}</tex><br/><tex>\{F\}</tex><br/><tex>\{G\}</tex> | ||
| + | |Начальный граф <tex>G</tex>. Каждая вершина является компонентой (синие окружности). | ||
| + | |-align="center" | ||
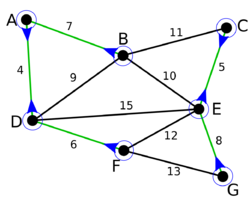
| + | |[[Файл:Boruvka_2.png|250px]] | ||
| + | | <tex>\{ABDF\}</tex><br/><tex>\{CEG\}</tex> | ||
| + | |На первой итерации внешнего цикла для каждой компоненты были добавлены минимальные сопряженные ребра. Некоторые ребра добавлены несколько раз (<tex dpi = 120>AD</tex> и <tex dpi = 120>CE</tex>). Осталось две компоненты. | ||
| + | |-align="center" | ||
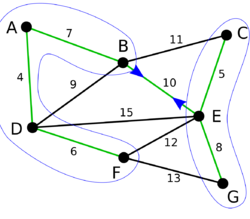
| + | |[[Файл:Boruvka_3.png|250px]] | ||
| + | | <tex>\{ABCDEFG\}</tex> | ||
| + | |На последней итерации внешнего цикла было добавлено минимальное ребро, соединяющее две оставшиеся компоненты (ребро <tex dpi = 120>BE</tex>). Осталась одна компонента. Минимальное остовное дерево графа <tex dpi = 120>G</tex> построено. | ||
| + | |- | ||
|} | |} | ||
==Асимптотика== | ==Асимптотика== | ||
| − | + | На <tex> i </tex>-ой итерации внешнего цикла каждая компонента состоит как минимум из двух компонент из <tex> (i - 1) </tex>-й итерации. Значит, на каждой итерации число компонент уменьшается как минимум в <tex> 2 </tex> раза. Тогда внешний цикл повторяется <tex>O(\log{V})</tex> раз, так как количество компонент изначально равно количеству вершин. Что же касается внутреннего цикла, то он выполняется за <tex>O(E)</tex>, где <tex>E</tex> {{---}} количество рёбер в исходном графе. Следовательно конечное время работы алгоритма <tex>O(E\log{V})</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==См. также== | ==См. также== | ||
* [[Алгоритм Прима]] | * [[Алгоритм Прима]] | ||
* [[Алгоритм Краскала]] | * [[Алгоритм Краскала]] | ||
| + | * [[Алгоритм двух китайцев]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * [http://rain.ifmo.ru/cat/view.php/vis/graph-spanning-trees/mst-2006 Визуализатор алгоритма] | ||
| + | * [http://www.csee.wvu.edu/~ksmani/courses/fa01/random/lecnotes/lecture11.pdf Minimum Spanning Trees] | ||
| + | * [[wikipedia:ru:Алгоритм Борувки|Алгоритм Борувки— Википедия]] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Остовные деревья ]] | [[Категория: Остовные деревья ]] | ||
Текущая версия на 19:07, 4 сентября 2022
Алгоритм Борувки (англ. Borůvka's algorithm) — алгоритм поиска минимального остовного дерева во взвешенном неориентированном связном графе. Впервые был опубликован в 1926 году Отакаром Борувкой.
Содержание
Описание алгоритма
Алгоритм состоит из нескольких шагов:
- Изначально каждая вершина графа — тривиальное дерево, а ребра не принадлежат никакому дереву.
- Для каждого дерева найдем минимальное инцидентное ему ребро. Добавим все такие ребра.
- Повторяем шаг пока в графе не останется только одно дерево .
Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В могут быть добавлены все три ребра. Избежать эту проблему можно, например, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.
Доказательство корректности
| Теорема: |
Алгоритм Борувки строит MST. |
| Доказательство: |
|
Очевидно, что в результате работы алгоритма получается дерево. Пусть — минимальное остовное дерево графа , а — дерево полученное после работы алгоритма. Покажем, что . Предположим обратное . Пусть ребро — первое добавленное ребро дерева , не принадлежащее дереву . Пусть — путь, соединяющий в дереве вершины ребра . Понятно, что в момент, когда ребро добавляли, какое-то ребро (назовем его ) не было добавлено. По алгоритму . Однако тогда — остовное дерево веса не превышающего вес дерева . Получили противоречение. Следовательно . |
Реализация
У вершины есть поле — компонента связности, которой принадлежит эта вершина.
// — исходный граф // — весовая функция function while for Component // Component — множество компонент связности в . Для // каждой компоненты связности вес минимального ребра = . // Разбиваем граф на компоненты связности обычным dfs-ом. for if if if for Component // Добавляем ребро, если его не было в return |
Пример
Асимптотика
На -ой итерации внешнего цикла каждая компонента состоит как минимум из двух компонент из -й итерации. Значит, на каждой итерации число компонент уменьшается как минимум в раза. Тогда внешний цикл повторяется раз, так как количество компонент изначально равно количеству вершин. Что же касается внутреннего цикла, то он выполняется за , где — количество рёбер в исходном графе. Следовательно конечное время работы алгоритма .