|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | <b>Алгоритм Борувки</b> (англ. ''Borůvka's algorithm'') {{---}} алгоритм поиска [[Остовные деревья: определения, лемма о безопасном ребре | минимального остовного дерева]] во взвешенном неориентированном связном графе. | | <b>Алгоритм Борувки</b> (англ. ''Borůvka's algorithm'') {{---}} алгоритм поиска [[Остовные деревья: определения, лемма о безопасном ребре | минимального остовного дерева]] во взвешенном неориентированном связном графе. |
| | Впервые был опубликован в 1926 году Отакаром Борувкой. | | Впервые был опубликован в 1926 году Отакаром Борувкой. |
Текущая версия на 19:07, 4 сентября 2022
Алгоритм Борувки (англ. Borůvka's algorithm) — алгоритм поиска минимального остовного дерева во взвешенном неориентированном связном графе.
Впервые был опубликован в 1926 году Отакаром Борувкой.
Описание алгоритма
Алгоритм состоит из нескольких шагов:
- Изначально каждая вершина графа [math] G [/math]— тривиальное дерево, а ребра не принадлежат никакому дереву.
- Для каждого дерева [math] T [/math] найдем минимальное инцидентное ему ребро. Добавим все такие ребра.
- Повторяем шаг [math] 2 [/math] пока в графе не останется только одно дерево [math] T [/math].
Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В [math]T[/math] могут быть добавлены все три ребра. Избежать эту проблему можно, например, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.
Доказательство корректности
| Теорема: |
Алгоритм Борувки строит MST. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Очевидно, что в результате работы алгоритма получается дерево. Пусть [math] T [/math] — минимальное остовное дерево графа [math] G [/math], а [math] T' [/math] — дерево полученное после работы алгоритма.
Покажем, что [math] T = T'[/math].
Предположим обратное [math] T \neq T' [/math]. Пусть ребро [math] e' [/math] — первое добавленное ребро дерева [math] T' [/math], не принадлежащее дереву [math] T [/math]. Пусть [math] P [/math] — путь, соединяющий в дереве [math] T [/math] вершины ребра [math] e' [/math].
Понятно, что в момент, когда ребро [math] e' [/math] добавляли, какое-то ребро [math] P [/math] (назовем его [math] e [/math]) не было добавлено. По алгоритму [math] w(e) \geqslant w(e') [/math]. Однако тогда [math] T - e + e' [/math] — остовное дерево веса не превышающего вес дерева [math] T [/math]. Получили противоречение. Следовательно [math] T = T'[/math]. |
| [math]\triangleleft[/math] |
Реализация
У вершины есть поле [math]\mathtt{comp}[/math] — компонента связности, которой принадлежит эта вершина.
// [math]G[/math] — исходный граф
// [math]w[/math] — весовая функция
function [math]\mathtt{boruvkaMST}():[/math]
while [math]T\mathtt{.size} \lt n - 1[/math]
for [math]k \in [/math] Component // Component — множество компонент связности в [math]T[/math]. Для
[math]w(\mathtt{minEdge}[k])=\infty[/math] // каждой компоненты связности вес минимального ребра = [math]\infty[/math].
[math]\mathtt{findComp(}T\mathtt{)}[/math] // Разбиваем граф [math]T[/math] на компоненты связности обычным dfs-ом.
for [math]\mathtt{(u,v)} \in E [/math]
if [math]\mathtt{u.comp} \neq \mathtt{v.comp}[/math]
if [math]w(\mathtt{minEdge}[\mathtt{u.comp}]) \gt w(u,v)[/math]
[math]\mathtt{minEdge}[\mathtt{u.comp}] = (u,v)[/math]
if [math]w(\mathtt{minEdge}[\mathtt{v.comp}]) \gt w(u,v)[/math]
[math]\mathtt{minEdge}[\mathtt{v.comp}] = (u,v)[/math]
for [math]k \in [/math] Component
[math]T\mathtt{.addEdge}(\mathtt{minEdge}[k])[/math] // Добавляем ребро, если его не было в [math]T[/math]
return [math]T[/math]
|
Пример
| Изображение |
Компоненты связности |
Описание
|
|
[math]\{A\}[/math]
[math]\{B\}[/math]
[math]\{C\}[/math]
[math]\{D\}[/math]
[math]\{E\}[/math]
[math]\{F\}[/math]
[math]\{G\}[/math]
|
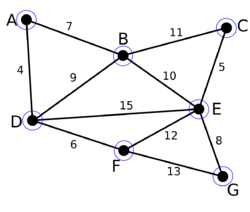
Начальный граф [math]G[/math]. Каждая вершина является компонентой (синие окружности).
|
|
[math]\{ABDF\}[/math]
[math]\{CEG\}[/math]
|
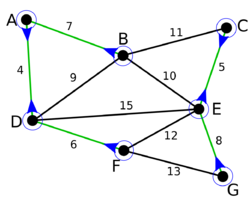
На первой итерации внешнего цикла для каждой компоненты были добавлены минимальные сопряженные ребра. Некоторые ребра добавлены несколько раз ([math]AD[/math] и [math]CE[/math]). Осталось две компоненты.
|
|
[math]\{ABCDEFG\}[/math]
|
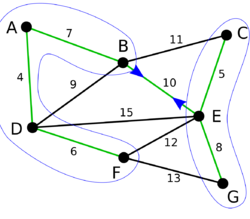
На последней итерации внешнего цикла было добавлено минимальное ребро, соединяющее две оставшиеся компоненты (ребро [math]BE[/math]). Осталась одна компонента. Минимальное остовное дерево графа [math]G[/math] построено.
|
Асимптотика
На [math] i [/math]-ой итерации внешнего цикла каждая компонента состоит как минимум из двух компонент из [math] (i - 1) [/math]-й итерации. Значит, на каждой итерации число компонент уменьшается как минимум в [math] 2 [/math] раза. Тогда внешний цикл повторяется [math]O(\log{V})[/math] раз, так как количество компонент изначально равно количеству вершин. Что же касается внутреннего цикла, то он выполняется за [math]O(E)[/math], где [math]E[/math] — количество рёбер в исходном графе. Следовательно конечное время работы алгоритма [math]O(E\log{V})[/math].
См. также
Источники информации


