Схема Бернулли — различия между версиями
Sergej (обсуждение | вклад) (→Пример) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 143 промежуточные версии 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''' | + | {{Определение |
| − | + | |definition= | |
| + | '''Схемой Бернулли''' (англ. ''Bernoulli scheme'') называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода {{---}} «успех» и «неудача», при этом успех в каждом испытании происходит с одной и той же вероятностью <tex> p \in (0, 1)</tex> , а неудача {{---}} с вероятностью <tex> q = 1 - p </tex>. | ||
| + | }} | ||
| + | == Распределение Бернулли== | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | + | '''Распределение Бернулли''' (англ. ''Bernoulli distribution'') {{---}} описывает ситуации, где "испытание" имеет результат "успех" либо "неуспех". | |
}} | }} | ||
| − | + | [[Дискретная случайная величина | Случайная величина]] <tex>\xi</tex> с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью <tex>p</tex> успеха : ни одного успеха или один успех. Функция распределения <tex> \xi</tex> имеет вид | |
| + | |||
| + | <tex> | ||
| + | F_{\xi}(x) = P(\xi < x) \begin{cases} | ||
| + | 0, & x\leqslant 0 \\ | ||
| + | 1 - p, & 0 < x \leqslant 1\\ | ||
| + | 1, & x > 1 | ||
| + | \end{cases} | ||
| + | </tex> | ||
| − | + | [[Файл:Распределение Бернулли.jpg]] | |
| − | + | ||
| − | + | == Биномиальное распределение == | |
| − | + | {{Определение | |
| − | + | |definition= | |
| − | | | + | Случайная величина <tex>\xi</tex> имеет '''биномиальное распределение''' (англ. ''binomial distribution'') с параметрами <tex>n \in \mathbb N</tex> и <tex> p \in (0, 1)</tex> и пишут: <tex> \xi \in \mathbb B_{n, p}</tex> если <tex> \xi</tex> принимает значения <tex>k = 0, 1, \ldots ,n</tex> с вероятностями <tex >P(\xi = k) = </tex><tex > \dbinom{n}{k} \cdot p^k \cdot (1 - p)^{n - k} </tex> . |
| − | |||
}} | }} | ||
| + | Случайная величина с таким распределением имеет смысл числа успехов в <tex> n </tex> испытаниях схемы Бернулли с вероятностью успеха <tex>p</tex>. | ||
| − | + | Таблица распределения <tex> \xi </tex> имеет вид | |
| − | |||
| − | + | {| class="wikitable" style ="text-align:center" | |
| + | |- | ||
| + | |<tex>\xi </tex> | ||
| + | | 0 | ||
| + | | 1 | ||
| + | | <tex>\ldots</tex> | ||
| + | | <tex>k</tex> | ||
| + | | <tex>\ldots</tex> | ||
| + | | <tex>n</tex> | ||
| + | |- | ||
| + | | <tex>P</tex> | ||
| + | | <tex>(1 - p) ^ n </tex> | ||
| + | | <tex>n \cdot p \cdot (1 - p)^{n - 1}</tex> | ||
| + | | <tex>\ldots</tex> | ||
| + | | <tex>\dbinom{n}{k} \cdot p^k \cdot (1 - p)^{n - k} </tex> | ||
| + | | <tex>\ldots</tex> | ||
| + | | <tex> p^n </tex> | ||
| + | |} | ||
| − | <tex> | + | == Формула Бернулли == |
| + | Обозначим через <tex> v_{n} </tex> число успехов, случившихся в <tex> n</tex> испытаниях схемы Бернулли. Эта случайная величина может принимать целые значения от <tex>0</tex> до <tex>n</tex> в зависимости от результатов испытаний. Например, если все <tex>n </tex> испытаний завершились неудачей, то величина <tex> v_{n} </tex> равна нулю. | ||
| − | <tex>P(v_{ | + | {{Теорема |
| + | |id=th1 | ||
| + | |statement= | ||
| + | Для любого <tex >k = 0, 1, \ldots , n </tex> вероятность получить в <tex>n</tex> испытаниях <tex>k</tex> успехов равна <tex> P(v_{n} = k ) = </tex> <tex dpi="145"> \dbinom{n}{k} \cdot p^{k} \cdot q^{n - k}</tex> | ||
| − | <tex> | + | |proof= |
| + | Событие <tex>\{A = v_{n} = k\}</tex> означает, что в <tex>n</tex> испытаниях схемы Бернулли произошло ровно <tex>k</tex> успехов. Рассмотрим один элементарный исход из события <tex>A</tex>: когда первые <tex>k</tex> испытаний завершились успехом, остальные неудачей. Поскольку испытания независимы, вероятность такого элементарного исхода равна <tex> p ^ {k} \cdot (1-p) ^ {n - k} </tex> Другие элементарные исходы из события <tex>A</tex> отличаются лишь расположением <tex>k</tex> успехов на <tex>n</tex> местах. Есть ровно <tex dpi="145">\dbinom{n}{k}</tex> способов расположить <tex>k</tex> успехов на <tex>n</tex> местах. Поэтому событие <tex>A</tex> состоит из <tex dpi="145">\dbinom{n}{k}</tex> элементарных исходов, вероятность каждого из которых равна <tex> p ^ {k} \cdot q ^ {n - k}</tex> | ||
| + | Набор вероятностей в теореме называется биномиальным распределением вероятностей. | ||
| + | }} | ||
| − | + | == Геометрическое распределение == | |
| − | + | {{Определение | |
| + | |definition= | ||
| + | '''Геометрическое распределение''' (англ. ''geometric distribution'') {{---}} распределение дискретной случайной величины, равной количеству испытаний случайного эксперимента до наблюдения первого успеха. | ||
| + | }} | ||
| − | |||
{{Лемма | {{Лемма | ||
|id=th1 | |id=th1 | ||
|statement= | |statement= | ||
| − | Вероятность того, что первый успех произойдёт в испытании с номером <tex>k \in \mathbb N = {1, 2, 3, | + | Вероятность того, что первый успех произойдёт в испытании с номером <tex>k \in \mathbb N = {1, 2, 3, \ldots}</tex> равна <tex>P(r = k) = p \cdot q^ {k - 1} </tex> |
| − | |||
|proof= | |proof= | ||
| − | Вероятность первым <tex> k </tex> | + | Вероятность первым <tex> k - 1 </tex> испытаниям завершиться неудачей, а последнему {{---}} успехом, равна <tex> P(r = k) = p \cdot q^{k - 1} </tex> |
}} | }} | ||
| Строка 45: | Строка 80: | ||
|id=th1 | |id=th1 | ||
|statement= | |statement= | ||
| − | Пусть <tex> P(r = k) = | + | Пусть <tex> P(r = k) = p \cdot q^{k - 1} </tex> для любого <tex> k \in \mathbb N </tex>. Тогда для любых неотрицательных целых <tex>n </tex> и <tex>k</tex> имеет место равенство: <tex> P(r > n + k | r > n) = P(r > k) </tex> |
|proof= | |proof= | ||
По определению условной вероятности, | По определению условной вероятности, | ||
| − | <tex> P(r > n + k | r > n) = \ | + | <tex > P(r > n + k | r > n) = </tex> <tex> \dfrac{P(r > n + k, r > n)}{P(r > n)} = \dfrac{P(r > n + k)}{P(r > n)} </tex> <tex>\left(1\right)</tex> |
| − | Последнее равенство верно в силу того, что событие <tex> {r > n + k} </tex> влечёт событие <tex>{r > n}</tex>, поэтому их пересечением будет событие <tex> {r > n + k}</tex>. Найдём для целого <tex> m \ | + | Последнее равенство верно в силу того, что событие <tex> {r > n + k} </tex> влечёт событие <tex>{r > n}</tex>, поэтому их пересечением будет событие <tex> {r > n + k}</tex>. Найдём для целого <tex> m \geqslant 0</tex> вероятность <tex> P(r > m)</tex> : событие <tex> r > m </tex> означает,что в схеме Бернулли первые <tex>m</tex> испытаний завершились «неудачами», то есть его вероятность равна <tex> q^{m}</tex>. Возвращаясь к формуле <tex>\left(1\right)</tex> получаем, что эта [[Дискретная случайная величина | случайная величина]] равна <tex > P(r > n + k | r > n) = </tex> <tex> \dfrac{P(r > n + k, r > n)}{P(r > n)} = \dfrac{q^{n + k}} {q^{n}} =</tex> <tex> q^{k} = P(r > k)</tex>. |
| + | |||
}} | }} | ||
| − | == | + | == Обобщение (полиномиальная схема) == |
| + | Обычная формула Бернулли применима на случай, когда при каждом испытании возможен один из двух исходов. | ||
| + | Рассмотрим случай, когда в одном испытании возможны <tex> m</tex> исходов: <tex>1, 2, \ldots , m,</tex> и <tex>i</tex>-й исход в одном испытании случается | ||
| + | с вероятностью <tex> p_{i}</tex> , где <tex>p_{1} + \ldots + p_{m} = 1</tex>. | ||
| + | {{Теорема | ||
| + | |id=th1 | ||
| + | |statement= | ||
| + | Обозначим через <tex>P(n_{1}, \ldots , n_{m})</tex> вероятность того, что в <tex>n</tex> независимых испытаниях первый исход случится <tex> n_{1}</tex> раз, второй исход {{---}} <tex>n_{2}</tex> раз, и так далее, наконец, <tex>m</tex>-й исход {{---}} <tex>n_{m}</tex> раз тогда верна формула: | ||
| + | <tex > P(n_{1}, \ldots , n_{m}) = </tex> <tex> \dfrac{n!}{n_{1}! \cdot n_{2}! \cdot\ldots \cdot n_{m}!} \cdot {p_{1}}^{n_{1}} \cdot \ldots \cdot {p_{m}}^{n_{m}} | ||
| + | </tex> | ||
| + | |proof= | ||
| + | Рассмотрим один элементарный исход, благоприятствующий выпадению <tex>n_{1}</tex> единиц, <tex> n_{2}</tex> двоек, и так далее. | ||
| + | Это результат <tex>n</tex> экспериментов, когда все нужные исходы появились в некотором заранее заданном порядке. Вероятность такого результата равна произведению вероятностей <tex>p_{n_{1}} \ldots p_{n_{m}}</tex>. Остальные благоприятные исходы отличаются лишь расположением чисел <tex>1, 2, \ldots , m</tex> на <tex>n</tex> местах. Число таких исходов равно числу способов расположить на <tex>n</tex> местах <tex>n_{1}</tex> единиц, <tex>n_{2}</tex> двоек,и так далее Это число равно | ||
| + | <tex>\dbinom{n}{n_1} \cdot\dbinom{n - n_1 - n_2}{n_2} \cdot \dbinom{n - n_1 - n_2- n_3}{n_3} \cdot\ldots \cdot \dbinom{n - n_1 - n_2 - \ldots - n_{m -1}}{n_m} = \dfrac {n!}{n_{1}! \cdot n_{2}! \cdot \ldots \cdot n_{m}!} | ||
| + | </tex> | ||
| + | }} | ||
| + | |||
| + | == Примеры == | ||
| + | ==== Правильная монета ==== | ||
| + | Правильная монета подбрасывается <tex>10</tex> раз. Найти вероятность того, что герб выпадет от <tex>4</tex> до <tex>6</tex> раз. | ||
| + | |||
| + | Вычислим отдельно вероятности получить <tex>4, 5</tex> и <tex>6</tex> гербов после десяти подбрасываний монеты. | ||
| + | |||
| + | <tex >P(v_{10} = 4) =</tex> <tex> \dbinom{10}{4} \cdot\left(\dfrac{1}{2}\right)^ {4} \cdot \left(\dfrac{1}{2}\right)^ {10 - 4} </tex> <tex>~\approx ~ 0{.}205 </tex> | ||
| + | |||
| + | <tex >P(v_{10} = 5) = </tex> <tex>\dbinom{10}{5} \cdot \left(\dfrac{1}{2}\right)^ {5} \cdot \left(\dfrac{1}{2}\right)^ {10 - 5}</tex><tex>~\approx ~ 0{.}246 </tex> | ||
| + | |||
| + | <tex >P(v_{10} = 6) =</tex> <tex> \dbinom{10}{6} \cdot \left(\dfrac{1}{2}\right)^ {6} \cdot \left(\dfrac{1}{2}\right)^ {10 - 6}</tex> <tex>~\approx ~ 0{.}205 </tex> | ||
| + | |||
| + | Сложим вероятности несовместных событий: | ||
| + | <tex>P(4 \leqslant v_{10} \leqslant 6) = P(v_{10} = 4) + P(v_{10} = 5) + P(v_{10} = 6) ~\approx ~ 0{.}656 </tex> | ||
| + | |||
| + | ==== Правильная игральная кость с двумя исходами ==== | ||
Два игрока по очереди подбрасывают правильную игральную кость. Выигрывает тот, кто первым выкинет шесть очков. Найти вероятность победы игрока, начинающего игру. | Два игрока по очереди подбрасывают правильную игральную кость. Выигрывает тот, кто первым выкинет шесть очков. Найти вероятность победы игрока, начинающего игру. | ||
| − | Шесть очков может впервые выпасть при первом, втором, и так далее. бросках кости. Первый игрок побеждает, если это случится при броске с нечётным номером, второй | + | Шесть очков может впервые выпасть при первом, втором, и так далее. бросках кости. Первый игрок побеждает, если это случится при броске с нечётным номером, второй {{---}} с чётным. Пусть событие <tex> A_{k} </tex> состоит в том, что шесть очков впервые выпадет в испытании с номером <tex>k</tex>. По лемме, <tex > P(A_{k}) =</tex> <tex>\dfrac{1}{6} \cdot \left(\dfrac{5}{6}\right)^{k - 1} </tex> |
| − | События <tex>A , B</tex>, означающие победу первого и второго игроков соответственно, представимы в виде объединения | + | События <tex>A , B</tex>, означающие победу первого и второго игроков соответственно, представимы в виде объединения взаимоисключающих событий: |
| − | <tex> A = A_{1} \cup A_{3} \cup A_{5} \cup | + | <tex> A = A_{1} \cup A_{3} \cup A_{5} \cup \ldots , B = B_{2}\cup B_{4} \cup B_{6} \cup \ldots </tex> |
Вероятности этих объединений равны суммам вероятностей слагаемых: | Вероятности этих объединений равны суммам вероятностей слагаемых: | ||
| − | <tex> P(A) = \ | + | <tex > P(A) =</tex><tex> \dfrac{1}{6} + \dfrac{1}{6} \cdot \left(\dfrac{5}{6}\right)^{2} + \dfrac{1}{6} \cdot\left(\dfrac{5}{6}\right)^{4} \ldots = \dfrac{6}{11}.</tex> Теперь аналогичным образом посчитаю вероятность для события <tex>B</tex> |
| − | <tex> | + | <tex> P(B) =</tex> <tex> \dfrac{1}{6} \cdot \dfrac{5}{6} + \dfrac{1}{6} \cdot \left(\dfrac{5}{6}\right)^{3} + \dfrac{1}{6} \cdot\left(\dfrac{5}{6}\right)^{5} \ldots = \dfrac{5}{11}. |
| − | P(B) = \ | ||
</tex> | </tex> | ||
| − | + | ==== Правильная игральная кость с тремя исходами ==== | |
| − | |||
| − | == | ||
Игральная кость подбрасывается пятнадцать раз. Найти вероятность того, что выпадет ровно десять троек и три единицы. | Игральная кость подбрасывается пятнадцать раз. Найти вероятность того, что выпадет ровно десять троек и три единицы. | ||
| − | Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани. | + | Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Так как вероятности выпадения тройки и единицы равны по <tex>\dfrac{1}{6}</tex>, а вероятность третьего исхода (выпала любая другая грань) <tex>\dfrac{4}{6}</tex>, то вероятность получить десять троек, три единицы и ещё два других очка равна | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <tex> P(10, 3, 2) = \ | + | <tex > P(10, 3, 2) = </tex> <tex> \dfrac{15!}{10! \cdot 3! \cdot2!} \cdot \left(\dfrac{1}{6}\right)^{10} \cdot \left(\dfrac{1}{6}\right)^{3} \cdot \left(\dfrac{4}{6}\right)^{2} |
</tex> | </tex> | ||
==См. также== | ==См. также== | ||
| − | |||
*[[Дискретная случайная величина]] | *[[Дискретная случайная величина]] | ||
*[[Математическое ожидание случайной величины]] | *[[Математическое ожидание случайной величины]] | ||
| − | == | + | ==Источники информации== |
| − | *Н.И Чернова 'Теория вероятности | + | *[https://ru.wikipedia.org/wiki/Распределение_Бернулли Википедия {{---}} Распределение Бернулли] |
| + | *[https://ru.wikipedia.org/wiki/Биномиальное_распределение Википедия {{---}} Биномиальное распределение] | ||
| + | *[https://ru.wikipedia.org/wiki/Формула_Бернулли Википедия {{---}} Формула Бернулли] | ||
| + | *[https://ru.wikipedia.org/wiki/Геометрическое_распределение Википедия {{---}} Геометрическое распределение] | ||
| + | *''Н.И Чернова'' Теория вероятности {{---}} Новосибирск, 2009. | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Теория вероятности]] | [[Категория: Теория вероятности]] | ||
Текущая версия на 19:07, 4 сентября 2022
| Определение: |
| Схемой Бернулли (англ. Bernoulli scheme) называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача», при этом успех в каждом испытании происходит с одной и той же вероятностью , а неудача — с вероятностью . |
Содержание
Распределение Бернулли
| Определение: |
| Распределение Бернулли (англ. Bernoulli distribution) — описывает ситуации, где "испытание" имеет результат "успех" либо "неуспех". |
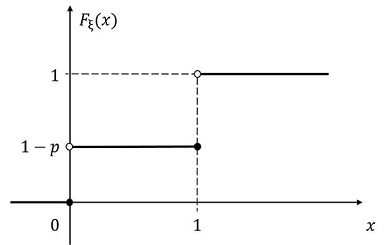
Случайная величина с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха : ни одного успеха или один успех. Функция распределения имеет вид
Биномиальное распределение
| Определение: |
| Случайная величина имеет биномиальное распределение (англ. binomial distribution) с параметрами и и пишут: если принимает значения с вероятностями . |
Случайная величина с таким распределением имеет смысл числа успехов в испытаниях схемы Бернулли с вероятностью успеха .
Таблица распределения имеет вид
| 0 | 1 | |||||
Формула Бернулли
Обозначим через число успехов, случившихся в испытаниях схемы Бернулли. Эта случайная величина может принимать целые значения от до в зависимости от результатов испытаний. Например, если все испытаний завершились неудачей, то величина равна нулю.
| Теорема: |
Для любого вероятность получить в испытаниях успехов равна |
| Доказательство: |
|
Событие означает, что в испытаниях схемы Бернулли произошло ровно успехов. Рассмотрим один элементарный исход из события : когда первые испытаний завершились успехом, остальные неудачей. Поскольку испытания независимы, вероятность такого элементарного исхода равна Другие элементарные исходы из события отличаются лишь расположением успехов на местах. Есть ровно способов расположить успехов на местах. Поэтому событие состоит из элементарных исходов, вероятность каждого из которых равна Набор вероятностей в теореме называется биномиальным распределением вероятностей. |
Геометрическое распределение
| Определение: |
| Геометрическое распределение (англ. geometric distribution) — распределение дискретной случайной величины, равной количеству испытаний случайного эксперимента до наблюдения первого успеха. |
| Лемма: |
Вероятность того, что первый успех произойдёт в испытании с номером равна |
| Доказательство: |
| Вероятность первым испытаниям завершиться неудачей, а последнему — успехом, равна |
| Теорема: |
Пусть для любого . Тогда для любых неотрицательных целых и имеет место равенство: |
| Доказательство: |
|
По определению условной вероятности, Последнее равенство верно в силу того, что событие влечёт событие , поэтому их пересечением будет событие . Найдём для целого вероятность : событие означает,что в схеме Бернулли первые испытаний завершились «неудачами», то есть его вероятность равна . Возвращаясь к формуле получаем, что эта случайная величина равна . |
Обобщение (полиномиальная схема)
Обычная формула Бернулли применима на случай, когда при каждом испытании возможен один из двух исходов. Рассмотрим случай, когда в одном испытании возможны исходов: и -й исход в одном испытании случается с вероятностью , где .
| Теорема: |
Обозначим через вероятность того, что в независимых испытаниях первый исход случится раз, второй исход — раз, и так далее, наконец, -й исход — раз тогда верна формула:
|
| Доказательство: |
|
Рассмотрим один элементарный исход, благоприятствующий выпадению единиц, двоек, и так далее. Это результат экспериментов, когда все нужные исходы появились в некотором заранее заданном порядке. Вероятность такого результата равна произведению вероятностей . Остальные благоприятные исходы отличаются лишь расположением чисел на местах. Число таких исходов равно числу способов расположить на местах единиц, двоек,и так далее Это число равно |
Примеры
Правильная монета
Правильная монета подбрасывается раз. Найти вероятность того, что герб выпадет от до раз.
Вычислим отдельно вероятности получить и гербов после десяти подбрасываний монеты.
Сложим вероятности несовместных событий:
Правильная игральная кость с двумя исходами
Два игрока по очереди подбрасывают правильную игральную кость. Выигрывает тот, кто первым выкинет шесть очков. Найти вероятность победы игрока, начинающего игру.
Шесть очков может впервые выпасть при первом, втором, и так далее. бросках кости. Первый игрок побеждает, если это случится при броске с нечётным номером, второй — с чётным. Пусть событие состоит в том, что шесть очков впервые выпадет в испытании с номером . По лемме, События , означающие победу первого и второго игроков соответственно, представимы в виде объединения взаимоисключающих событий: Вероятности этих объединений равны суммам вероятностей слагаемых:
Теперь аналогичным образом посчитаю вероятность для события
Правильная игральная кость с тремя исходами
Игральная кость подбрасывается пятнадцать раз. Найти вероятность того, что выпадет ровно десять троек и три единицы. Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани.
Так как вероятности выпадения тройки и единицы равны по , а вероятность третьего исхода (выпала любая другая грань) , то вероятность получить десять троек, три единицы и ещё два других очка равна
См. также
Источники информации
- Википедия — Распределение Бернулли
- Википедия — Биномиальное распределение
- Википедия — Формула Бернулли
- Википедия — Геометрическое распределение
- Н.И Чернова Теория вероятности — Новосибирск, 2009.