Расширенные биномиальные коэффициенты — различия между версиями
(I am dark black переименовал страницу Расширенные биномиальные коэффициенты в А что звучит хайпово) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 2 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{в разработке}} | |
| + | |||
| + | {{Определение | ||
| + | |definition= В математике '''биномиальные коэффициенты''' {{---}} коэффициенты в разложении бинома Ньютона <tex>(1+x)^n</tex> по степеням <tex>x</tex>.}} | ||
| + | |||
| + | Коэффициенты при <tex>x^k</tex> обозначаются <tex>\binom{n}{k}</tex> и вычисляются по формуле | ||
| + | |||
| + | <tex>\dbinom{n}{k} = \dfrac{n!}{k!(n-k)!}</tex>. | ||
| + | |||
| + | Значение выражения определено при целых неотрицательных <tex>n</tex> и <tex>k</tex>. Однако видно, что дробь можно сократить на <tex>(n-k)!</tex>. | ||
| + | |||
| + | <tex>\dbinom{n}{k} = \dfrac{n(n-1)\ldots(n-k+1)}{k!}</tex>. | ||
| + | |||
| + | В этом выражении <tex>n</tex> может принимать произвольные действительные значения. | ||
| + | |||
| + | ==Расширение треугольника Паскаля== | ||
| + | [[Файл:Pascalstriangle.PNG|300px|thumb|right|Расширенный треугольник Паскаля]] | ||
| + | |||
| + | Нетрудно проверить, что для биномиальных коэффициентов справедливо равенство: | ||
| + | |||
| + | <tex>\dbinom{n}{k} = \dbinom{n-1}{k-1} + \dbinom{n-1}{k} </tex>. | ||
| + | |||
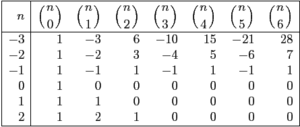
| + | При этом <tex>\binom{n}{0} = 1</tex>. Это свойство позволяет продлить треугольник Паскаля в сторону отрицательных значений <tex>n</tex>, причём единственным образом. | ||
| + | |||
| + | |||
| + | ==Применение== | ||
| + | Расширенный треугольник Паскаля позволяет раскладывать в ряд простые дроби. | ||
| + | |||
| + | Например, <tex>\dfrac{1}{(1+z)^2} = (1+z)^{-2} = \displaystyle\sum\limits_{k=0}^\infty\dbinom{-2}{k}z^k</tex>. | ||
| + | |||
| + | В общем случае <tex>\dfrac{1}{(1+z)^n} = (1+z)^{-n} = \displaystyle\sum\limits_{k=0}^\infty\dbinom{-n}{k}z^k</tex>. | ||
| + | |||
| + | == См. также == | ||
| + | |||
| + | * [[Производящая функция]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * [http://www.genfunc.ru/theory/pril02/ Расширенные биномиальные коэффициенты] | ||
| + | * [https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BA%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82 Биномиальный коэффициент {{---}} Википедия] | ||
| + | * [http://kvant.mirror1.mccme.ru/1988/11/razbienie_chisel.htm Вайнштейн Ф., Разбиение чисел. Журнал "Квант" № 11, 1988 год] | ||
| + | * [http://www.genfunc.ru/ Производящие функции] | ||
| + | * [http://en.wikipedia.org/wiki/Generating_function Wikipedia {{---}} Generating function] | ||
| + | * [[Нахождение количества разбиений числа на слагаемые|Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера]] | ||
| + | * Graham, Knuth, and Patashnik: Concrete Mathematics | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Комбинаторика]] | ||
| + | [[Категория: Подсчёт числа объектов]] | ||
Текущая версия на 19:08, 4 сентября 2022
Эта статья находится в разработке!
| Определение: |
| В математике биномиальные коэффициенты — коэффициенты в разложении бинома Ньютона по степеням . |
Коэффициенты при обозначаются и вычисляются по формуле
.
Значение выражения определено при целых неотрицательных и . Однако видно, что дробь можно сократить на .
.
В этом выражении может принимать произвольные действительные значения.
Расширение треугольника Паскаля
Нетрудно проверить, что для биномиальных коэффициентов справедливо равенство:
.
При этом . Это свойство позволяет продлить треугольник Паскаля в сторону отрицательных значений , причём единственным образом.
Применение
Расширенный треугольник Паскаля позволяет раскладывать в ряд простые дроби.
Например, .
В общем случае .
См. также
Источники информации
- Расширенные биномиальные коэффициенты
- Биномиальный коэффициент — Википедия
- Вайнштейн Ф., Разбиение чисел. Журнал "Квант" № 11, 1988 год
- Производящие функции
- Wikipedia — Generating function
- Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера
- Graham, Knuth, and Patashnik: Concrete Mathematics