Расширенные биномиальные коэффициенты — различия между версиями
Nsychev (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
| (не показана 1 промежуточная версия 1 участника) | |
(нет различий)
| |
Текущая версия на 19:08, 4 сентября 2022
Эта статья находится в разработке!
| Определение: |
| В математике биномиальные коэффициенты — коэффициенты в разложении бинома Ньютона по степеням . |
Коэффициенты при обозначаются и вычисляются по формуле
.
Значение выражения определено при целых неотрицательных и . Однако видно, что дробь можно сократить на .
.
В этом выражении может принимать произвольные действительные значения.
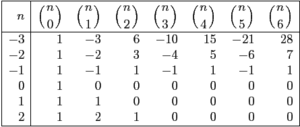
Расширение треугольника Паскаля
Нетрудно проверить, что для биномиальных коэффициентов справедливо равенство:
.
При этом . Это свойство позволяет продлить треугольник Паскаля в сторону отрицательных значений , причём единственным образом.
Применение
Расширенный треугольник Паскаля позволяет раскладывать в ряд простые дроби.
Например, .
В общем случае .
См. также
Источники информации
- Расширенные биномиальные коэффициенты
- Биномиальный коэффициент — Википедия
- Вайнштейн Ф., Разбиение чисел. Журнал "Квант" № 11, 1988 год
- Производящие функции
- Wikipedia — Generating function
- Нахождение количества разбиений числа на слагаемые. Пентагональная теорема Эйлера
- Graham, Knuth, and Patashnik: Concrete Mathematics