|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | {{в разработке}} | | {{в разработке}} |
| | | | |
Текущая версия на 19:08, 4 сентября 2022
Эта статья находится в разработке!
| Определение: |
| В математике биномиальные коэффициенты — коэффициенты в разложении бинома Ньютона [math](1+x)^n[/math] по степеням [math]x[/math]. |
Коэффициенты при [math]x^k[/math] обозначаются [math]\binom{n}{k}[/math] и вычисляются по формуле
[math]\dbinom{n}{k} = \dfrac{n!}{k!(n-k)!}[/math].
Значение выражения определено при целых неотрицательных [math]n[/math] и [math]k[/math]. Однако видно, что дробь можно сократить на [math](n-k)![/math].
[math]\dbinom{n}{k} = \dfrac{n(n-1)\ldots(n-k+1)}{k!}[/math].
В этом выражении [math]n[/math] может принимать произвольные действительные значения.
Расширение треугольника Паскаля
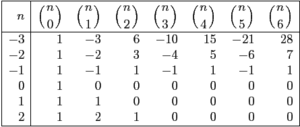
Расширенный треугольник Паскаля
Нетрудно проверить, что для биномиальных коэффициентов справедливо равенство:
[math]\dbinom{n}{k} = \dbinom{n-1}{k-1} + \dbinom{n-1}{k} [/math].
При этом [math]\binom{n}{0} = 1[/math]. Это свойство позволяет продлить треугольник Паскаля в сторону отрицательных значений [math]n[/math], причём единственным образом.
Применение
Расширенный треугольник Паскаля позволяет раскладывать в ряд простые дроби.
Например, [math]\dfrac{1}{(1+z)^2} = (1+z)^{-2} = \displaystyle\sum\limits_{k=0}^\infty\dbinom{-2}{k}z^k[/math].
В общем случае [math]\dfrac{1}{(1+z)^n} = (1+z)^{-n} = \displaystyle\sum\limits_{k=0}^\infty\dbinom{-n}{k}z^k[/math].
См. также
Источники информации
