Анализ временных рядов — различия между версиями
(→Краткое исследование данных) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 242 промежуточные версии 9 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Временные ряды {{---}} это актуальный инструмент | + | Временные ряды {{---}} это актуальный инструмент, применимый во множестве решений, от предсказания цен на акции, прогнозов погоды, планирования бизнеса, до распределения ресурсов. Несмотря на то, что прогнозирование может быть сведено к построению контролируемой [[Вариации регрессии|регрессии]], существуют особенности, связанные с временным характером наблюдений, которые необходимо учитывать, используя специальные инструменты.<br> |
==Временной ряд== | ==Временной ряд== | ||
| − | + | <br> | |
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Временно́й ряд (или ряд динамики)''' {{---}} собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом. Во временном ряде для каждого отсчёта должно быть указано время измерения или номер измерения по порядку. | ||
| + | }} | ||
| − | + | Как и большинство других видов анализа, анализ временных рядов предполагает, что данные содержат систематическую составляющую (обычно включающую несколько компонент) и случайный шум (ошибку), который затрудняет обнаружение регулярных компонент. Большинство методов исследования временных рядов включает различные способы фильтрации шума, позволяющие увидеть регулярную составляющую более отчетливо. Большинство регулярных составляющих временных рядов принадлежит к двум классам: они являются либо трендом, либо сезонной составляющей. Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая {{---}} это периодически повторяющаяся компонента. Оба эти вида регулярных компонент часто присутствуют в ряде одновременно. | |
| − | |||
| − | |||
| − | + | ==Валидирование и тестирование модели временного ряда== | |
| + | <br> | ||
| + | Данные упорядочены относительно неслучайных моментов времени, и, значит, в отличие от случайных выборок, могут содержать в себе дополнительную информацию, поэтому нельзя пользоваться обычными способами валидации. Чтобы избежать смещения оценки необходимо удостовериться, что обучающие наборы данных содержат только наблюдения, которые произошли до событий из валидирующиx наборов.<br> | ||
| + | [[Файл:TimeSeriesCross-validation.png |thumb|left|400px|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 1.] Кросс-валидация временного ряда]]<br> | ||
| − | + | Возможным способом преодоления данной проблемы будет использование скользящего окна, как описано [https://robjhyndman.com/hyndsight/tscv/ здесь]. Эта процедура называется [[Кросс-валидация|кросс-валидацией]] временного ряда и может быть вкратце описана следующей картинкой (рис. 1), в которой синие точки обозначают тренировочный набор данных, а красные соответствующие валидационные наборы данных.<br> | |
| − | Определив лучшую модель, | + | Если необходимо предсказать следующие $n$ шагов, то можно заранее кросс-валидировать $1,2,...,n$.<br> Таким образом можно также сравнить качество предсказаний для разных временных горизонтов.<br><br> |
| + | |||
| + | Определив лучшую модель, можно применить её ко всему обучающему набору и оценить его работу на следующем во времени наборе данных. Оценка работы может быть дана с использованием метода скользящего окна<ref>[https://wiki.loginom.ru/articles/windowing-method.html loginom: Метод скользящего окна]</ref>, который используем при кросс-валидации, но без переподсчёта параметра модели. | ||
==Краткое исследование данных== | ==Краткое исследование данных== | ||
| − | [[Файл:ManufactureOfElectricalEquipment.png|thumb| | + | [[Файл:ManufactureOfElectricalEquipment.png|thumb|right|300px|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 2.] Набор данных описывающий график производства электрооборудования]]<br> |
| − | |||
| − | |||
| − | + | В данной части используется несколько разных моделей для предсказания изменений в промышленном производстве,<br> которые для примера будем оценивать численно, как количество электрооборудования, произведённого в зоне Евро (рис. 2, 3).<br> | |
| + | [[Файл:SeasonalPlotMonthluSeasonalPattern.png|thumb|right|300px|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 3.] Сезонные колебания]] | ||
| + | Набор данных описывает ежемесячное производство электрооборудования (компьютеры электрические и оптические приборы) в зоне евро (17 стран) в период с января 1996 по март 2012 года (см. график ниже). Последние два года будем использовать при тестировании.<br><br><br><br><br> | ||
| − | + | ==Модели прогнозирования временных рядов== | |
| − | |||
| − | + | Существует 10 моделей прогнозирования, у каждой имеются свои достоинства и недостатки. Ниже, используя каждую модель, предскажем 12 месяцев, соответственно, значение $t+1, t+2, …, t + 12$. | |
| + | Имеет смысл использовать среднюю абсолютную ошибку для работы оценки модели.<br><br><br> | ||
| + | ===Наивное предсказание=== | ||
| + | [[Файл:NaiveElectricalEquipmentManufacturing.png|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 4.] Наивная]]<br> | ||
| + | Предсказания для каждого горизонта соотвествуют последнему наблюдаемому значению | ||
| + | $Y(t + h|t) = Y(t)$. | ||
| − | + | Такие предскания предполагают, что стохастическая<ref>[https://ru.wikipedia.org/wiki/Стохастичность Википедия: Стохастичность]</ref> модель генерирует [[Участник:Mk17.ru|случайное блуждание]].<br> | |
| + | [[Файл:SeasonalNaiveElectricalEquipmentManufacturing.png|thumb|left|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 5.] Cезонно-наивная]]<br> | ||
| + | Расширение наивной модели сезонно-наивная модель (англ. Season Naive, SNAIVE) {{---}} сезонно-наивная модель предполагает, что временной ряд имеет сезонную компоненту, и что период сезонности $T$.<br> | ||
| − | |||
| + | Прогнозы SNAIVE-модели описываются формулой $\dot{Y}(t+h|t) = Y(t+h-T)$. | ||
| + | Получаемые прогнозы следующие $T$ шагов совпадают с предыдущими $T$ шагами. | ||
| + | Эти модели часто используются как ориентировочные модели. Следующий графики показывают предсказания двух моделей для 2007 года (рис. 4, 5).<br><br> | ||
| − | + | ===Разделение по сезонам + любая модель=== | |
| + | [[Файл:STL_docompositionOnIndustrialProductionIndexData.png|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 6.] Методы разложения ряда]]<br> | ||
| + | Если данные показывают, что они восприимчивы к периодическим (сезонным) изменениям (ежедневно, еженедельно, ежеквартально, ежегодно), то будет полезным разложить исходный временной ряд на сумму трёх компонентов.<br> | ||
| − | = | + | $Y(t) = S(t) + T(t) + R(t)$<br> |
| − | + | $S(t)$ {{---}} сезонный компонент.<br> | |
| − | + | $T(t)$ {{---}} компонент трендового цикла.<br> | |
| − | + | $R(t)$ {{---}} остаток.<br> | |
| − | + | Существуют несколько способов для такого разложения, но наиболее простой называется классическим разложением и заключается в том, чтобы оценить тренд $T(t)$ через скользящее среднее, посчитать $S(t)$, как среднее без тренда $Y(t) - T(t)$ для каждого сезона.<br> | |
| − | + | Посчитать остаток, как $R(t) = Y(t) - T(t)-S(t)$.<br> | |
| − | + | [[Файл:SeasonallyAdjustedIndustrial.png |thumb|left|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 7.] Сезонные индексы ряда]] | |
| − | + | Классическое разложение можно расширить несколькими способами.<br> | |
| − | + | Расширение позволяет использовать данный метод при: | |
| − | + | * непостоянной величине сезона; | |
| − | + | * посчитать начальные и конечные значения декомпозиции; | |
| + | * избежать лишнего сглаживания; | ||
| − | + | Обзор методов разложений ряда можно увидеть по [https://otexts.com/fpp2/decomposition.html ссылке]. Используется реализация из стандартной библиотеки (рис. 6).<br> | |
| − | + | Одним из способов использования декомпозиции для прогнозирования будет:<br> | |
| + | 1) Разложить обучающий набор алгоритмом.<br> | ||
| + | 2) Посчитать сезонное отклонение ряда $Y(t) - S(t)$, используя любую модель для прогнозирования сезонно-чувствительного временного ряда.<br> | ||
| + | 3) Добавить прогнозам сезонность последнего временного периода во временном ряду (в нашем случае $S(t)$ для прошлого года).<br> | ||
| + | [[Файл:SeasonallyAdjustedTimeSeries.png|right|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 8.] Декомпозиция и наивная модель]]<br> | ||
| + | На следующем графике показаны сезонные индексы ряда с учётом сезонности (рис. 7). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Следующий график показывает расчёты для 2007 года с использованием декомпозиции и наивной модели (рис. 8) для сезонно-изменяемого временного ряда.<br> | |
| − | |||
| − | + | ===Экспоненциальное сглаживание === | |
| − | + | <br> | |
| + | [[Файл:ExpSmoothing.png|thumb|left|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 9.] Данные полученные для 2007 года с использованием модели экспоненциального сглаживания]] | ||
| + | Экспоненциальное сглаживание<ref>[https://ru.wikipedia.org/wiki/Экспоненциальное_сглаживание Википедия: Экспоненциальное сглаживание]</ref> {{---}} один из наиболее успешных классических методов предсказаний. В своей базовой форме он называется простым экспоненциальный сглаживанием и его прогнозы описываются формулами: | ||
| + | $Ŷ(t+h|t) = ⍺y(t) + ⍺(1-⍺)y(t-1) + ⍺(1-⍺)²y(t-2) + …$<br> | ||
| + | где''''' $0<⍺<1$ '''''. Если $⍺ = 0$, то текущие наблюдения игнорируются, если же $⍺ = 1$, то полностью игнорируются предыдущие наблюдения.<br> | ||
| + | [[Файл:ExpSmoothing+Decomposition.png|thumb|right|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 10.] Данные полученные для 2007 года, с использованием модели экспоненциального сглаживания и декомпозиции]] | ||
| − | + | Заметно, что прогнозы равны взвешенному среднему от старых наблюдений, и что соответствующие веса убывают экспоненциально по мере хода времени. | |
| − | + | Некоторые методы для расширения алгоритма позволяют добавить тренд, его затухание и сезонность. | |
| + | Экспоненциальное сглаживание состоит из 9 моделей, которые подробно описаны [https://otexts.com/fpp2/taxonomy.html здесь]. | ||
| − | + | Следующие графики (рис. 9, 10) описывают прогнозы данных полученные для 2007 года, с использованием модели экспоненциального сглаживания (выбраны автоматически), которые подходили исходному и сезонно-чувствительному временному ряду.<br> | |
| − | |||
| − | + | ===ARIMA, SARIMA=== | |
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| − | + | [[Файл:SARIMA.png |thumb|left|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 11.] SARIMA]] | |
| − | + | Также как и экспоненциальное сглаживание, интегрированная модель авторегрессии скользящего среднего (англ. autoregressive integrated moving average, ARIMA) также часто используются для прогноза временных рядов. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{Определение | |
| − | + | |definition = | |
| + | '''Процесс авторегрессии''' {{---}} последовательная зависимость элементов временного ряда, выразается следующим уравнением: | ||
| + | $x(t) = \psi + \phi_1 * x_(t-1) + \phi_2 * x_(t-2) + \phi_3 * x_(t-3) + ... + \epsilon$<br> | ||
| + | Где $\psi$ {{---}} свободный член (константа).<br> | ||
| + | $\phi_1, \phi_2, \phi_3, ...$ {{---}} параметры авторегрессии. | ||
| + | }} | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Скользящее среднее''' {{---}} общее название для семейства функций, значения которых в каждой точке определения равны некоторому среднему значению исходной функции за предыдущий период. | ||
| + | }} | ||
| − | + | {{Определение | |
| − | [[Файл: | + | |definition = |
| − | + | '''Процесс скользящего среднего''' {{---}} в процессе скользящего среднего каждый элемент ряда подвержен суммарному воздействию предыдущих ошибок. В общем виде это можно записать следующим образом: | |
| + | $x_t = \mu + \epsilon_t - \theta_1 * \epsilon_{t-1} - \theta_2 * \epsilon_{t-2} - ...$ <br> | ||
| + | Где $\mu$ {{---}} константа.<br> | ||
| + | $\theta_1, \theta_2, \theta_3, ...$ {{---}} параметры скользящего среднего. | ||
| + | }} | ||
| + | [[Файл:SARIMA_Decomposition.png|thumb|right|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 12.] SARIMA декомпозированная]] | ||
| + | ARIMA {{---}} комбинация этих двух подходов. Так как эти подходы требуются стационарности временного ряда, может понадобится продифференциировать/проинтегрировать ряд. | ||
| + | То есть рассматировать ряд разностей, а не исходный ряд. | ||
| − | + | Сезонная интегрированная модель авторегрессии скользящего среднего (англ. season autoregressive integrated moving average, SARIMA) учитывает сезонность, добавляя линейную комбинацию прошлых сезонных значений и/или прошлых ошибок прогноза. | |
| − | + | Более подробную информацию про ARIMA, SARIMA читайте по [https://otexts.com/fpp2/arima.html ссылке]. | |
| − | |||
| − | |||
| − | + | Данные графики показывают предсказания полученные для 2007 года, с использованием модели SARIMA (рис. 11,12). | |
| − | + | ===Garch=== | |
| − | + | <br> | |
| + | [[Файл:GARCH.png |thumb|left|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 13.] ARMA]]<br> | ||
| − | + | В предыдущих моделях считалось, что слагаемое ошибки в стохастическом процессе генерации временного ряда имело одинаковую дисперсию. | |
| − | + | В GARСH-модели (англ. Generalized AutoRegressive Conditional Heteroscedasticity, GARCH) предполагается, что слагаемое ошибки следует авторегрессионному скользящему среднему (англ. AutoRegressive Moving Average, ARMA), соответственно слагаемое меняется по ходу времени. Это особенно полезно при моделировании финансовых временных рядов, так как диапазон изменений тоже постоянно меняется (рис. 13). | |
| − | |||
| − | |||
| − | + | В 1982 году была предложена ARCH {{---}} модель, описываемая формулой: <br> | |
| − | |||
| − | + | $\sigma^2(t) = \alpha + \sum_{i = 1}^{\alpha}b_ir^{2}_{t-1}$ <br> | |
| − | + | где $\alpha$ {{---}} коэффициент задержки<br> | |
| + | $\sigma^2(t)$ - волатильность<br> | ||
| + | $\sum_{i = 1}^{\alpha}b_ir^{2}_{t-1}$ - линенйная комбинация абсолютных значений нескольких последних изменений значений. | ||
| − | + | Позднее была создана GARCH {{---}} обобщённая ARCH модель, которая также учитывает предыдущие оценки дисперсии. Формула может быть записана так: | |
| − | + | $\sigma^2(t) = \alpha + \sum_{i = 1}^{\alpha}b_ir^{2}_{t-1} \sum_{i = 1}^{p}c_i\sigma^{2}_{t-1}$ <br> | |
| + | где p {{---}} количество предшествующих оценок, влияющих на текущее значение.<br> | ||
| + | с {{---}} весовые коэффициенты предыдущих оценок. | ||
| − | + | Обычно ARMA используется и для учёта среднего, более подробное введение в Garsh и различные варианты можно найти [https://cran.r-project.org/web/packages/rugarch/vignettes/Introduction_to_the_rugarch_package.pdf здесь].<br><br> | |
| − | |||
| − | + | ===Динамические линейные модели=== | |
| − | [[Файл: | + | [[Файл:DLM+Decomposition.png|right|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 14.] DLM]]<br> |
| − | + | Динамические линейные модели представляют другой класс моделей предсказания временных рядов (рис. 14). | |
| + | Идея заключается в том, что в каждый момент времени $t$ эти модели соответствуют линейной модели, но коэффициент регрессии постоянно меняется. <br>Пример динамической линейной модели ниже:<br> | ||
| + | $y(t) = ⍺(t) + tβ(t) + w(t)$,<br> | ||
| + | $⍺(t) = ⍺(t-1) + m(t)$,<br> | ||
| + | $β(t) = β(t-1) + r(t)$,<br> | ||
| + | $w(t)$ ~ $N(0,W)$, $m(t)$ ~ $N(0,M)$, $r(t)$ ~ $N(0,R)$.<br> | ||
| − | + | В предыдущей модели коэффициенты $a(t)$ и $b(t)$ следуют случайному блужданию. | |
| − | + | Динамические линейные модели могут быть построены в рамках Байесовской системы. Тем не менее и этот метод можно улучшить, подробности [https://cran.r-project.org/web/packages/dlm/vignettes/dlm.pdf здесь].<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===TBATS=== | ===TBATS=== | ||
| − | + | <br> | |
| + | [[Файл:TBATS_Electrical.png |left|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 15.] DLM]] | ||
| + | TBATS (англ. Trigonometric seasonality, Box-Cox transformation, ARMA errors, Trend and Seasonal components) {{---}} это модели, которые основаны на экспоненциальном сглаживании (рис. 15).<br> Главной особенностью TBATS является возможность взаимодействия с несколькими сезонностями. Моделируя каждую функцию сезонности отдельным тригонометрическим отображением построенным на [[L 2-теория рядов Фурье|рядах Фурье]]. <br><br>Классическим примером комплексной сезонности будет отображение ежедневных объемов продаж, которое имеет, как еженедельные колебания, так и ежегодные.<br> | ||
| − | Больше информации можно прочиать [https://robjhyndman.com/papers/ComplexSeasonality.pdf тут].<br> | + | Больше информации можно прочиать [https://robjhyndman.com/papers/ComplexSeasonality.pdf тут].<br><br><br> |
| − | |||
===Prophet=== | ===Prophet=== | ||
| − | Ещё одна модель, способная взаимодействовать с несколькими сезонностями. | + | <br> |
| − | Это ПО с открытым исходным кодом от Фейсбука.<br> | + | Ещё одна модель, способная взаимодействовать с несколькими сезонностями (рис. 16). |
| − | Prophet считает, что временной ряд может быть | + | Это ПО с открытым исходным кодом от Фейсбука ([https://facebook.github.io/prophet/ ссылка]).<br> |
| − | + | [[Файл:Prophet.png |right|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 16.] Prophet]] | |
| − | g(t) {{---}} тренд<br> | + | |
| − | s(t) {{---}} сезонность<br> | + | Prophet считает, что временной ряд может быть разложен следующим образом:<br> |
| − | h(t) {{---}} каникулы<br> | + | $y(t) = g(t) + s(t) + h(t) + ε(t)$,<br> |
| − | ε(t) {{---}} ошибки<br> | + | $g(t)$ {{---}} тренд,<br> |
| + | $s(t)$ {{---}} сезонность,<br> | ||
| + | $h(t)$ {{---}} каникулы, т.е аномальные данные,<br> | ||
| + | $ε(t)$ {{---}} ошибки.<br> | ||
Подгонка модели представляет собой упражнение по подгонке кривой, поэтому она явно не учитывает структуру временной зависимости в данных. Это также позволяет проводить наблюдения с нерегулярным интервалом.<br> | Подгонка модели представляет собой упражнение по подгонке кривой, поэтому она явно не учитывает структуру временной зависимости в данных. Это также позволяет проводить наблюдения с нерегулярным интервалом.<br> | ||
| − | Есть два варианта временных рядов тренда: модель насыщающего роста и кусочно-линейная модель. Модель многопериодной сезонности основана на рядах Фурье. Эффект известных и заказных выходных дней может быть легко включен в модель.<br> | + | Есть два варианта временных рядов тренда: модель насыщающего роста и кусочно-линейная модель. Модель многопериодной сезонности основана на рядах Фурье<ref>[[Определение ряда Фурье]]</ref>. Эффект известных и заказных выходных дней может быть легко включен в модель.<br> |
| − | Модель | + | Модель Prophet вставлена в байесовскую структуру и позволяет сделать полный апостериорный вывод, чтобы включить неопределенность параметров модели в неопределенность прогноза.<br> |
| − | |||
===NNETAR=== | ===NNETAR=== | ||
| − | Модель NNETAR представляет собой | + | <br> |
| + | [[Файл:NNETARElectriacalequipmntManufacturing.png |left|300px|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 17.] NNETAR]] | ||
| + | Модель авторегрессии нейронной сети (англ. Neural NETwork AutoRegression, NNETAR) представляет собой полносвязную [https://neerc.ifmo.ru/wiki/index.php?title=Нейронные_сети,_перцептрон нейронную сеть]. | ||
| + | Модель NNETAR принимает на вход последние элементы последовательности до момента времени $t$ и выводит прогнозируемое значение в момент времени $t + 1$. Для выполнения многоэтапных прогнозов сеть применяется итеративно. | ||
| + | |||
| + | Модель можно описать уравнением | ||
| + | $y_t = f(y_{t-1}) + \epsilon_t$ <br> | ||
| + | где $y_{t-1} = (y_{t-1}, y_{t-2}, ...)'$ {{---}} вектор, содержащий запаздывающие значения, <br> | ||
| + | f {{---}} нейронная сеть, с 4 скрытыми узлами в каждом слое, <br> | ||
| + | $\epsilon_t$ {{---}} считаем, что ряд ошибок [https://ru.wikipedia.org/wiki/Гомоскедастичность гомокседастичен] (и возможно имеет нормальное распределение).<br> | ||
| + | [[Файл:NNETARElectriacalequipmntManufacturingDecomposition.png |right|300px|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 18.] NNETAR c декомпозицией]] | ||
| + | |||
| + | Мы можем моделировать будущие выборочные пути этой модели итеративно, случайным образом генерируя значение для $\epsilon_t$ либо из нормального распределения, либо путем повторной выборки из исторических значений.<br> Так что если | ||
| + | $\epsilon^*_{T+1}$ | ||
| + | {{---}} случайная выборка из распределения ошибок в момент времени $T+1$,<br> тогда $y^*_{T+1} = f(y_T) + \epsilon^*_{T+1}$ {{---}} один из возможных вариантов распределения прогнозов для $y_{T+1}$ <br> | ||
| + | Установив $y^*_{T+1} = (y^*_{T+1}, y_{T})'$, мы можем повторить процесс, чтобы получить $y^*_{T+2} = f(y_{T+1}) + \epsilon_{T+2}$. <br> | ||
| − | + | Таким образом, мы можем итеративно моделировать будущий путь выборки. Повторно моделируя выборочные пути, мы накапливаем знания о распределении всех будущих значений на основе подобранной нейронной сети. | |
===LSTM=== | ===LSTM=== | ||
| − | + | <br> | |
| + | Блок [[:Долгая_краткосрочная_память|cети долго-краткосрочной памяти]] (англ. Long short-term memory, LSTM) могут использоваться для прогнозирования временных рядов (а также других рекуррентных нейронных сетей). <br> | ||
Состояние сети LSTM представлено через вектор пространства состояний. Этот метод позволяет отслеживать зависимости новых наблюдений от прошлых (даже очень далеких).<br> | Состояние сети LSTM представлено через вектор пространства состояний. Этот метод позволяет отслеживать зависимости новых наблюдений от прошлых (даже очень далеких).<br> | ||
| − | Вообще говоря, LSTM представляют собой сложные модели, и они редко используются для прогнозирования одного временного ряда, поскольку для их оценки требуется большой объем данных.<br>Однако они обычно используются, когда необходимы прогнозы для большого количества временных рядов( | + | Вообще говоря, LSTM представляют собой сложные модели, и они редко используются для прогнозирования одного временного ряда, поскольку для их оценки требуется большой объем данных.<br>Однако они обычно используются, когда необходимы прогнозы для большого количества временных рядов (как показано [https://arxiv.org/abs/1704.04110 здесь]). |
==Оценка== | ==Оценка== | ||
| − | + | [[Файл:Evaluation.png |right|600px|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 19.] MAE с перекрестной проверкой для каждой модели]] | |
| − | На следующем рисунке | + | Выполнен выбор модели с помощью процедуры перекрестной проверки, описанной ранее. Не рассчитывая его для динамических линейных моделей и моделей LSTM из-за их высокой вычислительной стоимости и низкой производительности.<br> |
| − | + | На следующем рисунке показана [[Оценка качества в задачах классификации и регрессии|средняя абсолютная ошибка]] (англ. Mean Absolute Error, MAE) с перекрестной проверкой для каждой модели и для каждого временного горизонта (рис. 17): | |
| − | + | Модель NNETAR по сезонно скорректированным данным была лучшей моделью для данной задачи, поскольку она соответствовала самому низкому значению MAE, прошедшему перекрестную проверку.<br> | |
| + | Чтобы получить объективную оценку наилучшей производительности модели, вычислим MAE на тестовом наборе (рис. 18), получив оценку, равную 5,24. На следующем рисунке можно увидеть MAE, оцененную на тестовой выборке для каждого временного горизонта.<br> | ||
| − | + | [[Файл:Cross-validated MAE.png |left|thumb|[https://towardsdatascience.com/an-overview-of-time-series-forecasting-models-a2fa7a358fcb Рисунок 20.] MAE, тестовый набор]] | |
| − | + | <br><br><br> | |
| − | [[Файл:Cross-validated MAE.png]]<br> | + | === Методы увеличения производительности=== |
| − | + | *Использование разных моделей для разных временных горизонтов, | |
| − | + | *Объединение нескольких прогнозов (например, с учетом среднего прогноза), | |
| − | *Использование разных моделей для разных временных горизонтов | + | *Агрегация начальных данных. |
| − | *Объединение нескольких прогнозов (например, с учетом среднего прогноза) | + | <br><br><br> |
| − | * | ||
| − | <br><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Заключительные замечания== | ==Заключительные замечания== | ||
| − | + | Большинство ранее описанных моделей позволяют легко включать изменяющиеся во времени предикторы. Они могут быть извлечены из одного и того же временного ряда или могут соответствовать внешним предикторам (например, временному ряду другого индекса). В последнем случае необходимо обратить внимание на то, чтобы не использовать информацию из будущего, которая могла бы быть удовлетворена путем прогнозирования предикторов или использования версий c ошибками.<br> | |
| − | + | Обратите внимание, что в данном конспекте рассматривается случай, когда у нас есть один временной ряд для прогнозирования. Когда у нас много временных рядов, может быть предпочтительнее глобальный подход, поскольку он позволяет нам оценивать более сложную и потенциально более точную модель. Подробнее о глобальном подходе [https://arxiv.org/abs/1704.04110 здесь]. | |
| − | |||
==См. Также== | ==См. Также== | ||
* [[Кластеризация]] | * [[Кластеризация]] | ||
| Строка 220: | Строка 240: | ||
* [[Рекомендательные системы]] | * [[Рекомендательные системы]] | ||
* [[Анализ социальных сетей]] | * [[Анализ социальных сетей]] | ||
| + | * [[Графовые нейронные сети]] | ||
| + | * [[Компьютерное зрение]] | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
==Источники Информации== | ==Источники Информации== | ||
| − | * | + | *[http://www.machinelearning.ru/wiki/index.php?title=Временной_ряд machinelearning.ru] |
| − | * | + | *[https://ru.wikipedia.org/wiki/Временной_ряд Википедия: Временной ряд] |
| − | + | *[http://statsoft.ru/home/textbook/modules/sttimser.html StatSoft: Анализ временных рядов] | |
| + | *[https://chaos.phys.msu.ru/loskutov/PDF/Lectures_time_series_analysis.pdf Лоскутов А.Ю. физ. фак. МГУ: Анализ Временных Рядов] | ||
| + | *[https://wiki.loginom.ru/articles/garch-model.html loginom: Garch-модель] | ||
| + | *[https://otexts.com/fpp2/nnetar.html Otexts: NNETAR] | ||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
[[Категория: Анализ временных рядов]] | [[Категория: Анализ временных рядов]] | ||
Текущая версия на 19:11, 4 сентября 2022
Временные ряды — это актуальный инструмент, применимый во множестве решений, от предсказания цен на акции, прогнозов погоды, планирования бизнеса, до распределения ресурсов. Несмотря на то, что прогнозирование может быть сведено к построению контролируемой регрессии, существуют особенности, связанные с временным характером наблюдений, которые необходимо учитывать, используя специальные инструменты.
Содержание
Временной ряд
| Определение: |
| Временно́й ряд (или ряд динамики) — собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом. Во временном ряде для каждого отсчёта должно быть указано время измерения или номер измерения по порядку. |
Как и большинство других видов анализа, анализ временных рядов предполагает, что данные содержат систематическую составляющую (обычно включающую несколько компонент) и случайный шум (ошибку), который затрудняет обнаружение регулярных компонент. Большинство методов исследования временных рядов включает различные способы фильтрации шума, позволяющие увидеть регулярную составляющую более отчетливо. Большинство регулярных составляющих временных рядов принадлежит к двум классам: они являются либо трендом, либо сезонной составляющей. Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая — это периодически повторяющаяся компонента. Оба эти вида регулярных компонент часто присутствуют в ряде одновременно.
Валидирование и тестирование модели временного ряда
Данные упорядочены относительно неслучайных моментов времени, и, значит, в отличие от случайных выборок, могут содержать в себе дополнительную информацию, поэтому нельзя пользоваться обычными способами валидации. Чтобы избежать смещения оценки необходимо удостовериться, что обучающие наборы данных содержат только наблюдения, которые произошли до событий из валидирующиx наборов.
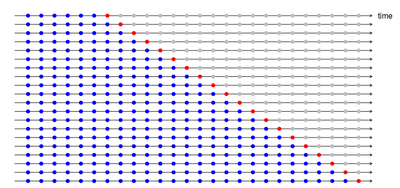
Возможным способом преодоления данной проблемы будет использование скользящего окна, как описано здесь. Эта процедура называется кросс-валидацией временного ряда и может быть вкратце описана следующей картинкой (рис. 1), в которой синие точки обозначают тренировочный набор данных, а красные соответствующие валидационные наборы данных.
Если необходимо предсказать следующие $n$ шагов, то можно заранее кросс-валидировать $1,2,...,n$.
Таким образом можно также сравнить качество предсказаний для разных временных горизонтов.
Определив лучшую модель, можно применить её ко всему обучающему набору и оценить его работу на следующем во времени наборе данных. Оценка работы может быть дана с использованием метода скользящего окна[1], который используем при кросс-валидации, но без переподсчёта параметра модели.
Краткое исследование данных
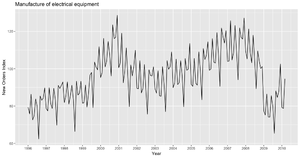
В данной части используется несколько разных моделей для предсказания изменений в промышленном производстве,
которые для примера будем оценивать численно, как количество электрооборудования, произведённого в зоне Евро (рис. 2, 3).
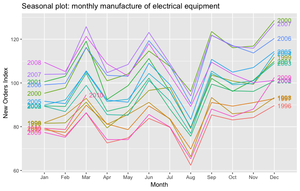
Набор данных описывает ежемесячное производство электрооборудования (компьютеры электрические и оптические приборы) в зоне евро (17 стран) в период с января 1996 по март 2012 года (см. график ниже). Последние два года будем использовать при тестировании.
Модели прогнозирования временных рядов
Существует 10 моделей прогнозирования, у каждой имеются свои достоинства и недостатки. Ниже, используя каждую модель, предскажем 12 месяцев, соответственно, значение $t+1, t+2, …, t + 12$.
Имеет смысл использовать среднюю абсолютную ошибку для работы оценки модели.
Наивное предсказание
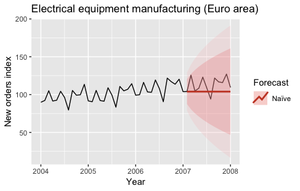
Предсказания для каждого горизонта соотвествуют последнему наблюдаемому значению $Y(t + h|t) = Y(t)$.
Такие предскания предполагают, что стохастическая[2] модель генерирует случайное блуждание.
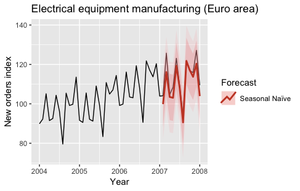
Расширение наивной модели сезонно-наивная модель (англ. Season Naive, SNAIVE) — сезонно-наивная модель предполагает, что временной ряд имеет сезонную компоненту, и что период сезонности $T$.
Прогнозы SNAIVE-модели описываются формулой $\dot{Y}(t+h|t) = Y(t+h-T)$.
Получаемые прогнозы следующие $T$ шагов совпадают с предыдущими $T$ шагами.
Эти модели часто используются как ориентировочные модели. Следующий графики показывают предсказания двух моделей для 2007 года (рис. 4, 5).
Разделение по сезонам + любая модель
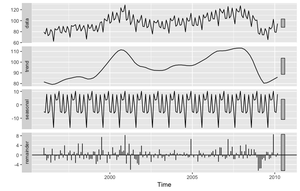
Если данные показывают, что они восприимчивы к периодическим (сезонным) изменениям (ежедневно, еженедельно, ежеквартально, ежегодно), то будет полезным разложить исходный временной ряд на сумму трёх компонентов.
$Y(t) = S(t) + T(t) + R(t)$
$S(t)$ — сезонный компонент.
$T(t)$ — компонент трендового цикла.
$R(t)$ — остаток.
Существуют несколько способов для такого разложения, но наиболее простой называется классическим разложением и заключается в том, чтобы оценить тренд $T(t)$ через скользящее среднее, посчитать $S(t)$, как среднее без тренда $Y(t) - T(t)$ для каждого сезона.
Посчитать остаток, как $R(t) = Y(t) - T(t)-S(t)$.
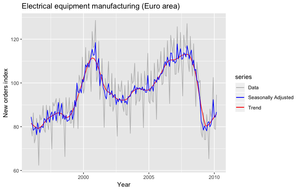
Классическое разложение можно расширить несколькими способами.
Расширение позволяет использовать данный метод при:
- непостоянной величине сезона;
- посчитать начальные и конечные значения декомпозиции;
- избежать лишнего сглаживания;
Обзор методов разложений ряда можно увидеть по ссылке. Используется реализация из стандартной библиотеки (рис. 6).
Одним из способов использования декомпозиции для прогнозирования будет:
1) Разложить обучающий набор алгоритмом.
2) Посчитать сезонное отклонение ряда $Y(t) - S(t)$, используя любую модель для прогнозирования сезонно-чувствительного временного ряда.
3) Добавить прогнозам сезонность последнего временного периода во временном ряду (в нашем случае $S(t)$ для прошлого года).
На следующем графике показаны сезонные индексы ряда с учётом сезонности (рис. 7).
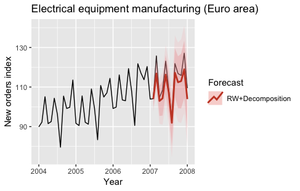
Следующий график показывает расчёты для 2007 года с использованием декомпозиции и наивной модели (рис. 8) для сезонно-изменяемого временного ряда.
Экспоненциальное сглаживание
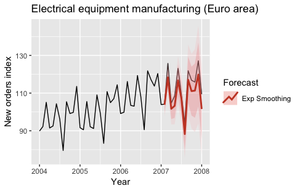
Экспоненциальное сглаживание[3] — один из наиболее успешных классических методов предсказаний. В своей базовой форме он называется простым экспоненциальный сглаживанием и его прогнозы описываются формулами:
$Ŷ(t+h|t) = ⍺y(t) + ⍺(1-⍺)y(t-1) + ⍺(1-⍺)²y(t-2) + …$
где $0<⍺<1$ . Если $⍺ = 0$, то текущие наблюдения игнорируются, если же $⍺ = 1$, то полностью игнорируются предыдущие наблюдения.
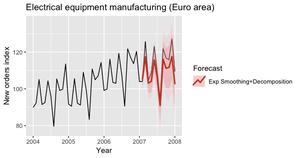
Заметно, что прогнозы равны взвешенному среднему от старых наблюдений, и что соответствующие веса убывают экспоненциально по мере хода времени.
Некоторые методы для расширения алгоритма позволяют добавить тренд, его затухание и сезонность. Экспоненциальное сглаживание состоит из 9 моделей, которые подробно описаны здесь.
Следующие графики (рис. 9, 10) описывают прогнозы данных полученные для 2007 года, с использованием модели экспоненциального сглаживания (выбраны автоматически), которые подходили исходному и сезонно-чувствительному временному ряду.
ARIMA, SARIMA
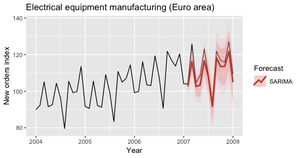
Также как и экспоненциальное сглаживание, интегрированная модель авторегрессии скользящего среднего (англ. autoregressive integrated moving average, ARIMA) также часто используются для прогноза временных рядов.
| Определение: |
| Процесс авторегрессии — последовательная зависимость элементов временного ряда, выразается следующим уравнением:
$x(t) = \psi + \phi_1 * x_(t-1) + \phi_2 * x_(t-2) + \phi_3 * x_(t-3) + ... + \epsilon$ |
| Определение: |
| Скользящее среднее — общее название для семейства функций, значения которых в каждой точке определения равны некоторому среднему значению исходной функции за предыдущий период. |
| Определение: |
| Процесс скользящего среднего — в процессе скользящего среднего каждый элемент ряда подвержен суммарному воздействию предыдущих ошибок. В общем виде это можно записать следующим образом:
$x_t = \mu + \epsilon_t - \theta_1 * \epsilon_{t-1} - \theta_2 * \epsilon_{t-2} - ...$ |
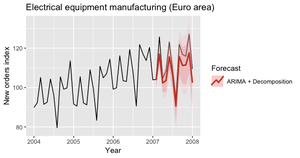
ARIMA — комбинация этих двух подходов. Так как эти подходы требуются стационарности временного ряда, может понадобится продифференциировать/проинтегрировать ряд. То есть рассматировать ряд разностей, а не исходный ряд.
Сезонная интегрированная модель авторегрессии скользящего среднего (англ. season autoregressive integrated moving average, SARIMA) учитывает сезонность, добавляя линейную комбинацию прошлых сезонных значений и/или прошлых ошибок прогноза. Более подробную информацию про ARIMA, SARIMA читайте по ссылке.
Данные графики показывают предсказания полученные для 2007 года, с использованием модели SARIMA (рис. 11,12).
Garch
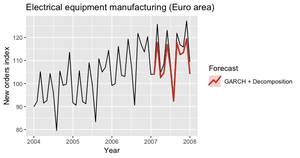
В предыдущих моделях считалось, что слагаемое ошибки в стохастическом процессе генерации временного ряда имело одинаковую дисперсию.
В GARСH-модели (англ. Generalized AutoRegressive Conditional Heteroscedasticity, GARCH) предполагается, что слагаемое ошибки следует авторегрессионному скользящему среднему (англ. AutoRegressive Moving Average, ARMA), соответственно слагаемое меняется по ходу времени. Это особенно полезно при моделировании финансовых временных рядов, так как диапазон изменений тоже постоянно меняется (рис. 13).
В 1982 году была предложена ARCH — модель, описываемая формулой:
$\sigma^2(t) = \alpha + \sum_{i = 1}^{\alpha}b_ir^{2}_{t-1}$
где $\alpha$ — коэффициент задержки
$\sigma^2(t)$ - волатильность
$\sum_{i = 1}^{\alpha}b_ir^{2}_{t-1}$ - линенйная комбинация абсолютных значений нескольких последних изменений значений.
Позднее была создана GARCH — обобщённая ARCH модель, которая также учитывает предыдущие оценки дисперсии. Формула может быть записана так:
$\sigma^2(t) = \alpha + \sum_{i = 1}^{\alpha}b_ir^{2}_{t-1} \sum_{i = 1}^{p}c_i\sigma^{2}_{t-1}$
где p — количество предшествующих оценок, влияющих на текущее значение.
с — весовые коэффициенты предыдущих оценок.
Обычно ARMA используется и для учёта среднего, более подробное введение в Garsh и различные варианты можно найти здесь.
Динамические линейные модели
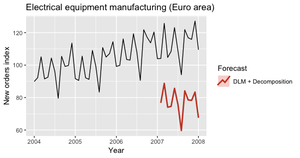
Динамические линейные модели представляют другой класс моделей предсказания временных рядов (рис. 14).
Идея заключается в том, что в каждый момент времени $t$ эти модели соответствуют линейной модели, но коэффициент регрессии постоянно меняется.
Пример динамической линейной модели ниже:
$y(t) = ⍺(t) + tβ(t) + w(t)$,
$⍺(t) = ⍺(t-1) + m(t)$,
$β(t) = β(t-1) + r(t)$,
$w(t)$ ~ $N(0,W)$, $m(t)$ ~ $N(0,M)$, $r(t)$ ~ $N(0,R)$.
В предыдущей модели коэффициенты $a(t)$ и $b(t)$ следуют случайному блужданию.
Динамические линейные модели могут быть построены в рамках Байесовской системы. Тем не менее и этот метод можно улучшить, подробности здесь.
TBATS
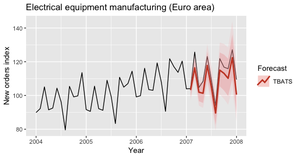
TBATS (англ. Trigonometric seasonality, Box-Cox transformation, ARMA errors, Trend and Seasonal components) — это модели, которые основаны на экспоненциальном сглаживании (рис. 15).
Главной особенностью TBATS является возможность взаимодействия с несколькими сезонностями. Моделируя каждую функцию сезонности отдельным тригонометрическим отображением построенным на рядах Фурье.
Классическим примером комплексной сезонности будет отображение ежедневных объемов продаж, которое имеет, как еженедельные колебания, так и ежегодные.
Больше информации можно прочиать тут.
Prophet
Ещё одна модель, способная взаимодействовать с несколькими сезонностями (рис. 16).
Это ПО с открытым исходным кодом от Фейсбука (ссылка).
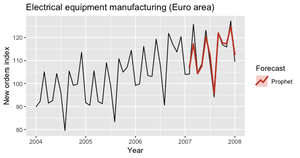
Prophet считает, что временной ряд может быть разложен следующим образом:
$y(t) = g(t) + s(t) + h(t) + ε(t)$,
$g(t)$ — тренд,
$s(t)$ — сезонность,
$h(t)$ — каникулы, т.е аномальные данные,
$ε(t)$ — ошибки.
Подгонка модели представляет собой упражнение по подгонке кривой, поэтому она явно не учитывает структуру временной зависимости в данных. Это также позволяет проводить наблюдения с нерегулярным интервалом.
Есть два варианта временных рядов тренда: модель насыщающего роста и кусочно-линейная модель. Модель многопериодной сезонности основана на рядах Фурье[4]. Эффект известных и заказных выходных дней может быть легко включен в модель.
Модель Prophet вставлена в байесовскую структуру и позволяет сделать полный апостериорный вывод, чтобы включить неопределенность параметров модели в неопределенность прогноза.
NNETAR
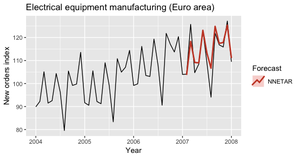
Модель авторегрессии нейронной сети (англ. Neural NETwork AutoRegression, NNETAR) представляет собой полносвязную нейронную сеть. Модель NNETAR принимает на вход последние элементы последовательности до момента времени $t$ и выводит прогнозируемое значение в момент времени $t + 1$. Для выполнения многоэтапных прогнозов сеть применяется итеративно.
Модель можно описать уравнением
$y_t = f(y_{t-1}) + \epsilon_t$
где $y_{t-1} = (y_{t-1}, y_{t-2}, ...)'$ — вектор, содержащий запаздывающие значения,
f — нейронная сеть, с 4 скрытыми узлами в каждом слое,
$\epsilon_t$ — считаем, что ряд ошибок гомокседастичен (и возможно имеет нормальное распределение).
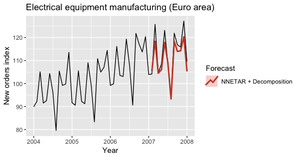
Мы можем моделировать будущие выборочные пути этой модели итеративно, случайным образом генерируя значение для $\epsilon_t$ либо из нормального распределения, либо путем повторной выборки из исторических значений.
Так что если
$\epsilon^*_{T+1}$
— случайная выборка из распределения ошибок в момент времени $T+1$,
тогда $y^*_{T+1} = f(y_T) + \epsilon^*_{T+1}$ — один из возможных вариантов распределения прогнозов для $y_{T+1}$
Установив $y^*_{T+1} = (y^*_{T+1}, y_{T})'$, мы можем повторить процесс, чтобы получить $y^*_{T+2} = f(y_{T+1}) + \epsilon_{T+2}$.
Таким образом, мы можем итеративно моделировать будущий путь выборки. Повторно моделируя выборочные пути, мы накапливаем знания о распределении всех будущих значений на основе подобранной нейронной сети.
LSTM
Блок cети долго-краткосрочной памяти (англ. Long short-term memory, LSTM) могут использоваться для прогнозирования временных рядов (а также других рекуррентных нейронных сетей).
Состояние сети LSTM представлено через вектор пространства состояний. Этот метод позволяет отслеживать зависимости новых наблюдений от прошлых (даже очень далеких).
Вообще говоря, LSTM представляют собой сложные модели, и они редко используются для прогнозирования одного временного ряда, поскольку для их оценки требуется большой объем данных.
Однако они обычно используются, когда необходимы прогнозы для большого количества временных рядов (как показано здесь).
Оценка
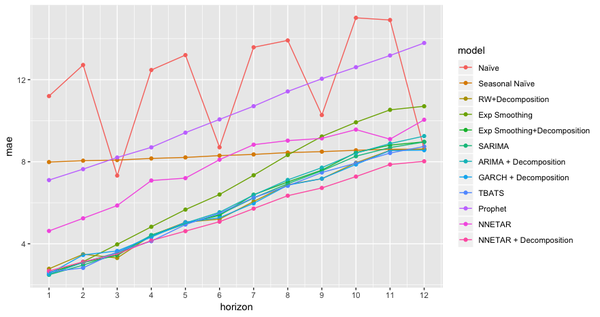
Выполнен выбор модели с помощью процедуры перекрестной проверки, описанной ранее. Не рассчитывая его для динамических линейных моделей и моделей LSTM из-за их высокой вычислительной стоимости и низкой производительности.
На следующем рисунке показана средняя абсолютная ошибка (англ. Mean Absolute Error, MAE) с перекрестной проверкой для каждой модели и для каждого временного горизонта (рис. 17):
Модель NNETAR по сезонно скорректированным данным была лучшей моделью для данной задачи, поскольку она соответствовала самому низкому значению MAE, прошедшему перекрестную проверку.
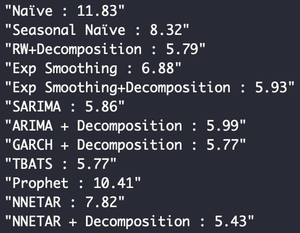
Чтобы получить объективную оценку наилучшей производительности модели, вычислим MAE на тестовом наборе (рис. 18), получив оценку, равную 5,24. На следующем рисунке можно увидеть MAE, оцененную на тестовой выборке для каждого временного горизонта.
Методы увеличения производительности
- Использование разных моделей для разных временных горизонтов,
- Объединение нескольких прогнозов (например, с учетом среднего прогноза),
- Агрегация начальных данных.
Заключительные замечания
Большинство ранее описанных моделей позволяют легко включать изменяющиеся во времени предикторы. Они могут быть извлечены из одного и того же временного ряда или могут соответствовать внешним предикторам (например, временному ряду другого индекса). В последнем случае необходимо обратить внимание на то, чтобы не использовать информацию из будущего, которая могла бы быть удовлетворена путем прогнозирования предикторов или использования версий c ошибками.
Обратите внимание, что в данном конспекте рассматривается случай, когда у нас есть один временной ряд для прогнозирования. Когда у нас много временных рядов, может быть предпочтительнее глобальный подход, поскольку он позволяет нам оценивать более сложную и потенциально более точную модель. Подробнее о глобальном подходе здесь.
См. Также
- Кластеризация
- Уменьшение размерности
- Рекомендательные системы
- Анализ социальных сетей
- Графовые нейронные сети
- Компьютерное зрение