|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | '''Алгоритм Прима''' (англ. ''Prim's algorithm'') — алгоритм поиска [[Лемма о безопасном ребре#Минимальное остовное дерево|минимального остовного дерева]] (англ. ''minimum spanning tree, MST'') во взвешенном [[Основные определения теории графов#Неориентированные графы | неориентированном связном графе]]. | | '''Алгоритм Прима''' (англ. ''Prim's algorithm'') — алгоритм поиска [[Лемма о безопасном ребре#Минимальное остовное дерево|минимального остовного дерева]] (англ. ''minimum spanning tree, MST'') во взвешенном [[Основные определения теории графов#Неориентированные графы | неориентированном связном графе]]. |
| | | | |
Текущая версия на 19:12, 4 сентября 2022
Алгоритм Прима (англ. Prim's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе.
Идея
Данный алгоритм очень похож на алгоритм Дейкстры. Будем последовательно строить поддерево [math]F[/math] ответа в графе [math]G[/math], поддерживая приоритетную очередь [math]Q[/math] из вершин [math]G \setminus F[/math], в которой ключом для вершины [math]v[/math] является [math]\min\limits_{u \in V(F), uv \in E(G)}w(uv)[/math] — вес минимального ребра из вершин [math]F[/math] в вершины [math]G \setminus F[/math]. Также для каждой вершины в очереди будем хранить [math]p(v)[/math] — вершину [math]u[/math], на которой достигается минимум в определении ключа. Дерево [math]F[/math] поддерживается неявно, и его ребра — это пары [math]\left(v,p(v)\right)[/math], где [math]v \in G \setminus \{r\} \setminus Q[/math], а [math]r[/math] — корень [math]F[/math]. Изначально [math]F[/math] пусто и значения ключей у всех вершин равны [math]+\infty[/math]. Выберём произвольную вершину [math]r[/math] и присвоим её ключу значение [math]0[/math]. На каждом шаге будем извлекать минимальную вершину [math]v[/math] из приоритетной очереди и релаксировать все ребра [math]vu[/math], такие что [math]u \in Q[/math], выполняя при этом операцию [math]\text{decreaseKey}[/math] над очередью и обновление [math]p(v)[/math]. Ребро [math]\left(v,p(v)\right)[/math] при этом добавляется к ответу.
Реализация
// [math]G[/math] — исходный граф
// [math]w[/math] — весовая функция
function [math]\mathtt{primFindMST}():[/math]
for [math]v \in V(G)[/math]
[math]\mathtt{key}[v]\ =\ \infty[/math]
[math]\mathtt{p}[v]\ =[/math] null
[math]r\ =[/math] произвольная вершина графа [math]G[/math]
[math]\mathtt{key}[r]\ =\ \mathtt{0}[/math]
[math]Q.\mathtt{push}(V(G))[/math]
while not [math]Q.\mathtt{isEmpty()}[/math]
[math]v\ =\ Q.\mathtt{extractMin}()[/math]
for [math]vu \in E(G)[/math]
if [math]u \in Q[/math] and [math]\mathtt{key}[u] \gt w(v, u)[/math]
[math]\mathtt{p}[u]\ =\ v[/math]
[math]\mathtt{key}[u]\ =\ w(v, u)[/math]
[math]Q.\mathtt{decreaseKey}(u, \mathtt{key}[u])[/math]
Ребра дерева восстанавливаются из его неявного вида после выполнения алгоритма.
Чтобы упростить операцию [math]\mathrm{decreaseKey}[/math] можно написать кучу на основе сбалансированного бинарного дерева поиска. Тогда просто удалим вершину и добавим ее обратно уже с новым ключом. Асимптотика таких преобразований [math]O(\log n)[/math]. Если же делать с бинарной кучей, то вместо операции [math]\mathrm{decreaseKey}[/math], будем всегда просто добавлять вершину с новым ключом, если из кучи достали вершину с ключом, значение которого больше чем у нее уже стоит, просто игнорировать. Вершин в куче будет не больше [math]n^2[/math], следовательно, операция [math]\mathrm{extractMin}[/math] будет выполняться за [math]O(\log n^2)[/math], что равно [math]O(\log n)[/math]. Максимальное количество вершин, которое мы сможем достать, равняется количеству ребер, то есть [math]m[/math], поэтому общая асимптотика составит [math]O(m \log n)[/math], что хорошо только на разреженных графах.
Пример
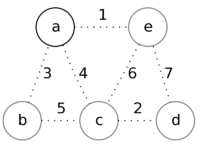
Рассмотрим работу алгоритма на примере графа.
Пусть произвольно выбранная вершина — это вершина a.
| Изображение |
Множество вершин |
Описание
|
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math]\infty[/math] |
[math]\infty[/math] |
[math]\infty[/math] |
[math]\infty[/math]
|
|
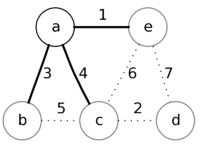
Извлечём из множества вершину a, так как её приоритет минимален.
Рассмотрим смежные с ней вершины b, c, и e.
Обновим их приоритеты, как веса соответствующих рёбер ab, ac и ae, которые будут добавлены в ответ.
|
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math] 3 [/math] |
[math] 4 [/math] |
[math]\infty[/math] |
[math] 1 [/math]
|
|
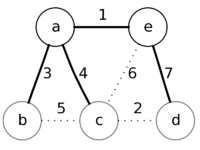
Теперь минимальный приоритет у вершины е.
Извлечём её и рассмотрим смежные с ней вершины a, c, и d.
Изменим приоритет только у вершины d, так как приоритеты вершин a и с меньше,
чем веса у соответствующих рёбер ea и ec, и установим приоритет вершины d равный весу ребра ed, которое будет добавлено в ответ.
|
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math] 3 [/math] |
[math] 4 [/math] |
[math] 7 [/math] |
[math] 1 [/math]
|
|
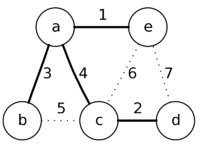
После извлечения вершины b ничего не изменится, так как приоритеты вершин a и с меньше,
чем веса у соответствующих рёбер ba и bc. Однако, после извлечения следующей вершины — c,
будет обновлён приоритет у вершины d на более низкий (равный весу ребра cd) и в ответе ребро ed будет заменено на cd.
|
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math] 3 [/math] |
[math] 4 [/math] |
[math] 2 [/math] |
[math] 1 [/math]
|
|
Далее будет рассмотрена следующая вершина — d, но ничего не изменится,
так как приоритеты вершин e и с меньше, чем веса у соответствующих рёбер de и dc.
После этого алгоритм завершит работу, так как в заданном множестве не останется вершин,
которые не были бы рассмотрены
|
Корректность
По поддерживаемым инвариантам после извлечения вершины [math]v\ (v \neq r)[/math] из [math]Q[/math] ребро [math]\left(v,p(v)\right)[/math] является ребром минимального веса, пересекающим разрез [math]\left(F,Q\right)[/math]. Значит, по лемме о безопасном ребре, оно безопасно. Алгоритм построения MST, добавляющий безопасные ребра, причём делающий это ровно [math]|V|-1[/math] раз, корректен.
Оценка производительности
Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди, как и в алгоритме Дейкстры. Извлечение минимума выполняется [math]V[/math] раз, релаксация — [math]O(E)[/math] раз.
| Структура данных для приоритетной очереди
|
Асимптотика времени работы
|
| Наивная реализация
|
[math]O(V^2+E)[/math]
|
| Двоичная куча
|
[math]O(E\log{V})[/math]
|
| Фибоначчиева куча
|
[math]O(V\log{V}+E)[/math]
|
См. также
Источники информации



