Принадлежность точки выпуклому и невыпуклому многоугольникам — различия между версиями
Yulya3102 (обсуждение | вклад) (→Выпуклый многоугольник) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 5 промежуточных версий 4 участников) | |||
| Строка 12: | Строка 12: | ||
== Невыпуклый многоугольник == | == Невыпуклый многоугольник == | ||
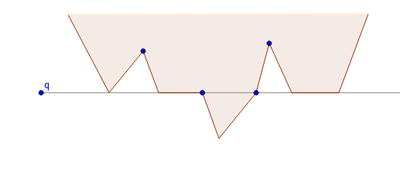
| − | + | [[Файл:Point in polygon.png|400px|thumb|right|Отмечены только те точки, которые являются верхними для какого-либо ребра]] | |
| + | Очевидно, что если пустить из точки луч, то по чётности числа пересечений с рёбрами многоугольника можно определить, внутри точка лежит или снаружи. | ||
| − | + | Пустим луч, например, по иксу, переберём все рёбра и проверим их на пересечение с лучом. | |
| − | + | Луч может попасть в точку, при этом прохождение через точку учтётся два раза (по разу для каждого отрезка, к которым принадлежит точка). Иногда это и есть то, чего нам хочется (когда фигура находится выше или ниже луча), но иногда нам хочется учесть только один раз. Для этого для каждого отрезка учитываем только верхнюю точку. Все случаи попадания луча в точку показаны на рисунке. | |
| − | + | Получившийся алгоритм: | |
| + | |||
| + | * заведём счётчик пересечений и проинициализируем его нулём (либо просто заведём переменную типа bool, показывающую чётность числа пересечений) | ||
| + | * для каждого ребра <tex>ab</tex> многоугольника: | ||
| + | ** если точка запроса <tex>q</tex> лежит на этом ребре, то сразу возвращаем true | ||
| + | ** если <tex>a_y=b_y</tex>, пропускаем этот отрезок, он не влияет на чётность числа пересечений | ||
| + | ** если <tex>q_y=max(a_y, b_y)</tex> и <tex>q_x < min(a_x, b_x)</tex>, увеличим счётчик пересечений | ||
| + | ** если <tex>q_y=min(a_y, b_y)</tex>, пропустим это ребро | ||
| + | ** если <tex>q_y</tex> лежит между <tex>a_y</tex> и <tex>b_y</tex> и поворот точек <tex>a,b,q</tex> левый, то увеличим счётчик пересечений | ||
| + | * если число пересечений чётно, вернём false, иначе вернём true | ||
| + | |||
| + | Время работы алгоритма составляет <tex>O(n)</tex>. | ||
[https://github.com/BorisMinaev/cg/blob/master/include/cg/algo/point_inside_polygon.h Реализация] | [https://github.com/BorisMinaev/cg/blob/master/include/cg/algo/point_inside_polygon.h Реализация] | ||
[[Категория: Вычислительная геометрия]] | [[Категория: Вычислительная геометрия]] | ||
Текущая версия на 19:13, 4 сентября 2022
| Конспект готов к прочтению. |
Выпуклый многоугольник
Выпуклый многоугольник задан как замкнутая полилиния, поэтому для любой вершины этого многоугольника все остальные точки будут отсортированы по углу. Возьмём первую точку многоугольника и мысленно проведём от неё все лучи, содержащие диагонали. Бинпоиском за логарифм можно пройтись по углам и понять, в каком из них лежит точка. Когда найден угол, за константное время можно проверить, с какой стороны от противолежащего первой точке ребра многоугольника лежит точка.
Итоговый алгоритм:
- если искомая точка лежит левее самой левой грани или правее самой правой, сразу возвращаем false
- бинпоиском ищем такое ребро , не инцидентное самой первой точке заданного многоугольника, что повороты точек и различаются
- проверяем поворот точек , если он левый — точка лежит внутри, если правый — снаружи
Итоговое время работы: .
Невыпуклый многоугольник
Очевидно, что если пустить из точки луч, то по чётности числа пересечений с рёбрами многоугольника можно определить, внутри точка лежит или снаружи.
Пустим луч, например, по иксу, переберём все рёбра и проверим их на пересечение с лучом.
Луч может попасть в точку, при этом прохождение через точку учтётся два раза (по разу для каждого отрезка, к которым принадлежит точка). Иногда это и есть то, чего нам хочется (когда фигура находится выше или ниже луча), но иногда нам хочется учесть только один раз. Для этого для каждого отрезка учитываем только верхнюю точку. Все случаи попадания луча в точку показаны на рисунке.
Получившийся алгоритм:
- заведём счётчик пересечений и проинициализируем его нулём (либо просто заведём переменную типа bool, показывающую чётность числа пересечений)
- для каждого ребра многоугольника:
- если точка запроса лежит на этом ребре, то сразу возвращаем true
- если , пропускаем этот отрезок, он не влияет на чётность числа пересечений
- если и , увеличим счётчик пересечений
- если , пропустим это ребро
- если лежит между и и поворот точек левый, то увеличим счётчик пересечений
- если число пересечений чётно, вернём false, иначе вернём true
Время работы алгоритма составляет .