Минимально узкое остовное дерево — различия между версиями
Nemzs (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 13 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Минимально узкое остовное дерево''' (англ. ''Minimum bottleneck spanning tree'', ''MBST'') в связанном взвешенном неориентированном графе <tex>-</tex> | + | __TOC__ |
| − | + | ||
| − | + | {{Определение | |
| − | + | |definition='''Минимально узкое остовное дерево''' (англ. ''Minimum bottleneck spanning tree'', ''MBST'') в связанном взвешенном неориентированном графе <tex>-</tex> [[Остовные деревья: определения, лемма о безопасном ребре|остовное дерево]] графа, у которого максимальное ребро минимально. | |
| − | |||
}} | }} | ||
| − | {{Определение с MBST | + | {{Определение |
| − | | | + | |definition='''Узким ребром''' (англ. ''bottleneck edge'') в графе назовём максимальное по весу. |
| − | |proof=Рассмотрим пример, где MBST не является минимальным остовным деревом: | + | }} |
| + | {{Определение | ||
| + | |definition=Остовное дерево является '''минимально узким''' (англ. ''minimum bottleneck''), если в графе нет остовного дерева с меньшим узким ребром. | ||
| + | }} | ||
| + | == Свойства минимального узкого остовного дерева == | ||
| + | {{Утверждение с MBST | ||
| + | |statement=Каждое минимальное остовное дерево является <tex>\mathrm{MBST}</tex>. | ||
| + | |proof=Предположим, если минимальное остовное не является <tex>\mathrm{MBST}</tex>, значит в графе существует набор ребер которые мы не взяли в наш остов, при замене на которые, наше дерево станет <tex>\mathrm{MBST}</tex>. Также рёбра вне остова должны быть меньше рёбер из остова, чтобы уменьшить минимальное максимально ребро. Но по определению <tex>\mathrm{MST}</tex>, сумма рёбер дерева минимальна, значит вне остова нету рёбер с меньшим весом. Так как наше предположение неверно, <tex>\mathrm{MST}</tex> является <tex>\mathrm{MBST}</tex>. | ||
| + | }} | ||
| + | {{Утверждение с MBST | ||
| + | |statement=<tex>\mathrm{MBST}</tex> не всегда является минимальным остовным деревом. | ||
| + | |proof=Рассмотрим пример, где <tex>\mathrm{MBST}</tex> не является минимальным остовным деревом: | ||
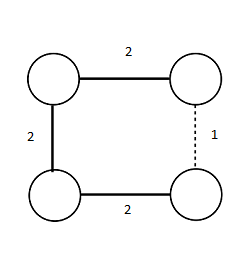
<div class="tleft" style="clear:none">[[Файл:MBST-example.png|left|thumb|700px|Пример MBST дерева.]]</div> | <div class="tleft" style="clear:none">[[Файл:MBST-example.png|left|thumb|700px|Пример MBST дерева.]]</div> | ||
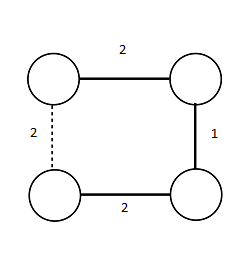
<div class="tleft" style="clear:none">[[Файл:MSTisMBST.png|left|thumb|700px|Пример MST дерева.]]</div> | <div class="tleft" style="clear:none">[[Файл:MSTisMBST.png|left|thumb|700px|Пример MST дерева.]]</div> | ||
}} | }} | ||
| − | == | + | |
| + | == Проверка остовного дерева на узкость == | ||
{{Задача | {{Задача | ||
| − | |definition= | + | |definition=Проверить остовное дерево в графе на <tex>\mathrm{MBST}</tex>. |
}} | }} | ||
=== Алгоритм === | === Алгоритм === | ||
| − | + | Построим новый граф, добавим туда все рёбра меньше максимального из нашего остова. Если в результате у нас получится связный граф, значит мы сможем выделить из него остовное дерево с меньшим узким ребром <tex>-</tex> наше дерево не самое узкое. Иначе, для связности графа нам необходимо добавить максимальные рёбра <tex>-</tex> наше дерево является минимально узким. | |
| + | Найдём максимальное ребро в нашем дереве. Добавим рёбра с весом меньше максимального при помощи [[СНМ (наивные реализации)|СНМ]], чтобы определить его связность. Если в результате у нас все вершины лежат в одном множестве, значит наше дерево не является <tex>\mathrm{MBST}</tex>, иначе оно <tex>\mathrm{MBST}</tex>. | ||
=== Асимптотика === | === Асимптотика === | ||
| − | По каждому ребру пройдём один раз, для поиска максимального, займёт <tex>O(N)</tex>.<br>Работа с СНМ займет <tex>O(N\alpha(V))</tex>, где <tex>\alpha</tex> — обратная функция Аккермана, которая не превосходит <tex>4</tex> во всех практических приложениях и которую можно принять за константу.<br>В результате получаем алгоритм работающий за линейное время <tex>O(N)</tex>. | + | По каждому ребру пройдём один раз, для поиска максимального, займёт <tex>O(N)</tex>, где <tex>N -</tex> число рёбер в графе.<br>Работа с СНМ займет <tex>O(N\alpha(V))</tex>, где <tex>\alpha</tex> — обратная функция Аккермана, которая не превосходит <tex>4</tex> во всех практических приложениях и которую можно принять за константу.<br>В результате получаем алгоритм работающий за линейное время <tex>O(N)</tex>. |
| + | |||
=== Псевдокод === | === Псевдокод === | ||
| + | Все рёбра графа будем хранить в списке <tex>\mathtt{e}</tex>, а рёбра остовного дерева в списке <tex>\mathtt{tree}</tex>.<br> | ||
| + | В каждом ребре <tex>\mathtt{Edge}</tex> храним следующую информацию: | ||
| + | * <tex>\mathtt{from}, \mathtt{to}</tex> {{---}} соединяемые вершины | ||
| + | * <tex>\mathtt{cost}</tex> {{---}} вес ребра | ||
<code> | <code> | ||
| − | ''' | + | '''bool''' ifMBST('''Edge'''[] e, '''Edge'''[] tree): |
| − | '''int''' united = 0 | + | '''int''' united = 0 <font color=green>// Сколько вершин мы объединили</font> |
| − | '''for''' i = 1 to tree.size | + | '''int''' maxEdge = -<tex>\infty</tex> |
| − | maxEdge = max(maxEdge, tree[i].cost) | + | '''for''' i = 1 '''to''' tree.size |
| − | '''for''' i = 1 to n | + | maxEdge = max(maxEdge, tree[i].cost) <font color=green>// Поиск максимального ребра в дереве</font> |
| − | '''if''' e[i].cost >= maxEdge | + | '''for''' i = 1 '''to''' n |
| + | '''if''' e[i].cost >= maxEdge <font color=green>// Не соединяем вершины, если ребро не меньше максимального</font> | ||
'''continue''' | '''continue''' | ||
| − | '''if''' find(e[i].from]) != find(e[i].to) | + | '''if''' find(e[i].from]) != find(e[i].to) <font color=green>// Объединяем вершины, если они в разных множествах</font> |
united++ | united++ | ||
unite(e[i].from,e[i].to) | unite(e[i].from,e[i].to) | ||
| − | '''if''' united == e.size - 1 | + | '''if''' united == e.size - 1 <font color=green>// Дерево подходит, если в результате мы соединили все вершины</font> |
| − | '''return''' true | + | '''return''' ''true'' |
'''else''' | '''else''' | ||
| − | '''return''' false | + | '''return''' ''false'' |
</code> | </code> | ||
| + | |||
==Cм. также== | ==Cм. также== | ||
*[[Алгоритм Краскала]] | *[[Алгоритм Краскала]] | ||
Текущая версия на 19:13, 4 сентября 2022
Содержание
| Определение: |
| Минимально узкое остовное дерево (англ. Minimum bottleneck spanning tree, MBST) в связанном взвешенном неориентированном графе остовное дерево графа, у которого максимальное ребро минимально. |
| Определение: |
| Узким ребром (англ. bottleneck edge) в графе назовём максимальное по весу. |
| Определение: |
| Остовное дерево является минимально узким (англ. minimum bottleneck), если в графе нет остовного дерева с меньшим узким ребром. |
Свойства минимального узкого остовного дерева
| Утверждение c MBST: |
Каждое минимальное остовное дерево является . |
| Предположим, если минимальное остовное не является , значит в графе существует набор ребер которые мы не взяли в наш остов, при замене на которые, наше дерево станет . Также рёбра вне остова должны быть меньше рёбер из остова, чтобы уменьшить минимальное максимально ребро. Но по определению , сумма рёбер дерева минимальна, значит вне остова нету рёбер с меньшим весом. Так как наше предположение неверно, является . |
| Утверждение c MBST: |
не всегда является минимальным остовным деревом. |
|
Рассмотрим пример, где не является минимальным остовным деревом: |
Проверка остовного дерева на узкость
| Задача: |
| Проверить остовное дерево в графе на . |
Алгоритм
Построим новый граф, добавим туда все рёбра меньше максимального из нашего остова. Если в результате у нас получится связный граф, значит мы сможем выделить из него остовное дерево с меньшим узким ребром наше дерево не самое узкое. Иначе, для связности графа нам необходимо добавить максимальные рёбра наше дерево является минимально узким. Найдём максимальное ребро в нашем дереве. Добавим рёбра с весом меньше максимального при помощи СНМ, чтобы определить его связность. Если в результате у нас все вершины лежат в одном множестве, значит наше дерево не является , иначе оно .
Асимптотика
По каждому ребру пройдём один раз, для поиска максимального, займёт , где число рёбер в графе.
Работа с СНМ займет , где — обратная функция Аккермана, которая не превосходит во всех практических приложениях и которую можно принять за константу.
В результате получаем алгоритм работающий за линейное время .
Псевдокод
Все рёбра графа будем хранить в списке , а рёбра остовного дерева в списке .
В каждом ребре храним следующую информацию:
- — соединяемые вершины
- — вес ребра
bool ifMBST(Edge[] e, Edge[] tree):
int united = 0 // Сколько вершин мы объединили
int maxEdge = -
for i = 1 to tree.size
maxEdge = max(maxEdge, tree[i].cost) // Поиск максимального ребра в дереве
for i = 1 to n
if e[i].cost >= maxEdge // Не соединяем вершины, если ребро не меньше максимального
continue
if find(e[i].from]) != find(e[i].to) // Объединяем вершины, если они в разных множествах
united++
unite(e[i].from,e[i].to)
if united == e.size - 1 // Дерево подходит, если в результате мы соединили все вершины
return true
else
return false