Цели и средства нормализации — различия между версиями
м (→Теорема Хита) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 20 промежуточных версий 2 участников) | |||
| Строка 4: | Строка 4: | ||
'''Нормализация''' — процесс преобразования отношений реляционной базы данных к виду, отвечающему одной из нормальных форм. | '''Нормализация''' — процесс преобразования отношений реляционной базы данных к виду, отвечающему одной из нормальных форм. | ||
}} | }} | ||
| − | + | Нормализация помогает привести базу данных к виду обеспечивающему минимальную логическую избыточность. Эта цель достигается благодаря тому, что в полностью нормализованном проекте предикаты переменных отношения имеют более простой вид. | |
__TOC__ | __TOC__ | ||
===Цели=== | ===Цели=== | ||
| Строка 13: | Строка 13: | ||
===Следствия=== | ===Следствия=== | ||
| − | Полная нормализация приводит к | + | Полная нормализация приводит к увеличению количества логически независимых переменных отношения, что может привести к снижению скорости выборки ⇒ к замедлению работы базы данных. |
==Средства нормализации== | ==Средства нормализации== | ||
| + | Для приведения базы данных в нормальную форму будет применяться декомпозиция без потерь. При построении такой декомпозиции используются операции соединения и проекции. | ||
===Проекция=== | ===Проекция=== | ||
{{Определение | {{Определение | ||
| Строка 22: | Строка 23: | ||
'''Проекция''' отношения <tex>R</tex> на множество атрибутов <tex>X</tex>: <tex>\pi_X(R) =\{r \cap X|r\in R\}</tex> — это отношение удовлетворяющее свойствам: | '''Проекция''' отношения <tex>R</tex> на множество атрибутов <tex>X</tex>: <tex>\pi_X(R) =\{r \cap X|r\in R\}</tex> — это отношение удовлетворяющее свойствам: | ||
* Его заголовок формируется из заголовка отношения <tex>R</tex> путем удаления всех атрибутов, не указанных в множестве <tex>X</tex> | * Его заголовок формируется из заголовка отношения <tex>R</tex> путем удаления всех атрибутов, не указанных в множестве <tex>X</tex> | ||
| − | * Тело состоит из всех кортежей <tex>{Х_1 r_1 , X_2 r_2, . . . , X_n r_n }</tex>, таких что в отношении <tex>R</tex> присутствует кортеж со значением <tex>r_1</tex> атрибута <tex>X_1</tex>, <tex>r_2</tex> атрибута <tex>X_2</tex> и т.д. | + | * Тело состоит из всех кортежей <tex>{Х_1:r_1 , X_2:r_2, . . . , X_n:r_n }</tex>, таких что в отношении <tex>R</tex> присутствует кортеж со значением <tex>r_1</tex> атрибута <tex>X_1</tex>, <tex>r_2</tex> атрибута <tex>X_2</tex> и т.д. |
}} | }} | ||
| Строка 32: | Строка 33: | ||
|id = natural join | |id = natural join | ||
|definition = | |definition = | ||
| − | '''Естественное соединение''' (англ. ''natural join'') отношений <tex> | + | '''Естественное соединение''' (англ. ''natural join'') отношений <tex>R_1</tex> и <tex>R_2</tex>: <tex>R_1 ⋈ R_2 = \{r_1 ∪ r_2 | r_1 ∈ R_1, r_2 ∈ R_2 ∧ π_Y(r_1) = π_Y(r_2)\}</tex> — отношение с заголовком <tex>\{X, Y, Z\}</tex> и телом, состоящим из всех таких кортежей <tex>\{Х_i:х_i</tex>, <tex>Y_j:y_j</tex>, . . . , <tex>Z_k:z_k\}</tex>, что любой из этих кортежей присутствует и в отношении <tex>R_1</tex>, со значением <tex>x_i</tex> атрибута <tex>Х_i</tex> и значением <tex>y_j</tex> атрибута <tex>Y_j</tex>, и в отношении <tex>R_2</tex>, со значением <tex>y_i</tex> атрибута <tex>Y_i</tex> и значением <tex>z_k</tex> атрибута <tex>Z_k</tex>. |
}} | }} | ||
* Можно понимать как соединение по совпадающим атрибутам | * Можно понимать как соединение по совпадающим атрибутам | ||
| − | * Коммутативно: <tex> | + | * Коммутативно: <tex>R_1 ⋈ R_2 = R_2 ⋈ R_1</tex> |
| − | * Ассоциативно: <tex>( | + | * Ассоциативно: <tex>(R_1 ⋈ R_2) ⋈ R_3 = R_1 ⋈ (R_2 ⋈ R_3)</tex> |
[[Файл:Join.png]] | [[Файл:Join.png]] | ||
| Строка 57: | Строка 58: | ||
====Пример некорректной декомпозиции==== | ====Пример некорректной декомпозиции==== | ||
| + | При обратном соединении полученных отношений исходное отношений не было восстановлено — появились записи, которых не было ⇒ декомпозиция некорректна. | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Строка 93: | Строка 95: | ||
Поскольку <tex>X → Y</tex>, существует единственный <tex>y: (x, y) ∈ π_{XY}(R) ⇒ y = y' ⇒ (x, y, z) ∈ R</tex> | Поскольку <tex>X → Y</tex>, существует единственный <tex>y: (x, y) ∈ π_{XY}(R) ⇒ y = y' ⇒ (x, y, z) ∈ R</tex> | ||
}} | }} | ||
| + | |||
| + | Доказательсто первого пункта не опирается на наличие функциональной зависимости ⇒ справедливо следствие: | ||
| + | |||
| + | '''Следствие''' Исходное отношение <tex>R</tex> всегда является подмножеством соединения отношений, полученных при декомпозиции. | ||
==См. также== | ==См. также== | ||
Текущая версия на 19:13, 4 сентября 2022
| Определение: |
| Нормализация — процесс преобразования отношений реляционной базы данных к виду, отвечающему одной из нормальных форм. |
Нормализация помогает привести базу данных к виду обеспечивающему минимальную логическую избыточность. Эта цель достигается благодаря тому, что в полностью нормализованном проекте предикаты переменных отношения имеют более простой вид.
Содержание
Цели
- Исключение некоторых типов избыточности
- Устранение аномалий
- Разработка проекта базы данных, который является достаточно «качественным» представлением реального мира, интуитивно понятен и может служить хорошей основой для последующего расширения
- Упрощение процедуры применения необходимых ограничений целостности
Следствия
Полная нормализация приводит к увеличению количества логически независимых переменных отношения, что может привести к снижению скорости выборки ⇒ к замедлению работы базы данных.
Средства нормализации
Для приведения базы данных в нормальную форму будет применяться декомпозиция без потерь. При построении такой декомпозиции используются операции соединения и проекции.
Проекция
| Определение: |
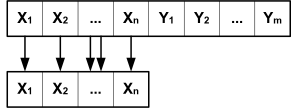
Проекция отношения на множество атрибутов : — это отношение удовлетворяющее свойствам:
|
Соединение
Операция соединения имеет несколько разных вариантов, но чаще всего рассматривается естественное соединение.
| Определение: |
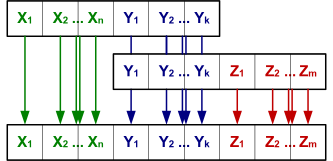
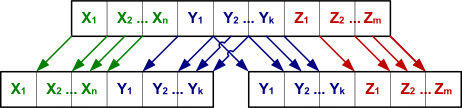
| Естественное соединение (англ. natural join) отношений и : — отношение с заголовком и телом, состоящим из всех таких кортежей , , . . . , , что любой из этих кортежей присутствует и в отношении , со значением атрибута и значением атрибута , и в отношении , со значением атрибута и значением атрибута . |
- Можно понимать как соединение по совпадающим атрибутам
- Коммутативно:
- Ассоциативно:
Декомпозиция
Процедура нормализации предусматривает разбиение, или декомпозицию, данной переменной отношения на другие переменные отношения, причем декомпозиция должна быть обратимой, т.е. выполняться без потерь информации, то есть, соединение отношений, полученных при декомпозиции множества, должно давать исходное отношение Декомпозиция отношения на множества атрибутов и :
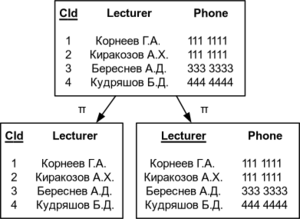
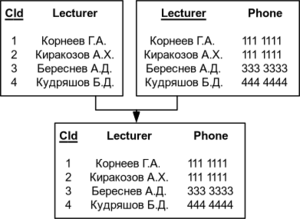
Пример корректной декомпозиции
| Проекции на CId Phone и Lecturer Phone | Соединение CId Lecturer и Lecturer Phone |
|
|
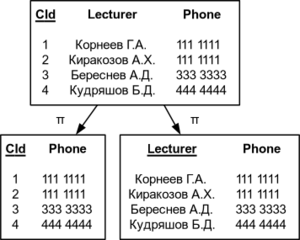
Пример некорректной декомпозиции
При обратном соединении полученных отношений исходное отношений не было восстановлено — появились записи, которых не было ⇒ декомпозиция некорректна.
| Проекции на CId Phone и Lecturer Phone | Соединение CId Phone и Lecturer Phone |
|

|
Теорема Хита
Теорема Хита утверждает, что если некоторая декомпозиция выполняется в соответствии с определенной функциональной зависимостью, то она будет выполнена без потерь.
| Теорема (Хит): |
Пусть является отношением, где , и — неперескающиеся множества атрибутов. Если удовлетворяет функциональной зависимости , то равно соединению его проекций по атрибутам , и , : |
| Доказательство: |
|
Докажем равенство в обе стороны: 1. Докажем, что исходное отношение — подмножество соединения проекций. Рассмотрим произвольный кортеж из отношения . Для проекций кортежа на и выполняетя: . Из этого следует, что — подмножество соединения проекций ⋈. 2. Докажем, что любой кортеж полученного соединения является кортежем отношения . Рассмотрим кортеж , принадлежащий соединению Для того, чтобы был в соеденении, необходимо, чтобы существовали кортежи и Из следует, что существует кортеж для некоторого . Это означает, что должен существовать кортеж Поскольку , существует единственный |
Доказательсто первого пункта не опирается на наличие функциональной зависимости ⇒ справедливо следствие:
Следствие Исходное отношение всегда является подмножеством соединения отношений, полученных при декомпозиции.
См. также
- Функциональные зависимости: замыкание, эквивалентность и правила вывода
- Нормальные формы: первая и вторая
- Нормальные формы: третья и Бойса-Кодда
- Многозначные зависимости и четвертая нормальная форма
- Зависимости соединения и пятая нормальная форма
Источники информации
- kgeorgiy.info Тема 4. Нормализация баз данных
- Дейт К.: Введение в системы баз данных (Глава 12)