Теорема Турана об экстремальном графе — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 10 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
==Теорема Турана== | ==Теорема Турана== | ||
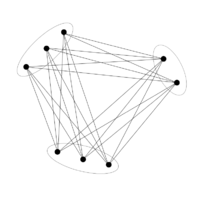
[[Файл:Turan example.png|200px|thumb|right|Пример графа Турана при <tex>n = 8, r = 4</tex>]] | [[Файл:Turan example.png|200px|thumb|right|Пример графа Турана при <tex>n = 8, r = 4</tex>]] | ||
| − | '''Теорема Ту́рана''' (англ. ''Turán's theorem'') {{---}} классическая теорема экстремальной теории графов. | + | '''Теорема Ту́рана''' (англ. ''Turán's theorem'') {{---}} классическая теорема экстремальной теории графов<ref>[https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D1%81%D1%82%D1%80%D0%B5%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2 Экстремальная теория графов]</ref>. |
| − | Она послужила образцом для большого количества подобных теорем, которые изучают некоторые глобальные параметры | + | Она послужила образцом для большого количества подобных теорем, которые изучают, как наличие тех или иных подструктур влияет на некоторые глобальные параметры ([[Раскраска графа|хроматическое число]]). |
| − | Впервые | + | Впервые теорему сформулировал венгерский математик Пал Туран в <tex>1941</tex> году. |
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | <tex> | + | <tex>K_n</tex> {{---}} полный граф на <tex>n</tex> вершинах. |
}} | }} | ||
| + | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | + | <tex>ex(n, K_r)</tex> {{---}} максимальное количество ребер, которое может иметь граф на <tex>n</tex> вершинах, не включая в себя <tex>K_r</tex> как подграф. | |
}} | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Граф Турана''' <tex>T^{r-1}(n)</tex> {{---}} полный <tex>(r - 1)</tex>-[[Двудольные графы|дольный]] граф на <tex>n > r-1</tex> вершинах, доли которого по мощности отличаются не более чем на <tex>1</tex>. Если количество вершин не превосходит количество долей (<tex>n \leqslant r - 1</tex>), то <tex>T^{r-1}(n) = K_n</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | <tex>t_{r-1}(n)</tex> {{---}} количество ребер в <tex>T^{r-1}(n)</tex>. | ||
| + | }} | ||
| + | |||
{{Лемма | {{Лемма | ||
| Строка 19: | Строка 31: | ||
Если <tex>G</tex> {{---}} <tex>(r - 1)</tex>-дольный граф с максимальным количеством ребер, то <tex>G = T^{r-1}(n)</tex>. | Если <tex>G</tex> {{---}} <tex>(r - 1)</tex>-дольный граф с максимальным количеством ребер, то <tex>G = T^{r-1}(n)</tex>. | ||
|proof= | |proof= | ||
| − | Докажем от противного. Пусть существует <tex>(r - 1)</tex>-дольный граф с максимальным числом ребер, который не | + | Докажем от противного. Пусть существует <tex>(r - 1)</tex>-дольный граф с максимальным числом ребер, который не является графом Турана. |
Обозначим его <tex>G_m</tex>. | Обозначим его <tex>G_m</tex>. | ||
Очевидно, что <tex>G_m</tex> является полным <tex>(r - 1)</tex>-дольным. | Очевидно, что <tex>G_m</tex> является полным <tex>(r - 1)</tex>-дольным. | ||
Так как <tex>G_m \ne T^{r-1}(n) </tex>, то в <tex>G_m</tex> существуют доли <tex>V_1</tex> и <tex>V_2</tex>, что <tex>|V_1| - |V_2| > 1</tex>. | Так как <tex>G_m \ne T^{r-1}(n) </tex>, то в <tex>G_m</tex> существуют доли <tex>V_1</tex> и <tex>V_2</tex>, что <tex>|V_1| - |V_2| > 1</tex>. | ||
| − | Но тогда | + | Но тогда возьмем вершину <tex>a \in V_1</tex> и перекинем ее в <tex>V_2</tex>. Тогда количество вершин, которые не могут быть соседями <tex>a</tex> уменьшилось с размером ее доли. Остальной граф не изменился, поэтому общее количество ребер увеличилось. |
| − | Это противоречит предположению, что граф <tex>G_m</tex> максимален по числу ребер. | + | Это противоречит предположению, что граф <tex>G_m</tex> максимален по числу ребер. |
| + | |||
| + | Значит лемма доказана. | ||
}} | }} | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Для всех | + | Для всех натуральных чисел <tex>r</tex>, <tex>n</tex>, где <tex>r > 1</tex>, любой граф <tex>G \nsubseteq K_r</tex> с <tex>n</tex> вершинами и <tex>ex(n, K_r)</tex> ребрами есть <tex>T^{r-1}(n)</tex>. |
|proof= | |proof= | ||
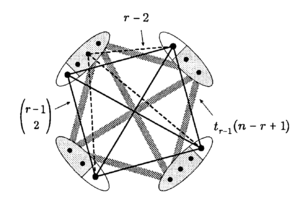
[[Файл:Turan theorem induction step.png|300px|thumb|left|Шаг индукции]] | [[Файл:Turan theorem induction step.png|300px|thumb|left|Шаг индукции]] | ||
| Строка 35: | Строка 49: | ||
'''База:''' | '''База:''' | ||
| − | При <tex>n \leqslant r - 1</tex> имеем <tex>G = | + | При <tex>n \leqslant r - 1</tex> имеем <tex>G = K_n = T^{r-1}(n)</tex>, что и утверждалось. База доказана. |
'''Шаг индукции:''' | '''Шаг индукции:''' | ||
Пусть теперь <tex>n \geqslant r</tex>. | Пусть теперь <tex>n \geqslant r</tex>. | ||
| − | Поскольку <tex>G</tex> реберно-максимален и не содержит подграфа <tex> | + | Поскольку <tex>G</tex> реберно-максимален и не содержит подграфа <tex>K_r</tex>, то <tex>G</tex> содержит подграф <tex>K^{r-1}</tex>. |
| − | Обозначим любой из них как <tex>K</tex>. | + | Обозначим любой из них как <tex>K</tex>. |
| − | Тогда по индукционному предположению <tex>G - K</tex> имеет не более <tex>t_{r-1}(n - r + 1)</tex> ребер, а любая вершина <tex>G - K</tex> имеет не более <tex>r - 2</tex> соседей в <tex>K.</tex> | + | Тогда по индукционному предположению <tex>G - K</tex> имеет не более <tex>t_{r-1}(n - r + 1)</tex> ребер, а любая вершина <tex>G - K</tex> имеет не более <tex>r - 2</tex> соседей в <tex>K.</tex> |
Следовательно мы можем оценить количество ребер в <tex>G</tex>: | Следовательно мы можем оценить количество ребер в <tex>G</tex>: | ||
| − | <tex>|E(G)| \leqslant \underbrace{t_{r-1}(n + | + | <tex>|E(G)| \leqslant \underbrace{t_{r-1}(n - r + 1)}_{G-K} + \underbrace{(n - r + 1)(r - 2)}_{(G-K) \rightleftarrows (K)} + \underbrace{{r-1 \choose 2}}_{K} = t_{r-1}(n); (1)</tex> |
Равенство справа следует непосредственно из графа Турана <tex>T^{r-1}(n)</tex>. | Равенство справа следует непосредственно из графа Турана <tex>T^{r-1}(n)</tex>. | ||
| − | Поскольку <tex>G</tex> экстремален для <tex> | + | Поскольку <tex>G</tex> экстремален для <tex>K_r</tex>, то в <tex>(1)</tex> имеет место равенство. |
Таким образом, любая вершина из <tex>G - K</tex> имеет ровно <tex>r - 2</tex> соседа в <tex>K</tex> {{---}} точно так же, как и вершины <tex>x_1,\cdots, x_{r-1}</tex> из самого <tex>K</tex>. | Таким образом, любая вершина из <tex>G - K</tex> имеет ровно <tex>r - 2</tex> соседа в <tex>K</tex> {{---}} точно так же, как и вершины <tex>x_1,\cdots, x_{r-1}</tex> из самого <tex>K</tex>. | ||
| − | При <tex>i = 1,\cdots, r-1</tex> пусть <tex>V_i | + | При <tex>i = 1,\cdots, r-1</tex> пусть <tex>V_i = \{v \in V(G) \mid vx_i \not\in E(G)\}</tex> есть множество всех вершин <tex>G</tex>, чьи <tex>r - 2</tex> соседей в <tex>K</tex> отличны от <tex>x_i</tex>. |
| − | Так как каждая вершина <tex>G - K</tex> имеет ровно <tex>r - 2</tex> соседа в <tex>K</tex>, то все <tex>V_i</tex> не зависимы. | + | Так как каждая вершина <tex>G - K</tex> имеет ровно <tex>r - 2</tex> соседа в <tex>K</tex>, то все <tex>V_i</tex> не зависимы. |
| − | При этом они в объединении дают <tex>V(G)</tex> поскольку <tex> | + | При этом они в объединении дают <tex>V(G)</tex> поскольку <tex>K_r \nsubseteq G</tex>. |
Следовательно, граф <tex>G</tex> является <tex>(r-1)</tex>-дольным. | Следовательно, граф <tex>G</tex> является <tex>(r-1)</tex>-дольным. | ||
| − | + | Тогда по лемме из предположения об экстремальности <tex>G</tex> следует, что <tex>G = T^{r-1}(n)</tex>. | |
}} | }} | ||
| + | |||
==См. также== | ==См. также== | ||
*[[Раскраска графа]] | *[[Раскраска графа]] | ||
*[[Двудольные графы]] | *[[Двудольные графы]] | ||
| + | ==Примечания== | ||
| + | <references /> | ||
==Источники информации== | ==Источники информации== | ||
| − | ''Дистель, Рейнград.'' Теория графов: Пер. с англ. — Новосибирск: Изд-во Ин-та математики, 2002. — 166-170 стр. — ISBN 5-86134-101-X. | + | *''Дистель, Рейнград.'' Теория графов: Пер. с англ. — Новосибирск: Изд-во Ин-та математики, 2002. — 166-170 стр. — ISBN 5-86134-101-X. |
| + | *[https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D1%81%D1%82%D1%80%D0%B5%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B3%D1%80%D0%B0%D1%84%D0%BE%D0%B2 Экстремальная теория графов] | ||
| + | |||
| + | [[Категория: Раскраски графов]] | ||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
Текущая версия на 19:15, 4 сентября 2022
Теорема Турана
Теорема Ту́рана (англ. Turán's theorem) — классическая теорема экстремальной теории графов[1]. Она послужила образцом для большого количества подобных теорем, которые изучают, как наличие тех или иных подструктур влияет на некоторые глобальные параметры (хроматическое число).
Впервые теорему сформулировал венгерский математик Пал Туран в году.
| Определение: |
| — полный граф на вершинах. |
| Определение: |
| — максимальное количество ребер, которое может иметь граф на вершинах, не включая в себя как подграф. |
| Определение: |
| Граф Турана — полный -дольный граф на вершинах, доли которого по мощности отличаются не более чем на . Если количество вершин не превосходит количество долей (), то . |
| Определение: |
| — количество ребер в . |
| Лемма: |
Если — -дольный граф с максимальным количеством ребер, то . |
| Доказательство: |
|
Докажем от противного. Пусть существует -дольный граф с максимальным числом ребер, который не является графом Турана. Обозначим его . Очевидно, что является полным -дольным. Так как , то в существуют доли и , что . Но тогда возьмем вершину и перекинем ее в . Тогда количество вершин, которые не могут быть соседями уменьшилось с размером ее доли. Остальной граф не изменился, поэтому общее количество ребер увеличилось. Это противоречит предположению, что граф максимален по числу ребер. Значит лемма доказана. |
| Теорема: |
Для всех натуральных чисел , , где , любой граф с вершинами и ребрами есть . |
| Доказательство: |
|
Применим индукцию по . База: При имеем , что и утверждалось. База доказана. Шаг индукции: Пусть теперь . Поскольку реберно-максимален и не содержит подграфа , то содержит подграф . Обозначим любой из них как . Тогда по индукционному предположению имеет не более ребер, а любая вершина имеет не более соседей в Следовательно мы можем оценить количество ребер в :
Равенство справа следует непосредственно из графа Турана . Поскольку экстремален для , то в имеет место равенство. Таким образом, любая вершина из имеет ровно соседа в — точно так же, как и вершины из самого . При пусть есть множество всех вершин , чьи соседей в отличны от . Так как каждая вершина имеет ровно соседа в , то все не зависимы. При этом они в объединении дают поскольку . Следовательно, граф является -дольным. Тогда по лемме из предположения об экстремальности следует, что . |
См. также
Примечания
Источники информации
- Дистель, Рейнград. Теория графов: Пер. с англ. — Новосибирск: Изд-во Ин-та математики, 2002. — 166-170 стр. — ISBN 5-86134-101-X.
- Экстремальная теория графов