Марковская цепь — различия между версиями
Vsklamm (обсуждение | вклад) (→Циклический класс) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 8 промежуточных версий 2 участников) | |||
| Строка 94: | Строка 94: | ||
}} | }} | ||
| − | Если цепь циклическая, у неё есть некоторый период <tex> d > 1 </tex>, а её состояния подразделяются на <tex> d </tex> циклических | + | Если цепь циклическая, у неё есть некоторый период <tex> d > 1 </tex>, а её состояния подразделяются на <tex> d </tex> циклических классов. Цепь движется по циклическим классам в определённом порядке, возвращаясь в класс с начальным состоянием через <tex> d </tex> шагов. |
Топология циклических цепей разнообразна. Самым тривиальным случаем является элементарный цикл из <tex> n </tex> состояний и, следовательно, содержащий <tex> n </tex> циклический классов. Более сложный случай – простые циклы. Простой цикл состоит из | Топология циклических цепей разнообразна. Самым тривиальным случаем является элементарный цикл из <tex> n </tex> состояний и, следовательно, содержащий <tex> n </tex> циклический классов. Более сложный случай – простые циклы. Простой цикл состоит из | ||
нескольких циклов, пересекающихся по вершинам, но не пересекающихся по | нескольких циклов, пересекающихся по вершинам, но не пересекающихся по | ||
ребрам. Все эти циклы обязаны не быть взаимно простыми. Иначе НОД длин | ребрам. Все эти циклы обязаны не быть взаимно простыми. Иначе НОД длин | ||
| − | этих циклов равен единице, и | + | этих циклов равен единице, и цепь регулярна. Общий случай циклической цепи – цепь, состоящая из циклов, пересекающихся по вершинам и ребрам в представлении цепи как графа. |
| + | |||
| + | ==== Примеры циклических цепей ==== | ||
| + | |||
| + | {| class = "wikitable" | ||
| + | ! Изображение !! Матрица переходов !! Описание | ||
| + | |- | ||
| + | |style="background-color:#FFF" |[[Файл:N steps chain.png|400px|center|Элементарный цикл]] | ||
| + | |<tex>\begin{pmatrix} | ||
| + | 0 & 1 & 0 & \cdots & 0 & 0 & 0 \\ | ||
| + | 0 & 0 & 1 & \cdots & 0 & 0 & 0 \\ | ||
| + | \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ | ||
| + | 0 & 0 & 0 & \cdots & 0 & 0 & 1 \\ | ||
| + | 1 & 0 & 0 & \cdots & 0 & 0 & 0 | ||
| + | \end{pmatrix}_N | ||
| + | </tex> | ||
| + | | Стохастическая матрица элементарного цикла всегда имеет по одной единице в каждом столбце и каждой строке. Таким образом, нужно ровно <tex> n </tex> шагов, проходящих через все вершины, чтобы попасть из вершины <tex> j </tex> в неё же. | ||
| + | |- | ||
| + | |style="background-color:#FFF" |[[Файл:Prime cyclic chain.png|200px|center|Простой цикл]] | ||
| + | |<tex>\begin{pmatrix} | ||
| + | 0 & 0 & 0,5 & 0,5 & 0 & 0 \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 \\ | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 1 \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{pmatrix} | ||
| + | </tex> | ||
| + | |Этот простой цикл состоит из двух элементарных, пересекающихся в вершине <tex> 1 </tex>. НОД длин всех путей из вершины <tex> 1 </tex> в вершину <tex> 1 </tex> равен <tex> 1 </tex>, поэтому можно получить предельное распределение. | ||
| + | |- | ||
| + | |} | ||
=== Поглощающая цепь === | === Поглощающая цепь === | ||
Текущая версия на 19:17, 4 сентября 2022
| Определение: |
| Цепь Маркова (англ. Markov chain) — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем, что при фиксированном настоящем будущее независимо от прошлого.
Процесс в каждый момент времени находится в одном из состояний. При этом, если он находится в состоянии с номером , то он перейдет в состояние с вероятностью . Матрицу называют матрицей переходов (англ. transition matrix). |
На матрицу переходов накладываются следующие условия:
Такая матрица называется стохастической.
Марковскую цепь можно представить в виде графа, в котором вершины — это состояния процесса, а ребра — переходы между состояниями, и на ребре из в написана вероятность перехода из в , то есть .
Содержание
Распределение вероятностей
Марковскую цепь в любой момент времени можно охарактеризовать вектором-строкой — распределением вероятностей по состояниям цепи ( — вероятность цепи в момент времени быть в состоянии ).
Если — текущее распределение вероятностей, то можно узнать распределение на следующем шаге, умножив вектор на матрицу перехода:
.
Из ассоциативности произведения матриц следует, что для того, чтобы узнать распределение вероятностей через шагов, нужно умножить на матрицу перехода, возведённую в степень :
.
Для марковской цепи иногда задают начальное распределение , хотя во многих классах марковских цепей распределение по прошествии большого периода времени от него не зависит (такое распределение называют предельным (англ. limiting distribution)).
Достижимость и сообщаемость
Обозначим вероятность попасть из состояния в состояние за переходов как .
| Определение: |
| Состояние достижимо (англ. accesible) из состояния , если существует такое , что . Достижимость из обозначается . |
| Определение: |
| Состояния и сообщаются (англ. communicate), если они достижимы друг из друга. Сообщаемость и обозначается . |
Классификация цепей и состояний
Неразложимая цепь
| Определение: |
| Неразложимый класс (англ. communicating class) — класс эквивалентности множества состояний по отношению сообщаемости. Если представить марковскую цепь как граф, неразложимый класс будет аналогичен компоненте сильной связности. |
| Определение: |
| Неразложимая цепь (англ. irreducible chain) — цепь Маркова, в которой все состояния образуют один неразложимый класс. |
Эргодическая цепь
| Определение: |
| Упорядочим (очевидно, упорядочение будет частичным) неразложимые классы отношением достижимости. Минимальные элементы в таком упорядочении называются эргодическими классами (англ. ergodic classes). Состояния в эргодических классах называются эргодическими (англ. ergodic), возвратными, или существенными (англ. essential). Все остальные неразложимые классы называются невозвратными классами. Состояния, входящие в них, называются невозвратными или несущественными (англ. inessential). |
Если эргодический класс состоит из одного состояния, такое состояние является поглощающим. Из свойств частичного упорядочения, в любой цепи Маркова найдется хотя бы один эргодический класс.
| Определение: |
| Эргодическая марковская цепь (англ. ergodic Markov chain) — марковская цепь, целиком состоящая из одного эргодического класса. |
Пусть — множество таких , что находясь в состоянии , можно оказаться в состоянии через шагов. — наибольший общий делитель чисел из множества .
| Лемма: |
Для и , принадлежащих одному классу эквивалентности по отношению достижимости, и числа из множества сравнимы между собой по модулю . |
| Доказательство: |
| Пусть . Из можно попасть в и обратно, значит, . Также после попадания в можно сколько угодно раз перейти из него в самого себя, и только потом перейти в , для этого понадобится шагов при любом достаточно большом . Значит, должно делиться на . Но аналогично можно доказать, что делится на , поэтому . Также можно перейти за шагов в , а потом попасть в , поэтому . Значит, и оба делятся на , то есть и сравнимы между собой по модулю . |
Введём числа , так, что любой элемент из сравним с по модулю .
Циклический класс
| Определение: |
| Циклический класс (англ. cyclic class) — класс, для любых элементов и которого верно равенство . |
| Определение: |
| Если цепь состоит целиком из одного циклического класса, её называют регулярной, иначе — циклической. |
Если цепь циклическая, у неё есть некоторый период , а её состояния подразделяются на циклических классов. Цепь движется по циклическим классам в определённом порядке, возвращаясь в класс с начальным состоянием через шагов.
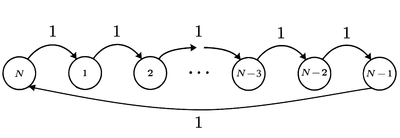
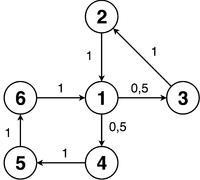
Топология циклических цепей разнообразна. Самым тривиальным случаем является элементарный цикл из состояний и, следовательно, содержащий циклический классов. Более сложный случай – простые циклы. Простой цикл состоит из нескольких циклов, пересекающихся по вершинам, но не пересекающихся по ребрам. Все эти циклы обязаны не быть взаимно простыми. Иначе НОД длин этих циклов равен единице, и цепь регулярна. Общий случай циклической цепи – цепь, состоящая из циклов, пересекающихся по вершинам и ребрам в представлении цепи как графа.
Примеры циклических цепей
| Изображение | Матрица переходов | Описание |
|---|---|---|
| Стохастическая матрица элементарного цикла всегда имеет по одной единице в каждом столбце и каждой строке. Таким образом, нужно ровно шагов, проходящих через все вершины, чтобы попасть из вершины в неё же. | ||
| Этот простой цикл состоит из двух элементарных, пересекающихся в вершине . НОД длин всех путей из вершины в вершину равен , поэтому можно получить предельное распределение. |
Поглощающая цепь
| Определение: |
| Поглощающее состояние (англ. absorbing state) — состояние, из которого нельзя попасть ни в какое другое, то есть — поглощающее состояние, если . |
| Определение: |
| Поглощающей (англ. absorbing chain) называется марковская цепь, в которой есть хотя бы одно поглощающее состояние и из любого состояния достижимо хотя бы одно поглощающее. |
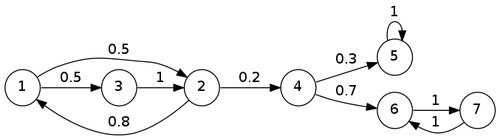
В примере на рисунке поглощающими являются состояния и , а непоглощающими — и .
Пример
На рисунке:
- достижимыми состояниями являются: из (непосредственно), из (непосредственно), из (к примеру, через цепочку состояний ) и т.д.
- сообщаются состояния и (непосредственно), и (непосредственно), и (достижимы друг из друга) и т. д.
- неразложимыми классами являются множества вершин , , , ;
- эргодическими классами являются множества вершин , ;
- поглощающим состоянием является состояние .
- если расматривать отдельно, можно выделить два циклических класса и (на каждом шаге цепь переходит из одного состояния в другое, а через шага возвращается в одно и то же состояние.
Подсчет количества поглощащих состояний
Пусть — массив переходов марковской цепи, где — вероятность перехода из состояния в . Тогда, по определению поглощающего состояния, если — поглощающее состояние, то . По этому признаку помно определить все поглощающие состояния в цепи.
Псевдокод
- — массив состояний. Если — посглощающее состояние, то
- — количество состояний
- — количество переходов
function findAbsorbings(transition: int[m][2]):
boolean absorbing[m]
for i = 0 to m - 1
if transition[i][0] == transition[i][1] and transition[i][2] == 1
absorbing[transition[i][0]] = true
return absorbing
См. также
Источники информации
- Романовский И. В. Дискретный анализ. — СПб.: Невский Диалект; БХВ-Петербург, 2003. — С. 270—279. — ISBN 5-7940-0114-3
- Кемени Дж., Снелл Дж. Конечные цепи Маркова. — М. : Наука, 1970. — 272 c.
- Википедия — Цепь Маркова
- Wikipedia — Absorbing Markov chain