Дерево Фенвика — различия между версиями
Shersh (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 40 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
| + | == Описание структуры == | ||
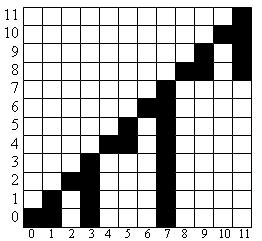
| + | [[Файл:Bit.jpg|thumb|300px|По горизонтали — индексы массива <tex>T</tex> <br/> (<tex>T_i</tex> является суммой элементов массива <tex>A</tex>, индексы которых заштрихованы),<br/> по вертикали — индексы массива <tex>A</tex>]] | ||
'''Дерево Фе́нвика''' (англ. ''Binary indexed tree'') — структура данных, требующая <tex> O(n) </tex> памяти и позволяющая эффективно (за <tex> O(\log n) </tex>) выполнять следующие операции: | '''Дерево Фе́нвика''' (англ. ''Binary indexed tree'') — структура данных, требующая <tex> O(n) </tex> памяти и позволяющая эффективно (за <tex> O(\log n) </tex>) выполнять следующие операции: | ||
* изменять значение любого элемента в массиве, | * изменять значение любого элемента в массиве, | ||
* выполнять некоторую [[Ассоциативная_операция |ассоциативную]], [[Абелева_группа |коммутативную]], [[Группа |обратимую операцию]] <tex> \circ </tex> на отрезке <tex> [i, j] </tex>. | * выполнять некоторую [[Ассоциативная_операция |ассоциативную]], [[Абелева_группа |коммутативную]], [[Группа |обратимую операцию]] <tex> \circ </tex> на отрезке <tex> [i, j] </tex>. | ||
| − | |||
Впервые описано Питером Фенвиком в 1994 году. | Впервые описано Питером Фенвиком в 1994 году. | ||
Пусть дан массив <tex> A = [a_0, a_1, ... , a_{n - 1}]</tex>. | Пусть дан массив <tex> A = [a_0, a_1, ... , a_{n - 1}]</tex>. | ||
| − | Деревом Фенвика будем называть массив <tex> T </tex> из <tex> n </tex> элементов: <tex> T_i = \sum\limits_{k = F(i)}^{i} a_k</tex>, где <tex> i = 0 .. n - 1 </tex> и <tex> F(i) </tex> — некоторая функция, от выбора которой зависит время работы операций над деревом. Рассмотрим функцию, позволяющую делать операции вставки и изменения элемента за время <tex> O(\log n) </tex>. Она задается простой формулой: <tex> F(i) = i \And (i + 1) </tex>, где <tex> \And </tex> — это операция логического <tex>AND</tex>. При <tex>AND</tex> числа и его значения, увеличенного на единицу, мы получаем это число без последних подряд идущих единиц. | + | Деревом Фенвика будем называть массив <tex> T </tex> из <tex> n </tex> элементов: <tex> T_i = \sum\limits_{k = F(i)}^{i} a_k</tex>, где <tex> i = 0 .. n - 1 </tex> и <tex> F(i) </tex> — некоторая функция, от выбора которой зависит время работы операций над деревом. Рассмотрим функцию, позволяющую делать операции вставки и изменения элемента за время <tex> O(\log n) </tex>. Она задается простой формулой: <tex> F(i) = i \And (i + 1) </tex>, где <tex> \And </tex> — это операция побитового логического <tex>AND</tex>. При <tex>AND</tex> числа и его значения, увеличенного на единицу, мы получаем это число без последних подряд идущих единиц. |
| + | |||
| + | Эту функцию можно вычислять по другой формуле: <tex> F(i) = i - 2^{h(i)} + 1, </tex> где <tex> h(i) </tex> — количество подряд идущих единиц в конце бинарной записи числа <tex> i </tex>. Оба варианта равносильны, так как функция, заданная какой-либо из этих формул, заменяет все подряд идущие единицы в конце числа на нули. | ||
== Запрос изменения элемента == | == Запрос изменения элемента == | ||
| Строка 13: | Строка 16: | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | Для | + | Для пересчёта дерева Фенвика при изменении величины <tex>a_{k}</tex> необходимо изменить элементы дерева <tex>T_{i}</tex>, для индексов <tex>i</tex> которых верно неравенство <tex>F(i) \leqslant k \leqslant i</tex> . |
|proof= | |proof= | ||
| − | <tex> T_i =\sum\limits_{k = F(i)}^{i} a_k , i = 0 .. n - 1 \Rightarrow</tex> необходимо менять те <tex> | + | <tex> T_i =\sum\limits_{k = F(i)}^{i} a_k , i = 0 .. n - 1 \Rightarrow</tex> необходимо менять те <tex>T_i</tex>, для которых <tex>a_{k}</tex> попадает в <tex>T_i \Rightarrow</tex> необходимые <tex> i </tex> удовлетворяют условию <tex>F(i) \leqslant k \leqslant i</tex>. |
}} | }} | ||
{{Лемма | {{Лемма | ||
| − | |statement= Все такие <tex> i </tex> | + | |statement= Все такие <tex> i </tex>, для которых меняется <tex>T_i</tex> при изменении <tex>a_k</tex>, можно найти по формуле <tex>i_{next} = i_{prev} \mid (i_{prev} + 1) </tex>, где <tex> \mid </tex> — это операция побитового логического <tex> OR </tex>. |
| − | |proof= | + | |proof=Из доказанной выше леммы следует, что первый элемент последовательности само <tex> k </tex>. Для него выполняется равенство, так как <tex> F(i) \leqslant i </tex>. По формуле <tex>i_{next} = i_{prev} \mid (i_{prev} + 1) </tex> мы заменим первый ноль на единицу. Неравенство при этом сохранится, так как <tex>F(i)</tex> осталось прежним или уменьшилось, а <tex> i </tex> увеличилось. <tex> F(i) </tex> не может увеличиться, так как функция <tex> F </tex> заменяет последние подряд идущие единицы числа <tex> i </tex> на нули, а по формуле <tex>i_{next} = i_{prev} \mid (i_{prev} + 1) </tex> у нового значения <tex> i </tex> увеличивается количество единиц в конце, что не может привести к увеличению <tex> F(i) </tex>. Докажем от противного, что нельзя рассматривать значения <tex> i </tex>, отличные от тех, которые мы получили по формуле. Рассмотрим две различные последовательности индексов. Первая последовательность получена по формуле, вторая — некоторая последовательность чисел превосходящих <tex>k</tex>. Возьмём число <tex> j </tex> из второй последовательности, которого нет в первой последовательности. Пусть <tex>F(j) \leqslant k </tex>. Уберём у <tex>j</tex> все подряд идущие единицы в конце двоичной записи, столько же цифр уберём в конце числа <tex>k</tex>. Обозначим их как <tex>j_{0}</tex> и <tex>k_{0}</tex>. Чтобы выполнялось условие <tex>F(j) \leqslant k </tex>, должно выполняться неравенство <tex>j_{0} \leqslant k_{0}</tex>. Но если <tex>j_{0} < k_{0}</tex>, то и <tex>j \leqslant k</tex>, что противоречит условию <tex>j > k</tex>. Значит, <tex>j_{0} = k_{0}</tex>. Но тогда <tex>j</tex> возможно получить по формуле <tex>i_{next} = i_{prev} \mid (i_{prev} + 1) </tex>, следовательно, <tex>F(j) > k </tex>. Получили противоречие: <tex>j</tex> можно вычислить по формуле, а это значит, что оно содержится в первой последовательности. Таким образом, нужные элементы можно искать по формуле <tex>i_{next} = i_{prev} \mid (i_{prev} + 1) </tex>. |
| − | + | }} | |
| − | + | ||
| + | Заметим, что <tex>F(i)</tex> возрастает немонотонно. Поэтому нельзя просто перебирать значения от <tex> k </tex>, пока не нарушается условие. Например, пусть <tex> k = 3 </tex>. При данной стратегии на следующем шаге (<tex> i = 4</tex>) нарушится условие и мы прекратим пересчитывать <tex> T_i </tex>. Но тогда мы упускаем остальные значения <tex>i</tex>, например <tex> 7 </tex>. | ||
{| style="background-color:#CCC;margin:0.5px" | {| style="background-color:#CCC;margin:0.5px" | ||
| − | |style="background-color:#EEE;padding:2px 30px"| <tex> | + | |style="background-color:#EEE;padding:3px 10px"| <tex>i</tex>, десятичная запись |
| − | |style="background-color:#FFF;padding:2px 30px"| <tex>\ | + | |style="background-color:#FFF;padding:3px 10px"| <tex>0</tex> |
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>1</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>2</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>3</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>4</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>5</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>6</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>7</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>8</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>9</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>10</tex> | ||
| + | |- | ||
| + | |style="background-color:#EEE;padding:3px 10px"| <tex>i</tex>, двоичная запись | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0001</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0010</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0011</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0100</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0101</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0110</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0111</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>1000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>1001</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>1010</tex> | ||
| + | |- | ||
| + | |style="background-color:#EEE;padding:3px 10px"| <tex>F(i)</tex>, двоичная запись | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0010</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0100</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0100</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0110</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>1000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>1000</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>1010</tex> | ||
| + | |- | ||
| + | |style="background-color:#EEE;padding:3px 10px"| <tex>F(i)</tex>, десятичная запись | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>2</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>4</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>4</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>6</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>0</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>8</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>8</tex> | ||
| + | |style="background-color:#FFF;padding:3px 10px"| <tex>10</tex> | ||
| + | |} | ||
| + | |||
| + | |||
| + | Все <tex>i</tex> мы можем получить следующим образом: <tex>i_{next} = i_{prev} \mid (i_{prev} + 1) </tex>. Следующим элементом в последовательности будет элемент, у которого первый с конца ноль превратится в единицу. Можно заметить, что если к исходному элементу прибавить единицу, то необходимый ноль обратится в единицу, но при этом все следующие единицы обнулятся. Чтобы обратно их превратить в единицы, применим операцию <tex>OR</tex>. Таким образом все нули в конце превратятся в единицы и мы получим нужный элемент. Для того, чтобы понять, что эта последовательность верна, достаточно посмотреть на таблицу. | ||
| + | |||
| + | {| style="background-color:#CCC;margin:0.5px" | ||
| + | |style="background-color:#EEE;padding:2px 30px"| <tex>i_{prev}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex>\ldots 011 \ldots 1</tex> | ||
|- | |- | ||
|style="background-color:#EEE;padding:2px 30px"| <tex>i_{prev} + 1</tex> | |style="background-color:#EEE;padding:2px 30px"| <tex>i_{prev} + 1</tex> | ||
| − | |style="background-color:#FFF;padding:2px 30px"| <tex>\ | + | |style="background-color:#FFF;padding:2px 30px"| <tex>\ldots 100 \ldots 0</tex> |
|- | |- | ||
|style="background-color:#EEE;padding:2px 30px"| <tex>i_{next}</tex> | |style="background-color:#EEE;padding:2px 30px"| <tex>i_{next}</tex> | ||
| − | |style="background-color:#FFF;padding:2px 30px"| <tex>\ | + | |style="background-color:#FFF;padding:2px 30px"| <tex>\ldots 111 \ldots 1</tex> |
|} | |} | ||
| + | Несложно заметить, что данная последовательность строго возрастает и в худшем случае будет применена логарифм раз, так как добавляет каждый раз по одной единице в двоичном разложении числа <tex>i</tex>. | ||
| − | + | Напишем функцию, которая будет прибавлять к элементу <tex>a_i</tex> число <tex>d</tex>, и при этом меняет соответствующие частичные суммы. Так как наш массив содержит <tex>N</tex> элементов, то мы будем искать <tex>i_{next}</tex> до тех пор, пока оно не превышает значение <tex>N</tex>. | |
| − | Напишем функцию, которая будет | ||
'''function''' modify(i, d): | '''function''' modify(i, d): | ||
| Строка 44: | Строка 105: | ||
i = i | (i + 1) | i = i | (i + 1) | ||
| − | + | Часто можно встретить задачу, где требуется заменить значение элемента <tex>a_i</tex> на <tex>x</tex>. Заметим, что если вычислить разность <tex>x</tex> и <tex>a_{i}</tex>, то можно свести эту задачу к операции прибавления <tex>d</tex> к <tex>a_i</tex>. | |
| − | |||
| − | |||
| − | {{ | + | '''function''' set(i, x): |
| − | + | d = x - a[i] | |
| − | }} | + | a[i] = x |
| − | + | modify(i, d) | |
| + | |||
| + | Построение дерева можно осуществить, исходя из его описания. Но можно быстрее, если использовать функцию <tex>\mathrm {modify}</tex> для каждого элемента массива <tex>A</tex>. Тогда мы получим время работы <tex>O(n \log {n})</tex>. | ||
| + | |||
| + | '''function''' build(): | ||
| + | '''for''' i = 0 '''to''' N - 1 | ||
| + | modify(i, a[i]) | ||
| + | |||
| + | == Запрос получения значения функции на префиксе == | ||
| + | Пусть существует некоторая бинарная операция <tex>\circ</tex>. Чтобы получить значение на отрезке <tex>[i, j]</tex>, нужно провести операцию, обратную к <tex>\circ</tex>, над значениями на отрезках <tex>[0, j]</tex> и <tex>[0, i - 1]</tex>. | ||
| + | |||
| + | В качестве бинарной операции <tex> \circ </tex> рассмотрим операцию сложения. | ||
| + | |||
| + | Обозначим <tex> G_i = \mathrm {sum(i)} = \sum\limits_{k = 0}^{i} a_k </tex>. Тогда <tex> \mathrm {sum(i, j)} = \sum\limits_{k = i}^{j} a_k = G_j - G_{i - 1} </tex>. | ||
| + | |||
| + | Для нахождения <tex>\mathrm {sum(i)}</tex> будем действовать следующим образом. Берём <tex>T_i</tex>, которое является суммой элементов с индексами от <tex>F(i)</tex> до <tex>i</tex>. Теперь к этому значению нужно прибавить <tex>\mathrm {sum(F(i) - 1)}</tex>. Аналогично продолжаем складывать, пока не <tex>F(i)</tex> не станет равным <tex>0</tex>. | ||
| + | |||
| + | Покажем, что запрос суммы работает за <tex>O(\log{n})</tex>. Рассмотрим двоичную запись числа <tex>i</tex>. Функция <tex>F(i)</tex> заменила его последние единицы на нули (заметим, что количество нулей в конце станет больше, чем количество единиц в конце до этого). Теперь вычтем единицу из <tex>F(i)</tex> (переход к следующему столбику). Количество единиц в конце увеличилось, по сравнению с <tex>i</tex>, так как мы заменили все нули в конце на единицы. Проводя эти действия дальше, мы придём к тому, что получили <tex>0</tex>. В худшем случае мы должны были повторять эти операции <tex>l</tex> раз, где <tex>l</tex> — количество цифр в двоичной записи числа <tex>i</tex>, что не превосходит <tex>\log_{2}{i} + 1</tex>. Значит, запрос суммы выполняется за <tex>O(\log{n})</tex>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Реализация === | === Реализация === | ||
| − | + | Приведем код функции <tex> \mathrm {sum(i)} </tex>: | |
| − | Приведем код функции <tex> \mathrm sum(i) </tex>: | ||
'''int''' sum(i): | '''int''' sum(i): | ||
| − | result = 0 | + | result = 0 |
'''while''' i >= 0 | '''while''' i >= 0 | ||
| − | result += t[i] | + | result += t[i] |
| − | i = f(i) - 1 | + | i = f(i) - 1 |
| − | + | return result | |
| − | == | + | ==Сравнение дерева Фенвика и дерева отрезков== |
| − | + | * Дерево Фенвика занимает в константное значение раз меньше памяти, чем дерево отрезков. Это следует из того, что дерево Фенвика хранит только значение операции для каких-то элементов, а дерево отрезков хранит сами элементы и частичные результаты операции на подотрезках, поэтому оно занимает как минимум в два раза больше памяти. | |
| − | + | * Дерево Фенвика проще в реализации. | |
| + | * Операция на отрезке, для которой строится дерево Фенвика, должна быть обратимой, а это значит, что минимум (как и максимум) на отрезке это дерево считать не может, в отличие от дерева отрезков. Но если нам требуется найти минимум на префиксе, то дерево Фенвика справится с этой задачей. Такое дерево Фенвика поддерживает операцию уменьшения элементов массива. Пересчёт минимума в дереве происходит быстрее, чем обновление массива минимумов на префиксе. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Дерево отрезков. Построение |Дерево отрезков]] | ||
==Источники информации== | ==Источники информации== | ||
* [http://citeseer.ist.psu.edu/viewdoc/download;jsessionid=F180153B9C0CD797594314B736E2CCC5?doi=10.1.1.14.8917&rep=rep1&type=pdf Peter M. Fenwick: A new data structure for cumulative frequency] | * [http://citeseer.ist.psu.edu/viewdoc/download;jsessionid=F180153B9C0CD797594314B736E2CCC5?doi=10.1.1.14.8917&rep=rep1&type=pdf Peter M. Fenwick: A new data structure for cumulative frequency] | ||
| − | * [http://en.wikipedia.org/wiki/Fenwick_tree Wikipedia — | + | * [http://en.wikipedia.org/wiki/Fenwick_tree Wikipedia — Fenwick tree] |
* [http://e-maxx.ru/algo/fenwick_tree Maximal:: algo:: Дерево Фенвика] | * [http://e-maxx.ru/algo/fenwick_tree Maximal:: algo:: Дерево Фенвика] | ||
| + | * [http://habrahabr.ru/post/112828 Хабрахабр — Дерево Фенвика] | ||
| Строка 88: | Строка 158: | ||
[[Категория: Дерево Фенвика]] | [[Категория: Дерево Фенвика]] | ||
| + | |||
| + | [[Категория: Структуры данных]] | ||
Текущая версия на 19:18, 4 сентября 2022
Содержание
Описание структуры
Дерево Фе́нвика (англ. Binary indexed tree) — структура данных, требующая памяти и позволяющая эффективно (за ) выполнять следующие операции:
- изменять значение любого элемента в массиве,
- выполнять некоторую ассоциативную, коммутативную, обратимую операцию на отрезке .
Впервые описано Питером Фенвиком в 1994 году.
Пусть дан массив . Деревом Фенвика будем называть массив из элементов: , где и — некоторая функция, от выбора которой зависит время работы операций над деревом. Рассмотрим функцию, позволяющую делать операции вставки и изменения элемента за время . Она задается простой формулой: , где — это операция побитового логического . При числа и его значения, увеличенного на единицу, мы получаем это число без последних подряд идущих единиц.
Эту функцию можно вычислять по другой формуле: где — количество подряд идущих единиц в конце бинарной записи числа . Оба варианта равносильны, так как функция, заданная какой-либо из этих формул, заменяет все подряд идущие единицы в конце числа на нули.
Запрос изменения элемента
Нам надо научиться быстро изменять частичные суммы в зависимости от того, как изменяются элементы. Рассмотрим как изменяется массив при изменении элемента .
| Лемма: |
Для пересчёта дерева Фенвика при изменении величины необходимо изменить элементы дерева , для индексов которых верно неравенство . |
| Доказательство: |
| необходимо менять те , для которых попадает в необходимые удовлетворяют условию . |
| Лемма: |
Все такие , для которых меняется при изменении , можно найти по формуле , где — это операция побитового логического . |
| Доказательство: |
| Из доказанной выше леммы следует, что первый элемент последовательности само . Для него выполняется равенство, так как . По формуле мы заменим первый ноль на единицу. Неравенство при этом сохранится, так как осталось прежним или уменьшилось, а увеличилось. не может увеличиться, так как функция заменяет последние подряд идущие единицы числа на нули, а по формуле у нового значения увеличивается количество единиц в конце, что не может привести к увеличению . Докажем от противного, что нельзя рассматривать значения , отличные от тех, которые мы получили по формуле. Рассмотрим две различные последовательности индексов. Первая последовательность получена по формуле, вторая — некоторая последовательность чисел превосходящих . Возьмём число из второй последовательности, которого нет в первой последовательности. Пусть . Уберём у все подряд идущие единицы в конце двоичной записи, столько же цифр уберём в конце числа . Обозначим их как и . Чтобы выполнялось условие , должно выполняться неравенство . Но если , то и , что противоречит условию . Значит, . Но тогда возможно получить по формуле , следовательно, . Получили противоречие: можно вычислить по формуле, а это значит, что оно содержится в первой последовательности. Таким образом, нужные элементы можно искать по формуле . |
Заметим, что возрастает немонотонно. Поэтому нельзя просто перебирать значения от , пока не нарушается условие. Например, пусть . При данной стратегии на следующем шаге () нарушится условие и мы прекратим пересчитывать . Но тогда мы упускаем остальные значения , например .
| , десятичная запись | |||||||||||
| , двоичная запись | |||||||||||
| , двоичная запись | |||||||||||
| , десятичная запись |
Все мы можем получить следующим образом: . Следующим элементом в последовательности будет элемент, у которого первый с конца ноль превратится в единицу. Можно заметить, что если к исходному элементу прибавить единицу, то необходимый ноль обратится в единицу, но при этом все следующие единицы обнулятся. Чтобы обратно их превратить в единицы, применим операцию . Таким образом все нули в конце превратятся в единицы и мы получим нужный элемент. Для того, чтобы понять, что эта последовательность верна, достаточно посмотреть на таблицу.
Несложно заметить, что данная последовательность строго возрастает и в худшем случае будет применена логарифм раз, так как добавляет каждый раз по одной единице в двоичном разложении числа .
Напишем функцию, которая будет прибавлять к элементу число , и при этом меняет соответствующие частичные суммы. Так как наш массив содержит элементов, то мы будем искать до тех пор, пока оно не превышает значение .
function modify(i, d):
while i < N
t[i] += d
i = i | (i + 1)
Часто можно встретить задачу, где требуется заменить значение элемента на . Заметим, что если вычислить разность и , то можно свести эту задачу к операции прибавления к .
function set(i, x): d = x - a[i] a[i] = x modify(i, d)
Построение дерева можно осуществить, исходя из его описания. Но можно быстрее, если использовать функцию для каждого элемента массива . Тогда мы получим время работы .
function build():
for i = 0 to N - 1
modify(i, a[i])
Запрос получения значения функции на префиксе
Пусть существует некоторая бинарная операция . Чтобы получить значение на отрезке , нужно провести операцию, обратную к , над значениями на отрезках и .
В качестве бинарной операции рассмотрим операцию сложения.
Обозначим . Тогда .
Для нахождения будем действовать следующим образом. Берём , которое является суммой элементов с индексами от до . Теперь к этому значению нужно прибавить . Аналогично продолжаем складывать, пока не не станет равным .
Покажем, что запрос суммы работает за . Рассмотрим двоичную запись числа . Функция заменила его последние единицы на нули (заметим, что количество нулей в конце станет больше, чем количество единиц в конце до этого). Теперь вычтем единицу из (переход к следующему столбику). Количество единиц в конце увеличилось, по сравнению с , так как мы заменили все нули в конце на единицы. Проводя эти действия дальше, мы придём к тому, что получили . В худшем случае мы должны были повторять эти операции раз, где — количество цифр в двоичной записи числа , что не превосходит . Значит, запрос суммы выполняется за .
Реализация
Приведем код функции :
int sum(i):
result = 0
while i >= 0
result += t[i]
i = f(i) - 1
return result
Сравнение дерева Фенвика и дерева отрезков
- Дерево Фенвика занимает в константное значение раз меньше памяти, чем дерево отрезков. Это следует из того, что дерево Фенвика хранит только значение операции для каких-то элементов, а дерево отрезков хранит сами элементы и частичные результаты операции на подотрезках, поэтому оно занимает как минимум в два раза больше памяти.
- Дерево Фенвика проще в реализации.
- Операция на отрезке, для которой строится дерево Фенвика, должна быть обратимой, а это значит, что минимум (как и максимум) на отрезке это дерево считать не может, в отличие от дерева отрезков. Но если нам требуется найти минимум на префиксе, то дерево Фенвика справится с этой задачей. Такое дерево Фенвика поддерживает операцию уменьшения элементов массива. Пересчёт минимума в дереве происходит быстрее, чем обновление массива минимумов на префиксе.