Автомат Кнута-Морриса-Пратта — различия между версиями
YanaZimka (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 3 промежуточные версии 3 участников) | |||
| Строка 62: | Строка 62: | ||
'''if''' q > 0 '''and''' a <tex>\ne</tex> p[q + 1] | '''if''' q > 0 '''and''' a <tex>\ne</tex> p[q + 1] | ||
<tex>\delta</tex>(q, a) = <tex>\delta</tex>(<tex>\pi_p</tex>(q), a) | <tex>\delta</tex>(q, a) = <tex>\delta</tex>(<tex>\pi_p</tex>(q), a) | ||
| − | '''if''' | + | '''if''' a = p[q + 1] |
<tex>\delta</tex>(q, a) = q + 1 | <tex>\delta</tex>(q, a) = q + 1 | ||
'''else''' | '''else''' | ||
| Строка 86: | Строка 86: | ||
[[Категория: Поиск подстроки в строке]] | [[Категория: Поиск подстроки в строке]] | ||
[[Категория: Автоматы и регулярные языки]] | [[Категория: Автоматы и регулярные языки]] | ||
| + | [[Категория:Точный поиск]] | ||
Текущая версия на 19:19, 4 сентября 2022
Автомат Кнута-Морриса-Пратта используется в алгоритмах, связанных с поиском образца в тексте, в том числе в реальном времени.
Содержание
Суффикс-функция
| Определение: |
| Для строки длиной функция называется суффикс-функцией, если она сопоставляет любой строке , состоящей из символов алфавита , длину максимального суффикса , являющегося префиксом . |
Пример суффикс-функции
Пусть строка ="". Вот несколько примеров значений суффикс-функции для нее.
- .
- В данном случае вся строка является префиксом .
- .
- В данном случае какой бы суффикс мы ни взяли, ни один из них не является префиксом .
- .
- В данном случае "" является префиксом , а все суффиксы длиннее — нет.
Структура автомата
Автомат строится на строке-образце длины , которую в будущем мы будем искать в тексте.
Для автомата Кнута-Морриса-Пратта:
- , где — это состояние, — символ, по которому осуществляется переход, a "" — операция конкатенации ().
Таким образом, если часть текста, в котором мы ищем образец, уже пропущена через автомат, то текущее состояние отражает, сколько последних символов этой прочитанной части совпадает с началом нашего образца. Если мы пришли в допускающее состояние, значит последние символов полностью совпадают с образцом и мы нашли включение.
Заметим, что тот факт, что переход по символу осуществляется независимо от последующих, позволяет нам работать как с текстом, данным заранее, так и с текстом, который вводится в реальном времени.
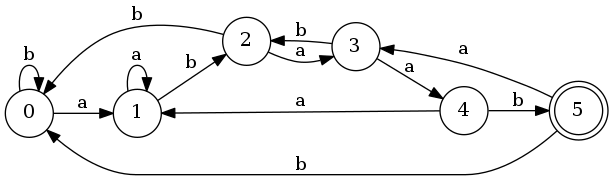
Пример автомата Кнута-Морриса-Пратта
Данный автомат построен для образца "" и алфавита
Построение автомата
Идея алгоритма
Для каждого состояния и каждого символа будем определять значение функции перехода из данного состояния по данному символу. Пусть текущее состояние . При считывании каждого нового символа из текста возможно два варианта развития событий:
- Это значит, что число последних символов текста, совпадающих с началом образца увеличилось на 1. Значит переход осуществляется в следующее состояние. В этом случае .
- Тогда заметим, что если к строке, являющейся максимальным бордером предыдущего совпадения, добавить прочитанный символ, то как раз получится текущее окончание текста, совпадающее с началом образца. Таким образом, в этом случае , где — префикс-функция для строки . Исключением для этого случая является лишь нулевое состояние. Если считанный символ не совпадает с первым символом образца, то мы останемся в нулевом состоянии, так как по прежнему совпадением является пустая строка.
Асимптотика
В данном алгоритме нам нужно лишь вычислить значение функции перехода в каждом состоянии для каждого символа. При предподсчитанной за префикс-функции вычисление для одного состояния и одного символа происходит за . Всего состояний , а символов . Итого .
Псевдокод
function make_kmp()
for q = 0 to m
for a
if q > 0 and a p[q + 1]
(q, a) = ((q), a)
if a = p[q + 1]
(q, a) = q + 1
else
(q, a) = q
Сравнение с другими алгоритмами поиска образца в тексте
При решении задачи поиска всех включений образца в текст также часто применяются алгоритмы Ахо-Корасик и Кнута-Морриса-Пратта.
Алгоритм Ахо-Корасик использует автомат, построенный на основе приведенного здесь, и является расширением рассматриваемого алгоритма. Он применяется в несколько иных случаях — когда образцов для поиска несколько. И решает эту задачу быстрее, чем построение нескольких автоматов Кнута-Морриса-Пратта.
Алгоритм Кнута-Морриса-Пратта решает ту же задачу, что и алгоритм с применением одноименного автомата. Однако он не может работать с текстом, вводимым в режиме реального времени, ему нужно заранее знать текст, в котором нужно искать образец. Также, если текст достаточно объемный, алгоритм Кнута-Морриса-Пратта будет использовать гораздо больше памяти, чем приведенный выше в данной статье. Однако, если текст небольшой и дан заранее, алгоритм Кнута-Морриса-Пратта будет работать быстрее.
См. также
Источники информации
- Wikipedia — Finite-state machine
- ISBN 978-5-8459-1794-2 Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн — Алгоритмы. Построение и анализ, стр. 771—776.